# 網路最大流 #### 目錄 - 前言 - 雙倍經驗 - 網路流初步 - 網路最大流 - $EK$增廣路演算法 - $Dinic$演算法 ------------ #### 前言 這篇題解是當做學習記錄寫的，所以會對網路最大流這個概念進行講解（$dalao$們可以忽略蒟蒻$orz$） #### 雙倍經驗$Time$ 1. [洛谷P3376 【模板】](https://www.luogu.com.cn/problem/P3376) （$Ek$演算法 / $Dinic$演算法） 2. [洛谷P2740 [USACO4.2]草地排水Drainage Ditches](https://www.luogu.com.cn/problem/P2740) ------------ #### 網路流初步 這裡主要討論一下網路流演算法可能會涉及到的一些概念性問題 - 定義 對於任意一張**有向圖**（也就是**網路**），其中有$N$個點、$M$條邊以及源點$S$和匯點$T$ 然後我們把$c(x,y)$稱為邊的**容量** - 轉換 為了通俗易懂，我們來結合生活實際理解上面網路的定義： 將有向圖理解為我們城市的**水網**，有$N$戶家庭、$M$條管道以及供水點$S$和匯合點$T$ 是不是好理解一點？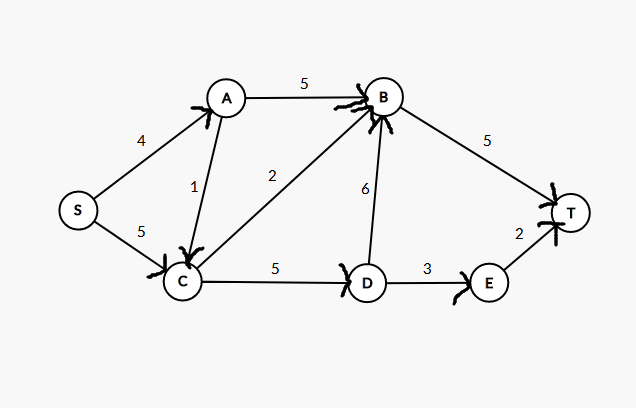現在給出一張網路（圖醜勿怪啊QAQ）：  $S->C->D->E->T$就是該網路的一個流，$2$這個流的流量 - 流函式 和上面的$c$差不多，我們把$f(x,y)$稱為邊的**流量**，則$f$稱為網路的流函式，它滿足三個條件： 1. $s(x,y)≤c(x,y)$ 2. $f(x,y)=-f(y,x)$ 3. $\forall$ $x$≠$S$，$x≠T$, $\sum_{(u,x)∈E }f(u,x)=\sum_{(x,v)∈E }f(x,v)$ 這三個條件其實也是流函式的三大性質： 1. 容量限制：每條邊的流量總不可能大於該邊的容量的（不然水管就爆了） 2. 斜對稱：正向邊的流量=反向邊的流量（反向邊後面會具體講） 3. 流量守恆：正向的所有流量和=反向的所有流量和（就是總量始終不變） - 殘量網路 在任意時刻，網路中所有節點以及剩餘容量大於$0$的邊構成的子圖被稱為**殘量網路** ------------ #### 最大流 對於上面的網路，合法的流函式有很多，其中使得整個網路流量之和最大的流函式稱為網路的**最大流**，此時的流量和被稱為網路的**最大流量** 最大流能解決許多實際問題，比如：一條完整運輸道路（含多條管道）的一次最大運輸流量，還有**二分圖**（蒟蒻還沒學二分圖，學了之後會更新的qwq） 下面就來介紹計算最大流的兩種演算法：$EK$增廣路演算法和$Dinic$演算法 ------------ #### $Edmonds-Karp$增廣路演算法 （為了簡便，習慣稱為$EK$演算法） - 首先來講增廣路是什麼： 若一條從$S$到$T$的路徑上所有邊的剩餘容量都大於0，則稱這樣的路徑為一條**增廣路**（剩餘流量：$c(x,y)-f(x,y)$） - 然後就是$EK$演算法的核心思想啦： 如上，顯然我們可以讓一股流沿著增廣路從$S$流到$T$，然後使網路的流量增大 $EK$演算法的思想就是**不斷用**BFS**尋找增廣路並不斷更新最大流量值，直到網路上不存在增廣路為止** - 再來講理論實現過程： 在$BFS$尋找一條增廣路時，我們只需要考慮**剩餘流量不為$0$的邊**，然後找到一條從$S$到$T$的路徑，同時計算出路徑上**各邊剩餘容量值的最小值$dis$**，則網路的最大流量就可以增加$dis$（**經過的正向邊容量值全部減去$dis$，反向邊全部加上$dis$**） - **反向邊** 插入講解一下反向邊這個概念，這是網路流中的一個重點 為什麼要建反向邊？ 因為可能**一條邊可以被包含於多條增廣路徑**，所以為了尋找所有的增廣路經我們就要讓這一條邊有**多次被選擇的機會** 而構建反向邊則是這樣一個機會，相當於給程式一個**反悔**的機會！ 為什麼是反悔？ 因為我們在找到一個$dis$後，就會對每條邊的容量進行減法操作，而**直接更改值就會影響到之後尋找另外的增廣路**！ 還不好理解？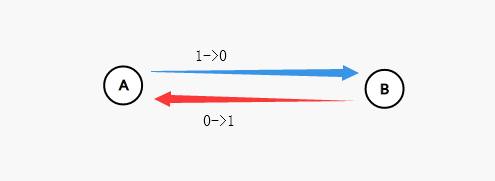那我們舉個~~通俗易懂的~~例子吧：  原本$A$到$B$的正邊權是1、反邊權是0，在第一次經過該邊後（假設$dis$值為1），則正邊權變為0，反邊權變為1 當我們需要第二次經過該邊時，我們就能夠通過走反向邊恢復這條邊的原樣（可能有點繞，大家好好理解一下） 以上都是我個人的理解，現在給出《演算法競賽進階指南》上關於反向邊的證明： “**當一條邊的流量$f(x,y)>0$時，根據斜對稱性質，它的反向邊流量$f(y,x)<0$，此時必定有$f(y,x)

using namespace std; int n,m,s,t,u,v; long long w,ans,dis[520010]; int tot=1,vis[520010],pre[520010],head[520010],flag[2510][2510]; struct node { int to,net; long long val; } e[520010]; inline void add(int u,int v,long long w) { e[++tot].to=v; e[tot].val=w; e[tot].net=head[u]; head[u]=tot; e[++tot].to=u; e[tot].val=0; e[tot].net=head[v]; head[v]=tot; } inline int bfs() { //bfs尋找增廣路 for(register int i=1;i<=n;i++) vis[i]=0; queue q; q.push(s); vis[s]=1; dis[s]=2005020600; while(!q.empty()) { int x=q.front(); q.pop(); for(register int i=head[x];i;i=e[i].net) { if(e[i].val==0) continue; //我們只關心剩餘流量>0的邊 int v=e[i].to; if(vis[v]==1) continue; //這一條增廣路沒有訪問過 dis[v]=min(dis[x],e[i].val); pre[v]=i; //記錄前驅，方便修改邊權 q.push(v); vis[v]=1; if(v==t) return 1; //找到了一條增廣路 } } return 0; } inline void update() { //更新所經過邊的正向邊權以及反向邊權 int x=t; while(x!=s) { int v=pre[x]; e[v].val-=dis[t]; e[v^1].val+=dis[t]; x=e[v^1].to; } ans+=dis[t]; //累加每一條增廣路經的最小流量值 } int main() { scanf("%d%d%d%d",&n,&m,&s,&t); for(register int i=1;i<=m;i++) { scanf("%d%d%lld",&u,&v,&w); if(flag[u][v]==0) { //處理重邊的操作（加上這個模板題就可以用Ek演算法過了） add(u,v,w); flag[u][v]=tot; } else { e[flag[u][v]-1].val+=w; } } while(bfs()!=0) { //直到網路中不存在增廣路 update(); } printf("%lld",ans); return 0; } ``` ------------ #### $Dinic$演算法 $EK$演算法每次都可能會遍歷整個殘量網路，但只找出一條增廣路 是不是有點不划算？能不能一次找多條增廣路呢？ 答案是可以的：$Dinic$演算法 - 分層圖&$DFS$ 根據$BFS$寬度優先搜尋，我們知道對於一個節點$x$，我們用$d[x]$來表示它的**層次**，即$S$到$x$最少需要經過的邊數。在殘量網路中，滿足$d[y]=d[x]+1$的邊$(x,y)$構成的子圖被稱為**分層圖**（相信大家已經接觸過了吧），而分層圖很明顯是一張有向無環圖 為什麼要建分層圖？ 講這個原因之前， 我們還要知道一點：**$Dinic$演算法還需要$DFS$** 現在再放上第一張圖，我們來理解  根據層次的定義，我們可以得出： ``` 第0層：S 第1層：A、C 第2層：B、D 第3層：E、T ``` 在$DFS$中，從$S$開始，每次我們向下一層次隨便找一個點，直到到達$T$，然後再一層一層回溯回去，繼續找這一層的另外的點再往下搜尋 這樣就滿足了我們同時求出多條增廣路的需求！ - $Dinic$演算法框架 1. 在殘量網路上$BFS$求出節點的層次，構造分層圖 2. 在分層圖上$DFS$尋找增廣路，在回溯時同時更新邊權 - 適用範圍 時間複雜度：$O(n^2m)$，一般能夠處理$10^4$~$10^5$規模的網路 相較於$EK$演算法，顯然$Dinic$演算法的效率更優也更快：雖然在稀疏圖中區別不明顯，但在稠密圖中$Dinic$的優勢便凸顯出來了（所以$Dinic$演算法用的更多） 此外，$Dinic$演算法求解二分圖最大匹配的時間複雜度為$O(m\sqrt{n})$ - 程式碼$Code$ 這份程式碼是本模板題的AC程式碼，但是使用到了$Dinic$演算法的兩個優化：**當前弧優化+剪枝** ```cpp #include

using namespace std; const long long inf=2005020600; int n,m,s,t,u,v; long long w,ans,dis[520010]; int tot=1,now[520010],head[520010]; struct node { int to,net; long long val; } e[520010]; inline void add(int u,int v,long long w) { e[++tot].to=v; e[tot].val=w; e[tot].net=head[u]; head[u]=tot; e[++tot].to=u; e[tot].val=0; e[tot].net=head[v]; head[v]=tot; } inline int bfs() { //在慘量網路中構造分層圖 for(register int i=1;i<=n;i++) dis[i]=inf; queue q; q.push(s); dis[s]=0; now[s]=head[s]; while(!q.empty()) { int x=q.front(); q.pop(); for(register int i=head[x];i;i=e[i].net) { int v=e[i].to; if(e[i].val>0&&dis[v]==inf) { q.push(v); now[v]=head[v]; dis[v]=dis[x]+1; if(v==t) return 1; } } } return 0; } inline int dfs(int x,long long sum) { //sum是整條增廣路對最大流的貢獻 if(x==t) return sum; long long k,res=0; //k是當前最小的剩餘容量 for(register int i=now[x];i&∑i=e[i].net) { now[x]=i; //當前弧優化 int v=e[i].to; if(e[i].val>0&&(dis[v]==dis[x]+1)) { k=dfs(v,min(sum,e[i].val)); if(k==0) dis[v]=inf; //剪枝，去掉增廣完畢的點 e[i].val-=k; e[i^1].val+=k; res+=k; //res表示經過該點的所有流量和（相當於流出的總量） sum-=k; //sum表示經過該點的剩餘流量 } } return res; } int main() { scanf("%d%d%d%d",&n,&m,&s,&t); for(register int i=1;i<=m;i++) { scanf("%d%d%lld",&u,&v,&w); add(u,v,w); } while(bfs()) { ans+=dfs(s,inf); //流量守恆（流入=流出） } printf("%lld",ans); return 0; } ``` - **當前弧優化** 對於一個節點$x$，當它在$DFS$中走到了第$i$條弧時，前$i-1$條弧到匯點的流一定已經被流滿而沒有可行的路線了 那麼當下一次再訪問$x$節點時，前$i-1$條弧就沒有任何意義了 所以我們可以在每次列舉節點$x$所連的弧時，改變列舉的起點，這樣就可以刪除起點以前的所有弧，來達到優化剪枝的效果 對應到程式碼中，就是$now$陣列 ------------ #### 後序 終於寫完了....現在來特別感謝一些：@那一條變阻器 對於使用$EK$演算法過掉本題的幫助 以及 @取什麼名字 講解$Dinic$演算法的$DFS$部分內容 如果本篇題解有任何錯誤或您有任何不懂的地方，歡迎留言區評論，我會及時回覆、更正，謝謝大家orz！ -----