word2vec是google 2013年提出的，從大規模語料中訓練詞向量的模型，在許多場景中都有應用，資訊提取相似度計算等等。也是從word2vec開始，embedding在各個領域的應用開始流行，所以拿word2vec來作為開篇再合適不過了。本文希望可以較全面的給出Word2vec從模型結構概述，推導，訓練，和基於tf.estimator實現的具體細節。完整程式碼戳這裡https://github.com/DSXiangLi/Embedding ## 模型概述 word2vec模型結構比較簡單，是為了能夠在大規模資料上訓練，降低了模型複雜度，移除了非線性隱藏層。根據不同的輸入輸出形式又分成CBOW和SG兩種方法。 讓我們先把問題簡化成1v1的bigram問題，單詞i作為context,單詞j是target。V是單詞總數，N是詞向量長度，D是訓練詞對，輸入$x_i \in R ^{1*V}$是one-hot向量。

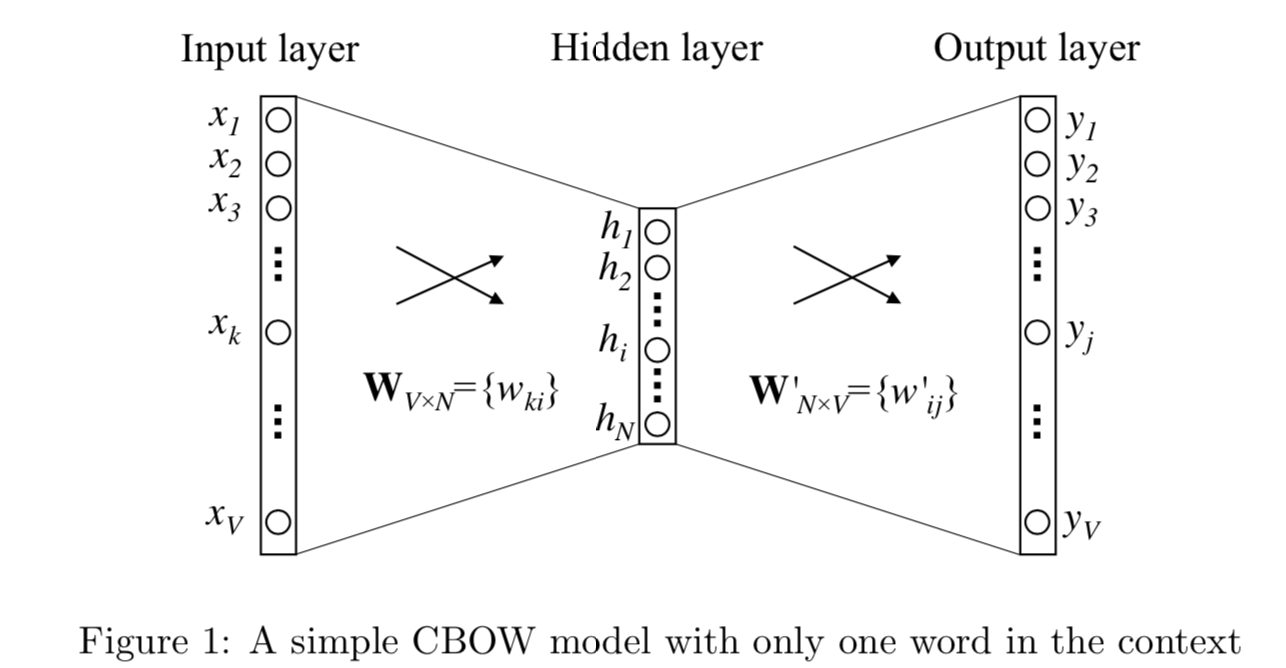
模型訓練兩個權重矩陣,$W \in R ^{V*N}$是輸入矩陣，每一行對應輸入單詞的詞向量,$W^{'} \in R ^{V*N}$是輸出矩陣，每一行對應輸出單詞的詞向量。詞i和詞j的共現資訊用詞向量的內積來表達，通過softmax得到每個單詞的概率如下 $$ \begin{align} h =v_{wI} &= W^T x_i \\ v_{w^{'}j} &= W^{'T} x_j \\ u_j &= v_{w^{'}j}^T h \\ y_j = p(w_j|w_I) &= \frac{exp(u_j)}{\sum_{j^{'}=1}^Vexp(u_{j^{'}})}\\ \end{align} $$ 對每個訓練樣本，模型的目標是最大化條件概率$p(w_j|w_I)$, 因此我們的對數損失函式如下 $$ \begin{align} E & = - logP(w_j|w_I) \\ & = -u_j^* + log\sum_{j^{'}=1}^Vexp(u_{j^{'}}) \end{align} $$ ### CBOW : Continuous bag of words CBOW是把bigram的輸入context，擴充套件成了目標單詞周圍2*window_size內的單詞，用中心詞前後的語境來預測中心詞。

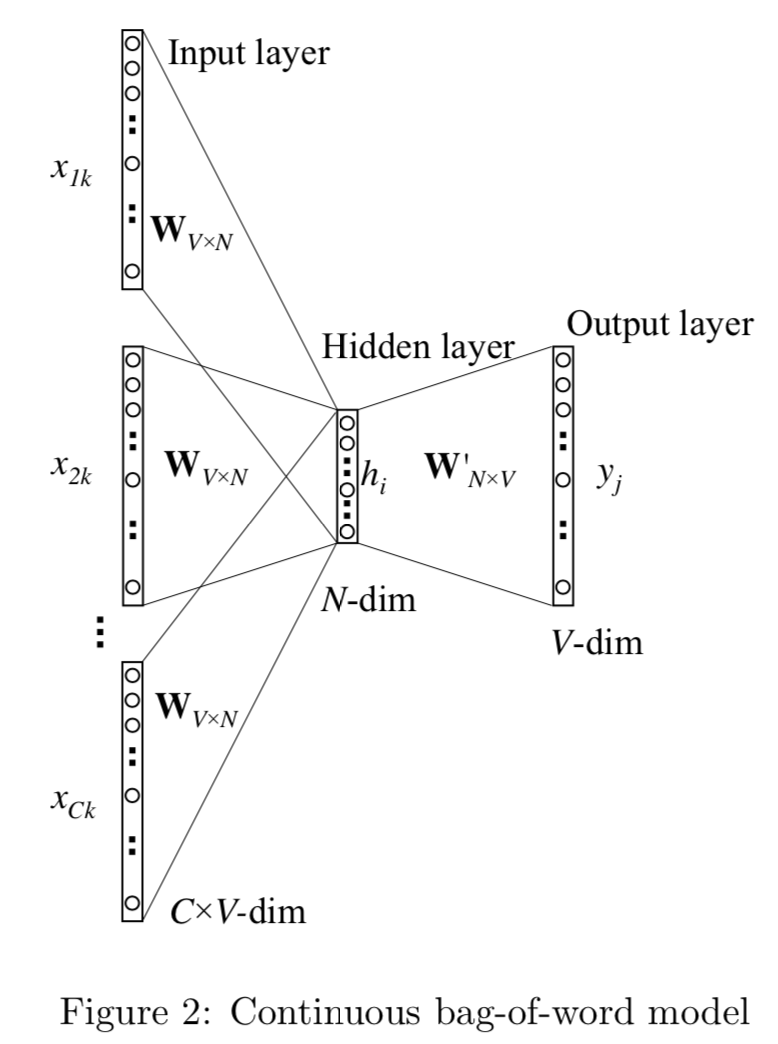
對比bigram, CBOW只多做了一步操作，對輸入的2 * Window_size個單詞，在對映得到詞向量後，需要做average_pooling得到1*N的輸入向量, 所以差異只在h的計算。假定$C = 2 * \text{window_size}$ $$ \begin{align} h & = \frac{1}{C}W^T(x_1 + x_2 +... + x_C) \\ & = \frac{1}{C}(v_{w1} + v_{w2} + ... + v_{wc}) ^T \\ E &= -log \, p(w_O|w_{I,1}...w_{I,C}) \\ & = -u_j^* + log\sum_{j^{'}=1}^Vexp(u_{j^{'}}) \end{align} $$ ### SG : Skip Gram SG是把bigram的輸出target，擴充套件成了輸入單詞周圍2*window_size內的單詞，用中心詞來預測周圍單詞的出現概率。

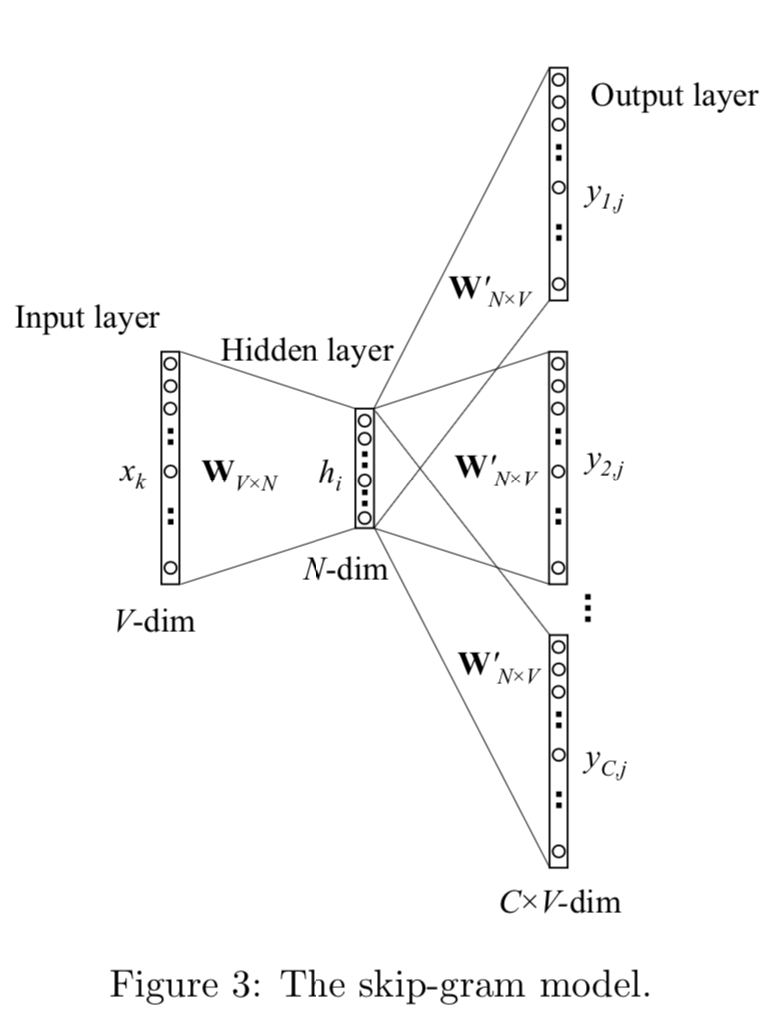
對比bigram，SG的差異只在於輸出概率多項分佈不再是一個而是C個 $$ \begin{align} E &= -log \, p(w_{O,1},w_{O,2},...w_{O,C}|w_I) \\ & =\sum_{c=1}^Cu_{j,c}^* + C\cdot log\sum_{j^{'}=1}^Vexp(u_{j^{'}}) \end{align} $$ ## 模型推導：word embedding是如何得到的？ 下面我們從back propogation推導下以上模型結構是如何學到詞向量的，為簡化我們還是先從bigram來看，$\eta$是learning rate。 首先是hidden->output $W^{'}$的詞向量的更新 $$ \begin{align} \frac{\partial E}{\partial v_{w^{'}j}} &= \frac{\partial E}{\partial u_j}\frac{\partial u_j}{\partial v_{w^{'}j}}\\ & = (p(w_j|w_i) - I(j=j^*))\cdot h \\ & = e_j\cdot h \\ v_{w^{'}j}^{(new)} &= v_{w^{'}j}^{(old)} - \eta \cdot e_j \cdot h \\ \end{align} $$ $e_j$是單詞j的預測概率誤差，所以$W^{'}$的更新可以理解為如果單詞j被高估就從$v_{w^{'}j}$中減去$\eta \cdot e_j \cdot h$，降低h和$v_{w^{'}j}$的向量內積(similarity)，反之被低估則在$v_{w^{'}j}$上疊加$\eta \cdot e_j \cdot h$增加內積相似度，誤差越大更新的幅度越大。 然後是input->hidden W的詞向量的更新 $$ \begin{align} \frac{\partial E}{\partial h} &= \sum_{j=1}^V\frac{\partial E}{\partial u_j}\frac{\partial u_j}{\partial h}\\ & = \sum_{j=1}^V e_j \cdot v_{w^{'}j}\\ v_{w_I}^{(new)} &= v_{w_I}^{(old)} - \eta \cdot \sum_{j=1}^V e_j \cdot v_{w^{'}j} \\ \end{align} $$ 每個輸入單詞對應的詞向量$v_{wI}$，都用所有單詞的輸出詞向量按預測誤差加權平均得到的向量進行更新。和上述的邏輯相同高估做subtraction，低估的做addition然後按誤差大小進行加權來更新輸入詞向量。 所以模型學習過程會是輸入詞向量更新輸出詞向量，輸出詞向量再更新輸入詞向量，然後back-and-forth到達穩態。 把bigram拓展到CBOW，唯一的變化在於更新input-hidden的詞向量時，不是每次更新一個單詞對應的向量，而是用相同的幅度同時更新C個單詞的詞向量. $$ v_{w_{I,c}}^{(new)} = v_{w_{I,c}}^{(old)} - \frac{1}{C}\eta \cdot \sum_{j=1}^V e_j \cdot v_{w^{'}j} $$ 把bigram拓展到SG，唯一的變化在於更新hidden-output的詞向量時，不再是用單詞j的預測誤差，而是用C個單詞的預測誤差之和 $$ v_{w^{'}j}^{(new)} = v_{w^{'}j}^{(old)} - \eta \cdot \sum_{c=1}^C e_{c,j} \cdot h $$ ## 模型訓練 雖然模型結構已經做了優化，移除了非線性的隱藏層，但是模型訓練起來並不高效,瓶頸在於Word2vec本質是多分類任務，類別有整個vocabulary這麼多，所以$p(w_j|w_I) = \frac{exp(u_j)}{\sum_{j^{'}=1}^Vexp(u_{j^{'}})}$每次需要計算整個vocabulary的概率$O(VN)$。即便batch只有1個訓練樣本，也需要更新所有單詞hidden->output的embedding矩陣。針對這個問題有兩種解決方案 ### Hierarchical Softmax 如果把softmax看作一個1-layer tree,每個單詞都是一個葉節點, 因為需要歸一化所以計算每個單詞的概率的複雜度是$O(V)$。Hierarchical Softmax只是把1-layer變成了multi-layer，在不增加embedding大小的情況下（V個葉節點，樹有V-1個inner node), 把計算每個單詞概率的複雜度降低到$O(logV)$，直接用從root到葉節點的路徑來計算每個單詞的概率。樹的構造作者選用了huffman tree,優點在於高頻詞從root到leaf的路徑會比低頻詞更短，這樣可以進一步加速訓練，具體細節可以來看這篇部落格[human coding][1] 例如下圖（[圖片來源][2]）

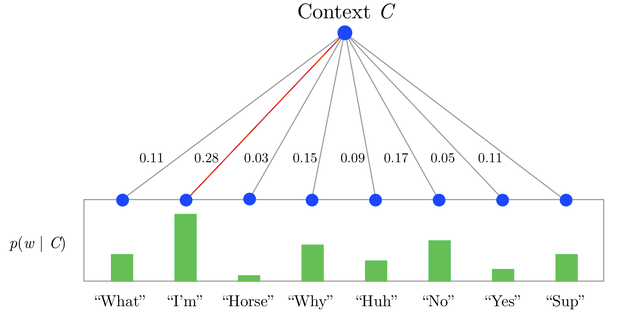
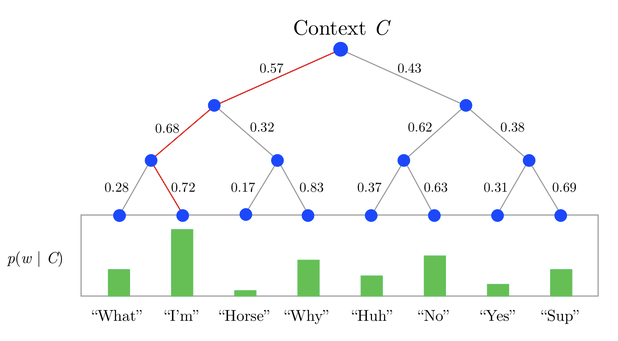
$$ \begin{align} P(Horse) &= P(0,left)\cdot P(1,right)\cdot P(2,left) \end{align} $$ 那具體上面的p(0,left)要如何計算呢？ 每一個node都有自己的embedding $v_n{(w,j)}$, 既單詞w路徑上第j個node的embedding,輸入輸出的單詞內積，變為輸入單詞和node的內積， 每個單詞的概率計算如下 $$ p(w=w_o) = \prod_{j=1}^{L(w)-1}\sigma([n(w,j+1) = ch(n(w,j))] \cdot {v_{n(w,j)}}^{T} h) $$ 不得不說這個式子寫的真是生怕別人能看懂>_< $[n(w,j+1) = ch(n(w,j))]$ 是個啥？ch是left child，$[\cdot]$只是用來判斷path是往左還是往右 $$ \ [\cdot] = \begin{cases} 1 & \quad \text{if 往左} \\ -1 & \quad \text{if 往右} \end{cases} \ $$ 所以 $$ \begin{align} p(n,left) &= \sigma(v_n^T\cdot h )\\ p(n, right) &= \sigma(-v_n^T\cdot h )= 1- \sigma(v_n^T\cdot h ) \end{align} $$ 對應上面的模型推導，hidden->ouput的部分發生變化, 損失函式變為以下 $$ E= -log P(w=w_j|w_I) = - \sum_{j=1}^{L(w)-1}log([\cdot]v_j^T h) $$ 每次output單詞對應的路徑上的embedding會被更新，預測任務變為該路徑上每個inner_node應該往左還是往右。 簡單的huffman Hierarchy softmax的實現如下 ```python class TreeNode(object): total_node = 0 def __init__(self, frequency, char = None , word_index = None, is_leaf = False): self.frequency = frequency self.char = char # word character self.word_index = word_index # word look up index self.left = None self.right = None self.is_leaf = is_leaf self.counter(is_leaf) def counter(self, is_leaf): # node_index will be used for embeeding_lookup self.node_index = TreeNode.total_node if not is_leaf: TreeNode.total_node += 1 def __lt__(self, other): return self.frequency < other.frequency def __repr__(self): if self.is_leaf: return 'Leaf Node char = [{}] index = {} freq = {}'.format(self.char, self.word_index, self.frequency) else: return 'Inner Node [{}] freq = {}'.format(self.node_index, self.frequency) class HuffmanTree(object): def __init__(self, freq_dic): self.nodes = [] self.root = None self.max_depth = None self.freq_dic = freq_dic self.all_paths = {} self.all_codes = {} self.node_index = 0 @staticmethod def merge_node(left, right): parent = TreeNode(left.frequency + right.frequency) parent.left = left parent.right = right return parent def build_tree(self): """ Build huffman tree with word being leaves """ TreeNode.total_node = 0 # avoid train_and_evaluate has different node_index heap_nodes = [] for word_index, (char, freq) in enumerate(self.freq_dic.items()): tmp = TreeNode( freq, char, word_index, is_leaf=True ) heapq.heappush(heap_nodes, tmp ) while len(heap_nodes)>1: node1 = heapq.heappop(heap_nodes) node2 = heapq.heappop(heap_nodes) heapq.heappush(heap_nodes, HuffmanTree.merge_node(node1, node2)) self.root = heapq.heappop(heap_nodes) @property def num_node(self): return self.root.node_index + 1 def traverse(self): """ Compute all node to leaf path and direction: list of node_id, list of 0/1 """ def dfs_helper(root, path, code): if root.is_leaf : self.all_paths[root.word_index] = path self.all_codes[root.word_index] = code return if root.left : dfs_helper(root.left, path + [root.node_index], code + [0]) if root.right : dfs_helper(root.right, path + [root.node_index], code + [1]) dfs_helper(self.root, [], [] ) self.max_depth = max([len(i) for i in self.all_codes.values()]) class HierarchySoftmax(HuffmanTree): def __init__(self, freq_dic): super(HierarchySoftmax, self).__init__(freq_dic) def convert2tensor(self): # padded to max_depth and convert to tensor with tf.name_scope('hstree_code'): self.code_table = tf.convert_to_tensor([ code + [INVALID_INDEX] * (self.max_depth - len(code)) for word, code in sorted( self.all_codes.items(), key=lambda x: x[0] )], dtype = tf.float32) with tf.name_scope('hstree_path'): self.path_table = tf.convert_to_tensor([path + [INVALID_INDEX] * (self.max_depth - len(path)) for word, path in sorted( self.all_paths.items(), key=lambda x: x[0] )], dtype = tf.int32) def get_loss(self, input_embedding_vector, labels, output_embedding, output_bias, params): """ :param input_embedding_vector: [batch * emb_size] :param labels: word index [batch * 1] :param output_embedding: entire embedding matrix [] :return: loss """ loss = [] labels = tf.unstack(labels, num = params['batch_size']) # list of [1] inputs = tf.unstack(input_embedding_vector, num = params['batch_size']) # list of [emb_size] for label, input in zip(labels, inputs): path = self.path_table[tf.squeeze(label)]# (max_depth,) code = self.code_table[tf.squeeze(label)] # (max_depth,) path = tf.boolean_mask(path, tf.not_equal(path, INVALID_INDEX)) # (real_path_length,) code = tf.boolean_mask(code, tf.not_equal(code, INVALID_INDEX) ) # (real_path_length,) output_embedding_vector = tf.nn.embedding_lookup(output_embedding, path) # real_path_length * emb_size bias = tf.nn.embedding_lookup(output_bias, path) # (real_path_length,) logits = tf.matmul(tf.expand_dims(input, axis=0), tf.transpose(output_embedding_vector) ) + bias # (1,emb_size) *(emb_size, real_path_length) loss.append(tf.nn.sigmoid_cross_entropy_with_logits(labels = code, logits = tf.squeeze(logits) )) loss = tf.reduce_mean(tf.concat(loss, axis = 0), axis=0, name = 'hierarchy_softmax_loss') # batch -> scaler return loss ``` ### Negative Sampling Negative Sampling理解起來更加直觀，因為模型的目標是訓練出高質量的word embedding，也就是input word embedding，那是否每個batch都更新全部的output word embedding並不重要，我們可以每次只sample K個embedding來做更新。原始的正樣本保留，我們再取樣 K組負樣本來進行訓練，模型只需要學習正樣本vs負樣本，也就繞過了用V個單詞來做歸一化的問題，把多分類問題成功簡化為二分類問題。作者表示小樣本K=5~20，大樣本k=2~5。 對應上述的模型推導，hidden->output的部分發生變化, 損失函式變為 $$ E = -log\sigma(v_j^Th) - \sum_{w_j \in neg} log\sigma(-v_{w_j}^Th) $$ 每個iteration只有K個embedding被更新 $$ v_{w^{'}j}^{(new)} = v_{w^{'}j}^{(old)} - \eta \cdot e_j \cdot h \,\,\,\, \text{where } j \in k $$ 而input->hidden的部分,只有k個embedding的加權向量會用於輸入embedding的更新 $$ v_{w_I}^{(new)} = v_{w_I}^{(old)} - \eta \cdot \sum_{j=1}^K e_j \cdot v_{w^{'}j} $$ tensorflow有幾種candidate sample的實現，兩種比較常用的是nn.sampled_softmax_loss和nn.nce_loss, 它們呼叫了相同的取樣函式。差異在於sampled_softmax_loss用的是softmax（排他單分類)，而nce_loss是求logistic (不排他多分類）。這兩種實現都和negative sampling有些許差異，細節可以看下[Notes on Noise Contrastive Estimation and Negative Sampling][3]。而這二者之間比較是有觀點說nce更適合skip-gram, sample更適合CBOW，具體差異我也還得再多用用試試看。 ### Subsampling 論文還有一個重點是subsampling，針對出現頻率高的詞，對於它們過多的訓練樣本不能進一步提高表現，因此可以對這些樣本進行downsample。t是詞頻閾值， $f(w_i)$是單詞在corpus裡的出現頻率，所有出現頻率高於t的單詞，都會按照以下概率被降取樣 $$ p(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}} $$ ## 模型實現 手殘黨現實體驗是word2vec比較複雜的部分不是模型。。。而是input_pipe和loss function，所以在實現的時候也希望儘可能把dataset, model_fn, 和train的部分分割開來。以下只給出model_fn的核心部分 ```python def avg_pooling_embedding(embedding, features, params): """ :param features: (batch, 2*window_size) :param embedding: (vocab_size, emb_size) :return: input_embedding : average pooling of context embedding """ input_embedding= [] samples = tf.unstack(features, params['batch_size']) for sample in samples: sample = tf.boolean_mask(sample, tf.not_equal(sample, INVALID_INDEX), axis=0) # (real_size,) tmp = tf.nn.embedding_lookup(embedding, sample) # (real_size, emb_size) input_embedding.append(tf.reduce_mean(tmp, axis=0)) # (emb_size, ) input_embedding = tf.stack(input_embedding, name = 'input_embedding_vector') # batch * emb_size return input_embedding def model_fn(features, labels, mode, params): if params['train_algo'] == 'HS': # If Hierarchy Softmax is used, initialize a huffman tree first hstree = HierarchySoftmax( params['freq_dict'] ) hstree.build_tree() hstree.traverse() hstree.convert2tensor() if params['model'] == 'CBOW': features = tf.reshape(features, shape = [-1, 2 * params['window_size']]) labels = tf.reshape(labels, shape = [-1,1]) else: features = tf.reshape(features, shape = [-1,]) labels = tf.reshape(labels, shape = [-1,1]) with tf.variable_scope( 'initialization' ): w0 = tf.get_variable( shape=[params['vocab_size'], params['emb_size']], initializer=tf.truncated_normal_initializer(), name='input_word_embedding' ) if params['train_algo'] == 'HS': w1 = tf.get_variable( shape=[hstree.num_node, params['emb_size']], initializer=tf.truncated_normal_initializer(), name='hierarchy_node_embedding' ) b1 = tf.get_variable( shape = [hstree.num_node], initializer=tf.random_uniform_initializer(), name = 'bias') else: w1 = tf.get_variable( shape=[params['vocab_size'], params['emb_size']], initializer=tf.truncated_normal_initializer(), name='output_word_embedding' ) b1 = tf.get_variable( shape=[params['vocab_size']], initializer=tf.random_uniform_initializer(), name='bias') add_layer_summary( w0.name, w0) add_layer_summary( w1.name, w1 ) add_layer_summary( b1.name, b1 ) with tf.variable_scope('input_hidden'): # batch_size * emb_size if params['model'] == 'CBOW': input_embedding_vector = avg_pooling_embedding(w0, features, params) else: input_embedding_vector = tf.nn.embedding_lookup(w0, features, name = 'input_embedding_vector') add_layer_summary(input_embedding_vector.name, input_embedding_vector) with tf.variable_scope('hidden_output'): if params['train_algo'] == 'HS': loss = hstree.get_loss( input_embedding_vector, labels, w1, b1, params) else: loss = negative_sampling(mode = mode, output_embedding = w1, bias = b1, labels = labels, input_embedding_vector =input_embedding_vector, params = params) optimizer = tf.train.AdagradOptimizer( learning_rate = params['learning_rate'] ) update_ops = tf.get_collection( tf.GraphKeys.UPDATE_OPS ) with tf.control_dependencies( update_ops ): train_op = optimizer.minimize( loss, global_step= tf.train.get_global_step() ) return tf.estimator.EstimatorSpec( mode, loss=loss, train_op=train_op ) ``` 留言，評論，吐槽程式碼的都歡迎哈～ ---- ## Ref 1. [Word2Vec A]Tomas Mikolov et al, 2013, Efficient Edtimation of Word Representations in Vector Space 2. [Word2Vec B]Tomas Mikolow et al, 2013, Distributed Representations of Words and Phrases and their Compositionality 3. Yoav GoldBerg, Omer Levy, 2014, Wor2Vec Explained: Deribing Mikolow et al's Negative-Sampling Word Embedding Method 4. Xin Rong, 2016, word2vec ParameterLearning Explained 5. [Candidate Sampling]https://www.tensorflow.org/extras/candidate_sampling.pdf 6. [Negative Sampling]Chris Dyer, 2014, Notes on Noise Contrastive Estimation and Negative Sampling 7. https://github.com/chao-ji/tf-word2vec 8. https://github.com/akb89/word2vec 9. https://ruder.io/word-embeddings-softmax/index.html#negativesampling 10. https://blog.csdn.net/lilong117194/article/details/82849054 [1]: https://medium.com/iecse-hashtag/huffman-coding-compression-basics-in-python-6653cdb4c476 [2]: https://www.quora.com/What-is-hierarchical-softmax [3]: http://demo.clab.cs.cmu.edu/cdyer/nce_n