KMP演算法詳解 以及程式碼實現
KMP演算法求解什麼型別問題
字串匹配。給你兩個字串,尋找其中一個字串是否包含另一個字串,如果包含,返回包含的起始位置。
如下面兩個字串:
char *str = "bacbababadababacambabacaddababacasdsd";
char *ptr = "ababaca";str有兩處包含ptr
分別在str的下標10,26處包含ptr。
“bacbababadababacambabacaddababacasdsd”;\
問題型別很簡單,下面直接介紹演算法
演算法說明
一般匹配字串時,我們從目標字串str(假設長度為n)的第一個下標選取和ptr長度(長度為m)一樣的子字串進行比較,如果一樣,就返回開始處的下標值,不一樣,選取str下一個下標,同樣選取長度為n的字串進行比較,直到str的末尾(實際比較時,下標移動到n-m)。這樣的時間複雜度是O(n*m)
KMP演算法:可以實現複雜度為O(m+n)
為何簡化了時間複雜度:
充分利用了目標字串ptr的性質(比如裡面部分字串的重複性,即使不存在重複欄位,在比較時,實現最大的移動量)。
上面理不理解無所謂,我說的其實也沒有深刻剖析裡面的內部原因。
考察目標字串ptr:
ababaca
這裡我們要計算一個長度為m的轉移函式next。
next陣列的含義就是一個固定字串的最長字首和最長字尾相同的長度。
比如:abcjkdabc,那麼這個陣列的最長字首和最長字尾相同必然是abc。
cbcbc,最長字首和最長字尾相同是cbc。
abcbc,最長字首和最長字尾相同是不存在的。
**注意最長字首:是說以第一個字元開始,但是不包含最後一個字元。
比如aaaa相同的最長字首和最長字尾是aaa。**
對於目標字串ptr,ababaca
a,ab,aba,abab,ababa,ababac,ababaca的相同的最長字首和最長字尾的長度。由於a,ab,aba,abab,ababa,ababac,ababaca的相同的最長字首和最長字尾是“”,“”,“a”,“ab”,“aba”,“”,“a”,所以next陣列的值是[-1,-1,0,1,2,-1,0],這裡-1表示不存在,0表示存在長度為1,2表示存在長度為3。這是為了和程式碼相對應。
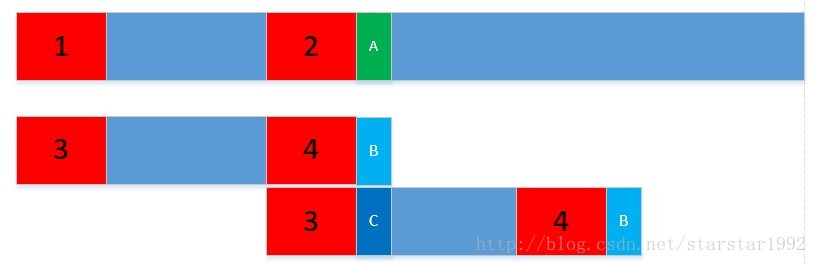
下圖中的1,2,3,4是一樣的。1-2之間的和3-4之間的也是一樣的,我們發現A和B不一樣;之前的演算法是我把下面的字串往前移動一個距離,重新從頭開始比較,那必然存在很多重複的比較。現在的做法是,我把下面的字串往前移動,使3和2對其,直接比較C和A是否一樣。
程式碼解析
void cal_next(char *str, int *next, int len)
{
next[0] = -1;//next[0]初始化為-1,-1表示不存在相同的最大字首和最大字尾
int k = -1;//k初始化為-1
for (int q = 1; q <= len-1; q++)
{
while (k > -1 && str[k + 1] != str[q])//如果下一個不同,那麼k就變成next[k],注意next[k]是小於k的,無論k取任何值。
{
k = next[k];//往前回溯
}
if (str[k + 1] == str[q])//如果相同,k++
{
k = k + 1;
}
next[q] = k;//這個是把算的k的值(就是相同的最大字首和最大字尾長)賦給next[q]
}
}KMP
這個和next很像,具體就看程式碼,其實上面已經大概說完了整個匹配過程。
int KMP(char *str, int slen, char *ptr, int plen)
{
int *next = new int[plen];
cal_next(ptr, next, plen);//計算next陣列
int k = -1;
for (int i = 0; i < slen; i++)
{
while (k >-1&& ptr[k + 1] != str[i])//ptr和str不匹配,且k>-1(表示ptr和str有部分匹配)
k = next[k];//往前回溯
if (ptr[k + 1] == str[i])
k = k + 1;
if (k == plen-1)//說明k移動到ptr的最末端
{
//cout << "在位置" << i-plen+1<< endl;
//k = -1;//重新初始化,尋找下一個
//i = i - plen + 1;//i定位到該位置,外層for迴圈i++可以繼續找下一個(這裡預設存在兩個匹配字串可以部分重疊),感謝評論中同學指出錯誤。
return i-plen+1;//返回相應的位置
}
}
return -1;
}測試
char *str = "bacbababadababacambabacaddababacasdsd";
char *ptr = "ababaca";
int a = KMP(str, 36, ptr, 7);
return 0;注意如果str裡有多個匹配ptr的字串,要想求出所有的滿足要求的下標位置,在KMP演算法需要稍微修改一下。見上面註釋掉的程式碼。
複雜度分析
next函式計算複雜度是(m),開始以為是O(m^2),後來仔細想了想,cal__next裡的while迴圈,以及外層for迴圈,利用均攤思想,其實是O(m),這個以後想好了再寫上。
………………………………………..分割線……………………………………..
其實本文已經結束,後面的只是針對評論裡的疑問,我嘗試著進行解答的。
進一步說明(2018-3-14)
看了評論,大家對cal_next(..)函式和KMP()函式裡的
while (k > -1 && str[k + 1] != str[q])
{
k = next[k];
}和
while (k >-1&& ptr[k + 1] != str[i])
k = next[k];這個while迴圈和k=next[k]很疑惑!
確實啊,我開始看這幾行程式碼,相當懵逼,這寫的啥啊,為啥這樣寫;後來上機跑了一下,慢慢了解到為何這樣寫了。這幾行程式碼,可謂是對KMP演算法本質得了解非常清楚才能想到的。很牛逼!
直接看cal_next(..)函式:
首先我們看第一個while迴圈,它到底幹了什麼。
在此之前,我們先回到原程式。原程式裡有一個大的for()迴圈,那這個for()迴圈是幹嘛的?
這個for迴圈就是計算next[0],next[1],…next[q]…的值。
裡面最後一句next[q]=k就是說明每次迴圈結束,我們已經計算了ptr的前(q+1)個字母組成的子串的“相同的最長字首和最長字尾的長度”。(這句話前面已經解釋了!) 這個“長度”就是k。
好,到此為止,假設迴圈進行到 第 q 次,即已經計算了next[q],我們是怎麼計算next[q+1]呢?
比如我們已經知道ababab,q=4時,next[4]=2(k=2,表示該字串的前5個字母組成的子串ababa存在相同的最長字首和最長字尾的長度是3,所以k=2,next[4]=2。這個結果可以理解成我們自己觀察算的,也可以理解成程式自己算的,這不是重點,重點是程式根據目前的結果怎麼算next[5]的).,那麼對於字串ababab,我們計算next[5]的時候,此時q=5, k=2(上一步迴圈結束後的結果)。那麼我們需要比較的是str[k+1]和str[q]是否相等,其實就是str[1]和str[5]是否相等!,為啥從k+1比較呢,因為上一次迴圈中,我們已經保證了str[k]和str[q](注意這個q是上次迴圈的q)是相等的(這句話自己想想,很容易理解),所以到本次迴圈,我們直接比較str[k+1]和str[q]是否相等(這個q是本次迴圈的q)。
如果相等,那麼跳出while(),進入if(),k=k+1,接著next[q]=k。即對於ababab,我們會得出next[5]=3。 這是程式自己算的,和我們觀察的是一樣的。
如果不等,我們可以用”ababac“描述這種情況。 不等,進入while()裡面,進行k=next[k],這句話是說,在str[k + 1] != str[q]的情況下,我們往前找一個k,使str[k + 1]==str[q],是往前一個一個找呢,還是有更快的找法呢? (特別注意:一個一個找不可以,即你把 k = next[k] 換成k- -是不行的(把k=next[k]換成k–是不行的,while (k > -1 && str[k + 1] != str[q]) { //k--;//也能執行}。 k--貌似不行吧,後面是說明,不對請指出哈。 k = next[k] 這一句其實包含了條件,str[k] = str[q - 1]且長度為k的字首應該和str[q - 1]結尾的字尾相同,k--則有可能提前跳出迴圈,導致長度為k的字首應該和str[q - 1]結尾的字尾相同不滿足。比如串“acceaccc”, 但q為最後一個c時,next[7]應該等於-1。但如果用k--來做的話,迴圈到q等於7時,next[6] = 2,k = 2,滿足while迴圈條件,進入迴圈,當k=1時,跳出迴圈,str[k + 1] = str[7],得到next[7] = 2,正確的應該next[7] = -1。而且換成k=next[q-1]也不行,如:abababa,會出現死迴圈。)。但是程式給出了一種更快的找法,那就是 k = next[k]。 程式的意思是說,一旦str[k + 1] != str[q],即在後綴裡面找不到時,我是可以直接跳過中間一段,跑到字首裡面找,next[k]就是相同的最長字首和最長字尾的長度。所以,k=next[k]就變成,k=next[2],即k=0。此時再比較str[0+1]和str[5]是否相等,不等,則k=next[0]=-1。跳出迴圈。
(這個解釋能懂不?)
以上就是這個cal_next()函式裡的
while (k > -1 && str[k + 1] != str[q])
{
k = next[k];
}最難理解的地方的一個我的理解,有不對的歡迎指出。
複雜度分析:
分析KMP複雜度,那就直接看KMP函式。
int KMP(char *str, int slen, char *ptr, int plen)
{
int *next = new int[plen];
cal_next(ptr, next, plen);//計算next陣列
int k = -1;
for (int i = 0; i < slen; i++)
{
while (k >-1&& ptr[k + 1] != str[i])//ptr和str不匹配,且k>-1(表示ptr和str有部分匹配)
k = next[k];//往前回溯
if (ptr[k + 1] == str[i])
k = k + 1;
if (k == plen-1)//說明k移動到ptr的最末端
{
//cout << "在位置" << i-plen+1<< endl;
//k = -1;//重新初始化,尋找下一個
//i = i - plen + 1;//i定位到該位置,外層for迴圈i++可以繼續找下一個(這裡預設存在兩個匹配字串可以部分重疊),感謝評論中同學指出錯誤。
return i-plen+1;//返回相應的位置
}
}
return -1;
}這玩意真的不好解釋,簡單說一下:
從程式碼解釋複雜度是一件比較難的事情,我們從
這個圖來解釋。
我們可以看到,匹配串每次往前移動,都是一大段一大段移動,假設匹配串裡不存在重複的字首和字尾,即next的值都是-1,那麼每次移動其實就是一整個匹配串往前移動m個距離。然後重新一一比較,這樣就比較m次,概括為,移動m距離,比較m次,移到末尾,就是比較n次,O(n)複雜度。 假設匹配串裡存在重複的字首和字尾,我們移動的距離相對小了點,但是比較的次數也小了,整體代價也是O(n)。
所以複雜度是一個線性的複雜度。
整體程式碼:
#include<iostream>
#include<cstdio>
#include<string.h>
using namespace std;
void solve_next(char *a,int *next,int len)
{
int k=-1;
next[0]=-1;
for(int i=1;i<len;i++)
{
while(k>-1&&a[k+1]!=a[i])
k=next[k];
if(a[k+1]==a[i])
k++;
next[i]=k;
}
}
void KMP(char *str,int slen,char *ptr,int plen)
{
int *next=new int[plen];
solve_next(ptr,next,plen);
int k=-1;
for(int i=0;i<slen;i++)
{
while(k>-1&&ptr[k+1]!=str[i])
k=next[k];
if(ptr[k+1]==str[i])
k++;
if(k==plen-1)
{
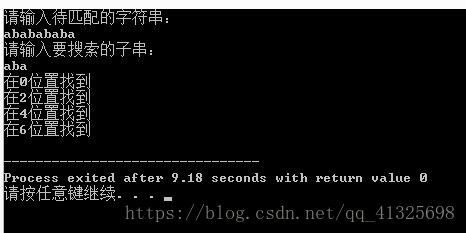
cout<<"在"<<i-plen+1<<"位置找到"<<endl;
i=i-plen+1;
k=-1;
}
}
}
int main()
{
char str[100],ptr[10];
cout<<"請輸入待匹配的字串:"<<endl;
scanf("%s",str);
cout<<"請輸入要搜尋的子串:"<<endl;
scanf("%s",ptr);
KMP(str,strlen(str),ptr,strlen(ptr));
return 0;
}