七夕也要學起來,雜湊雜湊雜湊!
阿新 • • 發佈:2020-08-25

# 前言
> 本文收錄於專輯:[http://dwz.win/HjK](http://dwz.win/HjK),點選解鎖更多資料結構與演算法的知識。
你好,我是彤哥。
上一節,我們一起學習了,在Java中如何構建高效能佇列,裡面牽涉到很多底層的知識,不知道你有Get到多少呢?!
本節,我想跟著大家一起重新學習下關於雜湊的一切——雜湊、雜湊函式、雜湊表。
這三者有什麼樣的愛恨情仇?
為什麼Object類中需要有一個hashCode()方法?它跟equals()方法有什麼關係?
如何編寫一個高效能的雜湊表?
Java中的HashMap中的紅黑樹可以使用其它資料結構替換嗎?
# 何為雜湊?
Hash,是指把任意長度的輸入通過一定的演算法變成**固定長度的輸出**的過程,這個輸出稱作Hash值,或者Hash碼,這個演算法叫做Hash演算法,或者Hash函式,這個過程我們一般就稱作Hash,或者計算Hash,Hash翻譯為中文有雜湊、雜湊、雜湊等。
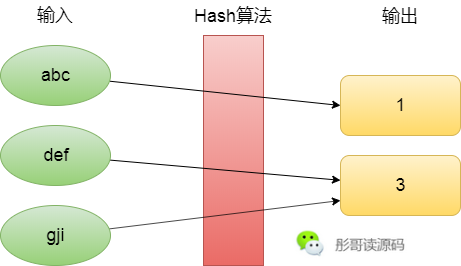
既然是固定長度的輸出,那就意味著輸入是無限多的,輸出是有限的,必然會出現不同的輸入可能會得到相同的輸出的情況,所以,Hash演算法一般來說也是不可逆的。
那麼,Hash演算法有哪些用途呢?
# 雜湊演算法的用途
雜湊演算法,是一種廣義的演算法,或者說是一種思想,它沒有一個固定的公式,只要滿足上面定義的演算法,都可以稱作Hash演算法。
通常來說,它具有以下用途:
1. 加密密碼,比如,使用MD5+鹽的方式來加密密碼;
2. 快速查詢,比如,雜湊表的使用,通過雜湊表能夠快速查詢元素;
3. 數字簽名,比如,系統間呼叫加上簽名,可以防止篡改資料;
4. 檔案檢驗,比如,下載騰訊遊戲的時候通常都有有一個MD5值,安裝包下載下來之後計算出來一個MD5值與官方的MD5值進行對比,就可知道下載過程中有沒有檔案損壞,有沒有被篡改等;
好了,說起Hash演算法,或者Hash函式,在Java中,所有物件的父類Object都有一個Hash函式,即hashCode()方法,為什麼Object類中需要定義這麼一個方法呢?
> 嚴格來說,Hash演算法和Hash函式還是有點區別的,相信你能根據語境進行區分。
讓我們來看看JDK原始碼的註釋怎麼說:

請看紅框的部分,翻譯一下大致為:為這個物件返回一個Hash值,它是為了更好地支援雜湊表而存在的,比如HashMap。簡單點說,這個方法就是給HashMap等雜湊表使用的。
```java
// 預設返回的是物件的內部地址
public native int hashCode();
```
此時,我們不得不提起Object類中的另一個方法——equals()。
```java
// 預設是直接比較兩個物件的地址是否相等
public boolean equals(Object obj) {
return (this == obj);
}
```
hashCode()和equals又有怎樣的糾纏呢?
通常來說,hashCode()可以看作是一種弱比較,迴歸Hash的本質,將不同的輸入對映到固定長度的輸出,那麼,就會出現以下幾種情況:
1. 輸入相同,輸出必然相同;
2. 輸入不同,輸出可能相同,也可能不同;
3. 輸出相同,輸入可能相同,也可能不同;
4. 輸出不同,輸入必然不同;
而equals()是嚴格比較兩個物件是否相等的方法,所以,如果兩個物件equals()為true,那麼,它們的hashCode()一定要相等,如果不相等會怎樣呢?
如果equals()返回true,而hashCode()不相等,那麼,試想將這兩個物件作為HashMap的key,它們很大可能會定位到HashMap不同的槽中,此時就會出現一個HashMap中插入了兩個相等的物件,這是不允許的,這也是為什麼重寫了equals()方法一定要重寫hashCode()方法的原因。
比如,String這個類,我們都知道它的equals()方法是比較兩個字串的內容是否相等,而不是兩個字串的地址,下面是它的equals()方法:
```java
public boolean equals(Object anObject) {
if (this == anObject) {
return true;
}
if (anObject instanceof String) {
String anotherString = (String)anObject;
int n = value.length;
if (n == anotherString.value.length) {
char v1[] = value;
char v2[] = anotherString.value;
int i = 0;
while (n-- != 0) {
if (v1[i] != v2[i])
return false;
i++;
}
return true;
}
}
return false;
}
```
所以,對於下面這兩個字串物件,使用equals()比較它們是相等的,而它們的記憶體地址並不相同:
```java
String a = new String("123");
String b = new String("123");
System.out.println(a.equals(b)); // true
System.out.println(a == b); // false
```
此時,如果不重寫hashCode()方法,那麼,a和b將返回不同的hash碼,對於我們常常使用String作為HashMap的key將造成巨大的干擾,所以,String重寫的hashCode()方法:
```java
public int hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i < value.length; i++) {
h = 31 * h + val[i];
}
hash = h;
}
return h;
}
```
這個演算法也很簡單,用公式來表示為:s[0]\*31^(n-1) + s[1]\*31^(n-2) + ... + s[n-1]。
好了,既然這裡屢次提到雜湊表,那我們就來看看雜湊表是如何一步步進化的。
# 雜湊表進化史
## 陣列
講雜湊表之前,我們先來看看資料結構的鼻祖——陣列。
陣列比較簡單,我就不多說了,大家都會都懂,見下圖。

陣列的下標一般從0開始,依次往後儲存元素,查詢指定元素也是一樣,只能從頭(或從尾)依次查詢元素。
比如,要查詢4這個元素,從頭開始查詢的話需要查詢3次。
## 早期的雜湊表
上面講了陣列的缺點,查詢某個元素只能從頭或者從尾依次查詢元素,直到匹配為止,它的均衡時間複雜是O(n)。
那麼,利用陣列有沒有什麼方法可以快速的查詢元素呢?
聰明的程式設計師哥哥們想到一種方法,通過雜湊函式計算元素的值,用這個值確定元素在陣列中的位置,這樣時間複雜度就能縮短到O(1)了。
比如,有5個元素分別為3、5、4、1,把它們放入到陣列之前先通過雜湊函式計算位置,精確放置,而不是像簡單陣列那樣依次放置元素(基於索引而不是元素值來查詢位置)。
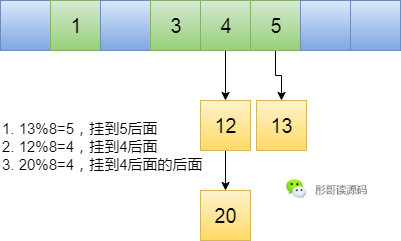
假如,這裡申請的陣列長度為8,我們可以造這麼一個雜湊函式為hash(x) = x % 8,那麼最後的元素就變成了下圖這樣:

這時候我們再查詢4這個元素,先算一下它的hash值為hash(4) = 4 % 8 = 4,所以直接返回4號位置的元素就可以了。
## 進化的雜湊表
事情看著挺完美,但是,來了一個元素13,要插入的雜湊表中,算了一下它的hash值為hash(13) = 13 % 8 = 5,納尼,它計算的位置也是5,可是5號已經被人先一步佔領了,怎麼辦呢?
這就是**雜湊衝突**。
### 為什麼會出現雜湊衝突呢?
因為我們申請的陣列是有限長度的,把無限的數字對映到有限的陣列上早晚會出現衝突,即多個元素對映到同一個位置上。
好吧,既然出現了雜湊衝突,那麼我們就要解決它,必須幹!
How to?
### 線性探測法
既然5號位置已經有主了,那我元素13認慫,我往後挪一位,我到6號位置去,這就是線性探測法,當出現衝突的時候依次往後挪直到找到空位置為止。

然鵝,又來了個新元素12,算得其hash值為hash(12) = 12 % 8 = 4,What?按照這種方式,要往後移3次到7號位置才有空位置,這就導致了插入元素的效率很低,查詢也是一樣的道理,先定位的4號位置,發現不是我要找的人,再接著往後移,直到找到7號位置為止。
### 二次探測法
使用線性探測法有個很大的弊端,衝突的元素往往會堆積在一起,比如,12號放到7號位置,再來個14號一樣衝突,接著往後再陣列結尾了,再從頭開始放到0號位置,你會發現衝突的元素有聚集現象,這就很不利於查找了,同樣不利於插入新的元素。
這時候又有聰明的程式設計師哥哥提出了新的想法——二次探測法,當出現衝突時,我不是往後一位一位這樣來找空位置,而是使用原來的hash值加上i的二次方來尋找,i依次從1,2,3...這樣,直到找到空位置為止。
還是以上面的為例,插入12號元素,過程是這樣的,本文來源於公主號彤哥讀原始碼:

這樣就能很快地找到空位置放置新元素,而且不會出現衝突元素堆積的現象。
然鵝,又來了新元素20,你瞅瞅放哪?
發現放哪都放不進去了。
研究表明,使用二次探測法的雜湊表,當放置的元素超過一半時,就會出現新元素找不到位置的情況。
所以又引出一個新的概念——擴容。
### 什麼是擴容?
已放置元素達到總容量的x%時,就需要擴容了,這個x%時又叫作**擴容因子**。
很顯然,擴容因子越大越好,表明雜湊表的空間利用率越高。
所以,很遺憾,二次探測法無法滿足我們的目標,擴容因子太小了,只有0.5,一半的空間都是浪費的。
這時候又到了程式設計師哥哥們發揮他們聰明特性的時候了,經過996頭腦風暴後,又想出了一種新的雜湊表實現方式——連結串列法。
## 連結串列法
不就是解決衝突嘛!出現衝突我就不往陣列中去放了,我用一個連結串列把同一個陣列下標位置的元素連線起來,這樣不就可以充分利用空間了嘛,啊哈哈哈哈~~
嘿嘿嘿嘿,完美△△。
真的完美嘛,我是一名黑客,我一直往裡面放\*%8=4的元素,然後你就會發現幾乎所有的元素都跑到同一個連結串列中去了,呵呵,最後的結果就是你的雜湊表退化成了連結串列,查詢插入元素的效率都變成了O(n)。
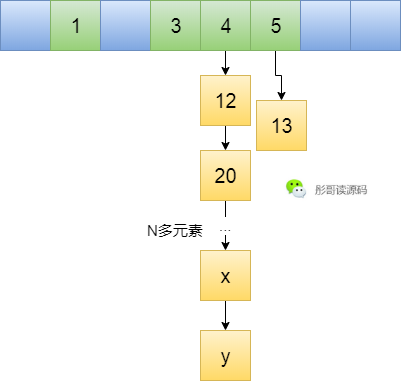
此時,當然有辦法,擴容因子幹啥滴?
比如擴容因子設定為1,當元素個數達到8個時,擴容成兩倍,一半的元素還在4號位置,一半的元素去到了12號位置,能緩解雜湊表的壓力。
然鵝,依舊不是很完美,也只是從一個連結串列變成兩個連結串列,本文來源於公主號彤哥讀原始碼。
聰明的程式設計師哥哥們這次開啟了一次長大9127的頭腦風暴,終於搞出了一種新的結構——連結串列樹法。
## 連結串列樹法
雖然上面的擴容在元素個數比較少的時候能解決一部分問題,整體的查詢插入效率也不會太低,因為元素個數少嘛。
但是,黑客還在攻擊,元素個數還在持續增加,當增加到一定程度的時候,總會導致查詢插入效率特別低。
所以,換個思路,既然連結串列的效率低,我把它升級一下,當連結串列長的時候升級成紅黑樹怎麼樣?
嗯,我看行,說幹就幹。
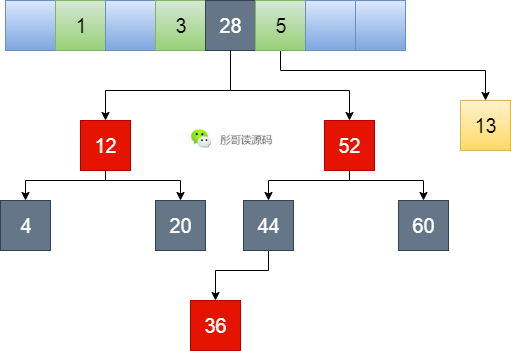
嗯,不錯不錯,媽媽再也不怕我遭到黑客攻擊了,紅黑樹的查詢效率為O(log n),比連結串列的O(n)要高不少。
所以,到這就結束了嗎?
你想多了,每次擴容還是要移動一半的元素好麼,一顆樹分化成兩顆樹,這樣真的好麼好麼好麼?
程式設計師哥哥們太難了,這次經過了12127的頭腦風暴,終於想出個新玩意——一致性Hash。
## 一致性Hash
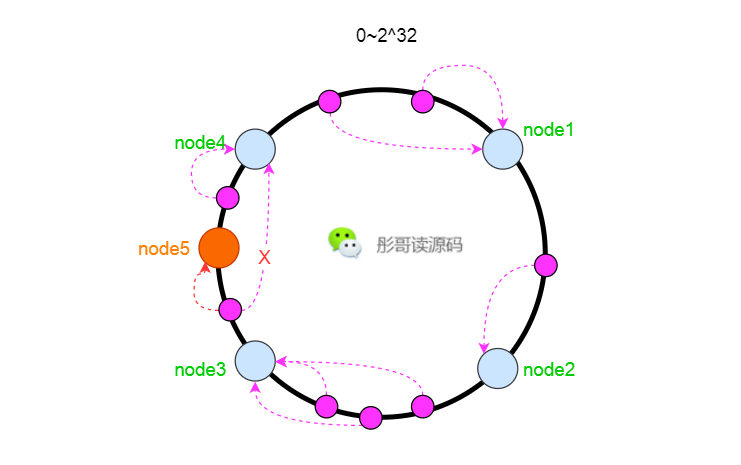
一致性Hash更多地是運用在分散式系統中,比如說Redis叢集部署了四個節點,我們把所有的hash值定義為0~2^32個,每個節點上放置四分之一的元素。
> 此處只為舉例,實際Redis叢集的原理是這樣的,具體數值不是這樣的。
此時,假設需要給Redis增加一個節點,比如node5,放在node3和node4中間,這樣只需要把node3到node4中間的元素從node4移動到node5上面就行了,其它的元素保持不變。
這樣,就增加了擴容的速度,而且影響的元素比較少,大部分請求幾乎無感知。
好了,到這裡關於雜湊表的進化歷史就講到這裡了,你有沒有Get到呢?
# 後記
本節,我們一起重新學習了關於雜湊、雜湊函式、雜湊表相關的知識,在Java中,HashMap的終極形態是以陣列+連結串列+紅黑樹的形式呈現的。
據說,這個紅黑樹還可以換成其它的資料結構,比如跳錶,你造嗎?
下一節,我們就來聊聊**跳錶**這個資料結構,並使用它來改寫HashMap,欲獲取最新推廣,快點來關注我吧!
> 關注公號主“彤哥讀原始碼”,解鎖更多原始碼、基礎、架構
