> 國慶後面兩天划水，甚至想接著發出咕咕咕的叫聲。咳咳咳，這些都不重要!最近學習了一下AC自動機，發現其實遠沒有想象中的那麼難。 ## AC自動機的來歷 我知道，很多人在第一次看到這個東西的時侯是非常興奮的。（別問我為什麼知道） 但AC自動機並不是能自動AC的程式。。。 AC自動機之所以叫AC自動機，是因為這個演算法原名叫 `Aho-Corasick automaton`，是一個叫`Aho-Corasick` 的人發明的。 所以AC自動機也叫做 `Aho-Corasick 演算法` 該演算法在1975年產生於貝爾實驗室，是著名的多模匹配演算法。  ## AC自動機的用處 那麼有的同學可能就有疑問了，AC自動機又不能自動AC，有什麼作用呢？ 其實AC自動機和KMP的用法相似，都是用來解決字串的匹配問題的；但不一樣的是，AC自動機更多的被用來解決多串的匹配問題，換言之，就是有多個子串需要匹配的KMP問題。 例如，例如給幾個單詞 acbs，asf,dsef； 再給出一個 很長的文章（句子），`acbsdfgeasf`； 問在這個文章中，總共出現了多少個單詞，或者是單詞出現的總次數，這就是AC自動機要解決的問題了。  ## AC自動機的實現方法 AC 自動機是 **以 Trie 的結構為基礎** ，結合 **KMP 的思想** 建立的。 簡單來說，建立一個 AC 自動機有兩個步驟： 1. 基礎的 **Trie** 結構：將所有的模式串構成一棵 **Trie**。 2. **KMP** 的思想：對 **Trie** 樹上所有的結點構造失配指標。 然後就可以利用它進行多模式匹配了。 > 不明白**trie**的同學可以 [點選這裡學習](https://www.cnblogs.com/RioTian/p/13780487.html) > > 不瞭解**KMP**的同學可以[點選這裡學習](https://www.cnblogs.com/RioTian/p/12686870.html) 所以就讓我們一起來一步一步實現AC自動機吧！ ### 定義一顆字典樹 首先我們需要定義一顆字典樹，我們用struct來實現各個節點的定義: ```cpp struct node { int next[27]; int fail; int count; void init() { memset(next,-1,sizeof(next)); fail=0; count=0; } }s[1100001]; ``` #### 儲存後驅值的next[]陣列 next[]陣列就是正常Trie樹裡用來儲存每個字元的後一個字元在s數組裡的位置，比如我們讀入一個字串APPLE，那麼： > s【1】儲存的是A，它的next【P】=2，其餘為-1； > s【2】儲存的是P，它的next【P】=3，其餘為-1； > s【3】儲存的是P，它的next【L】=4，其餘為-1； > s【4】儲存的是L，它的next【E】=5，其餘為-1； > s【5】儲存的是E，它的next都為-1。  #### fail：失敗指標 fail為失敗指標，這個在後面的構造會講到如何快速構造，那麼有什麼用呢？ 我們來舉個例子，這個例子這隻顯示了e的失配指標： 我們假設讀入了she，shr，say，her四個單詞，於是我們就得到了一棵可愛的字典樹：  然後我們就只先構造一個失敗指標：  例如匹配文章：sher，我們剛開始從s開始一直向左邊走，走到e後發現：呀，沒有路繼續走了，如果暴力的從h開始又開始一輪匹配就極為浪費時間；這時我們就像，能不能利用之前的匹配資訊呢？可以的！her的字首he剛好和she的he相同，所以我們在she匹配失敗的時候，就跳到了he後面繼續匹配，發現r與r匹配！這就是fail指標的用處，是不是發現和KMP的next陣列非常類似啊！ #### 記錄結尾的count 如果我插入一個單詞APPLE，插入到最後E了，發現這個單詞再也沒有後面的字母了，這時我們就在這個E的count裡面加上一個1，表示有1個單詞以這個e作為結尾。 #### 初始化的init() 我們在這裡還定義了一個初始化函式init()，就是在開創到一個新起點時用來初始化一下的。 ### 在字典樹中插入單詞 我們還是結合程式來講解： ```cpp int ins() { int len=strlen(str+1); int ind=0,i,j; for(int i=1;i<=len;i++) { j=str[i]-'a'+1; if(s[ind].next[j]==-1) { num++; s[num].init(); s[ind].next[j]=num; } ind=s[ind].next[j]; } s[ind].count++; return 0; } ``` 首先str陣列就是我們要讀入的字串，ind表示我現在在s【】陣列中的位置；接下來我們開始迴圈——對於每一個點： > 如果他的前一個字母的next沒有指向他的字母，那麼我們就開創一個新點來儲存這個字母，並且讓他前一個字母的next指向它； > > 如果有直接指向它的字母的位置，那就直接跳過去就好了！ 最後別忘了在每個單詞的末尾的count加上1。 #### 重點！！！快速構造fail指標 #### fail指標有什麼用 首先，fail指標有什麼用？我們繼續使用上一個例子：  我們發現，左邊的e的fail指標指向l最右側的e，那麼這個指標的含義是什麼呢？我們不妨當一個點i指向了一個點j時，我們設從j開始，向上走L個字元就到了最頂點，其中從頂點到j的字串為s； 在這個例子中，s為“he”，長度為L，也就是2；接著從i開始，向上再走L-1個字元，得到一個字串ss，在這個例子中，ss也為“he”！ 這時我們就驚訝的發現，s與ss相同！！ 我們得知，當i的fail指標指向j，頂點到j的字串s是頂點到i的字串的字尾！ 這樣如果i繼續往下匹配失敗的話，就可以不用從頭開始匹配，而是直接從他的fail開始匹配！節省了大量時間！這就是fail指標的精髓所在！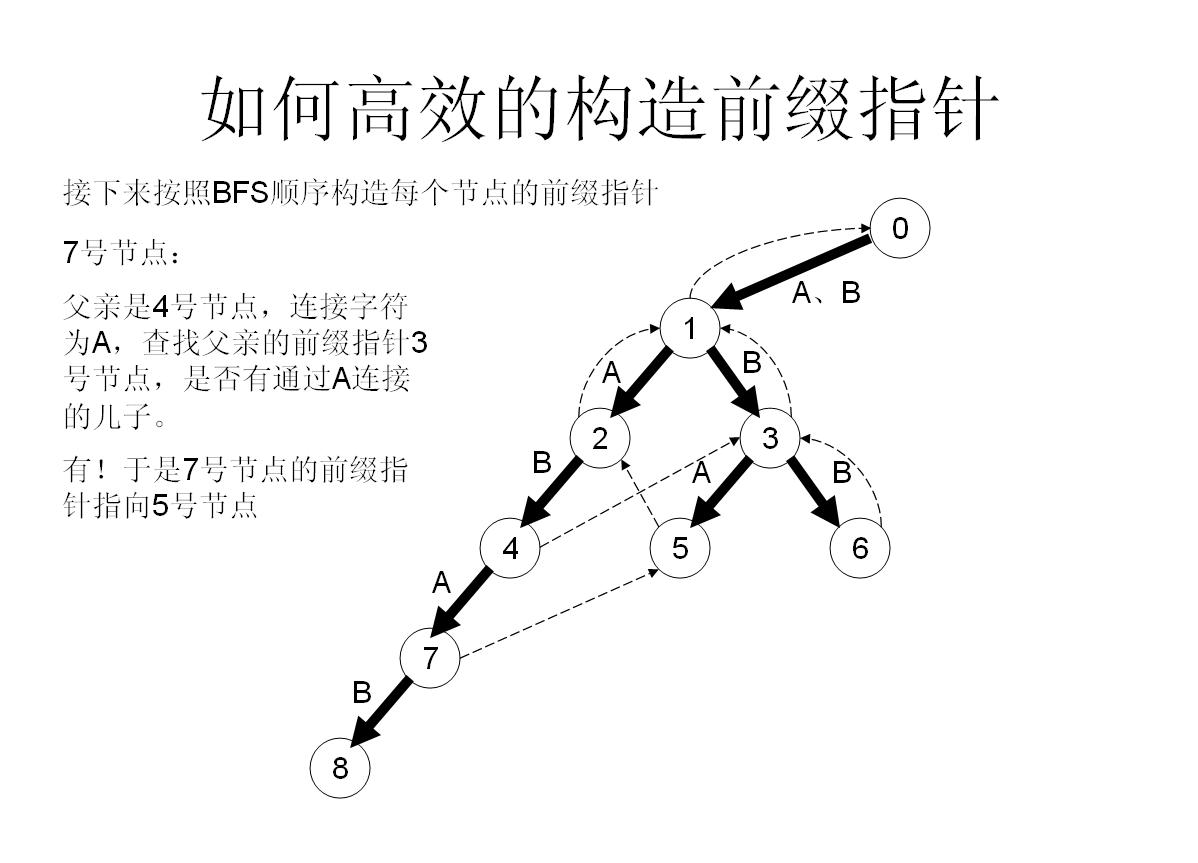 #### fail指標如何構造 我們先貼上程式碼： ```cpp int make_fail() { int head=1,tail=1; int ind,ind_f; for(int i=1;i<=26;i++) { if(s[0].next[i]!=-1) { q[tail]=s[0].next[i]; tail++; } } while(head0 && s[ind_f].next[i]==-1) ind_f=s[ind_f].fail; if(s[ind_f].next[i]!=-1)ind_f=s[ind_f].next[i]; s[s[ind].next[i]].fail=ind_f; } } head++; } return 0; } ``` 首先我們需要開啟一個佇列q，儲存需要處理的點； 接著我們把所有與頂點相連的點加入到佇列裡，然後我們對於佇列裡的每個數進行操作： 首先將他的所有兒子都加到佇列尾部，然後作為一個負責任的父親節點，肯定不能只把兒子們丟到隊尾就完事了，還有做好工作——幫兒子們做好fail指標—— 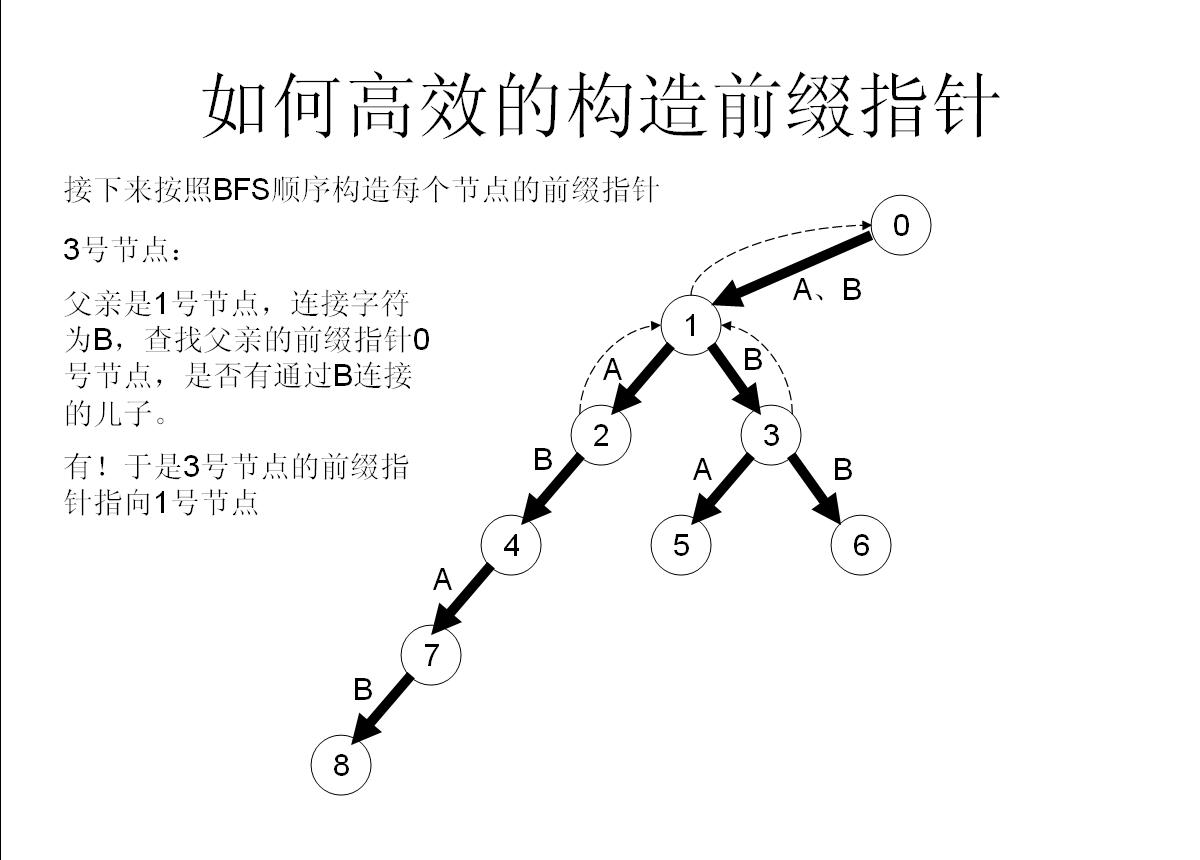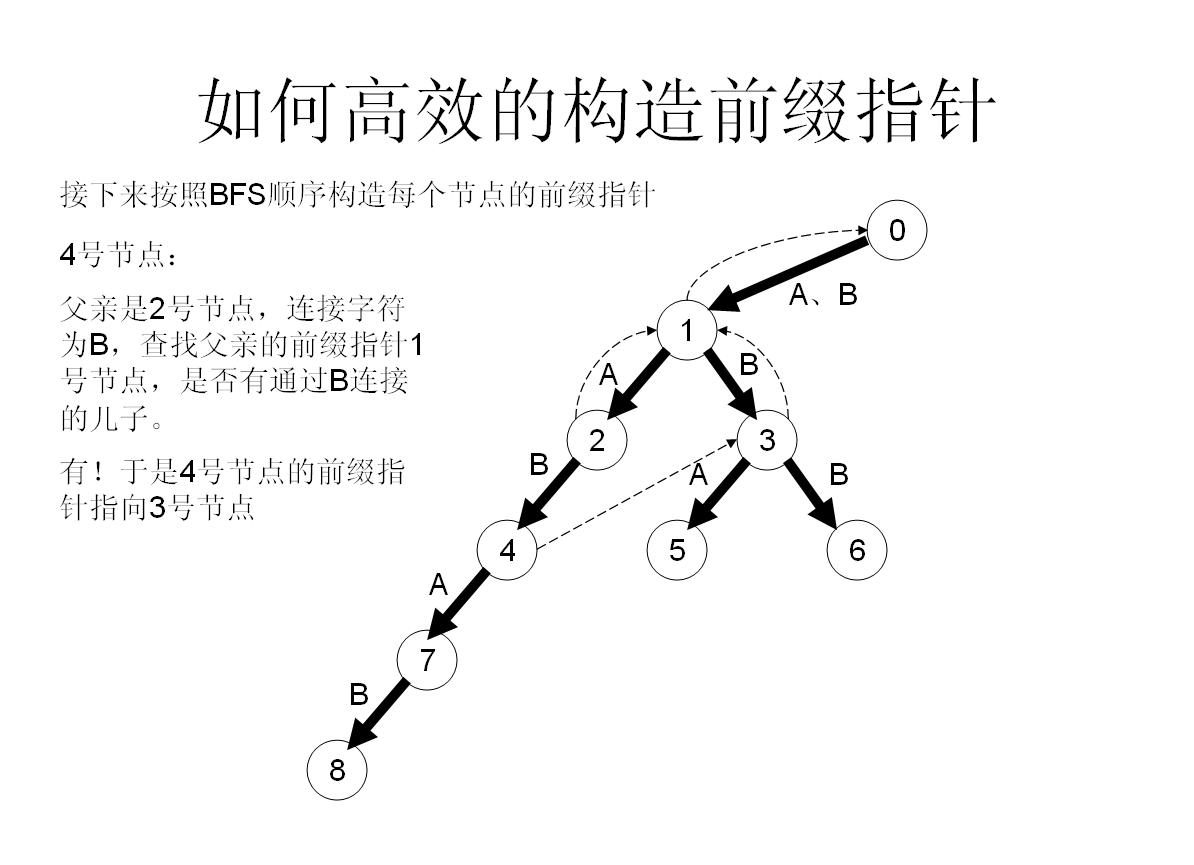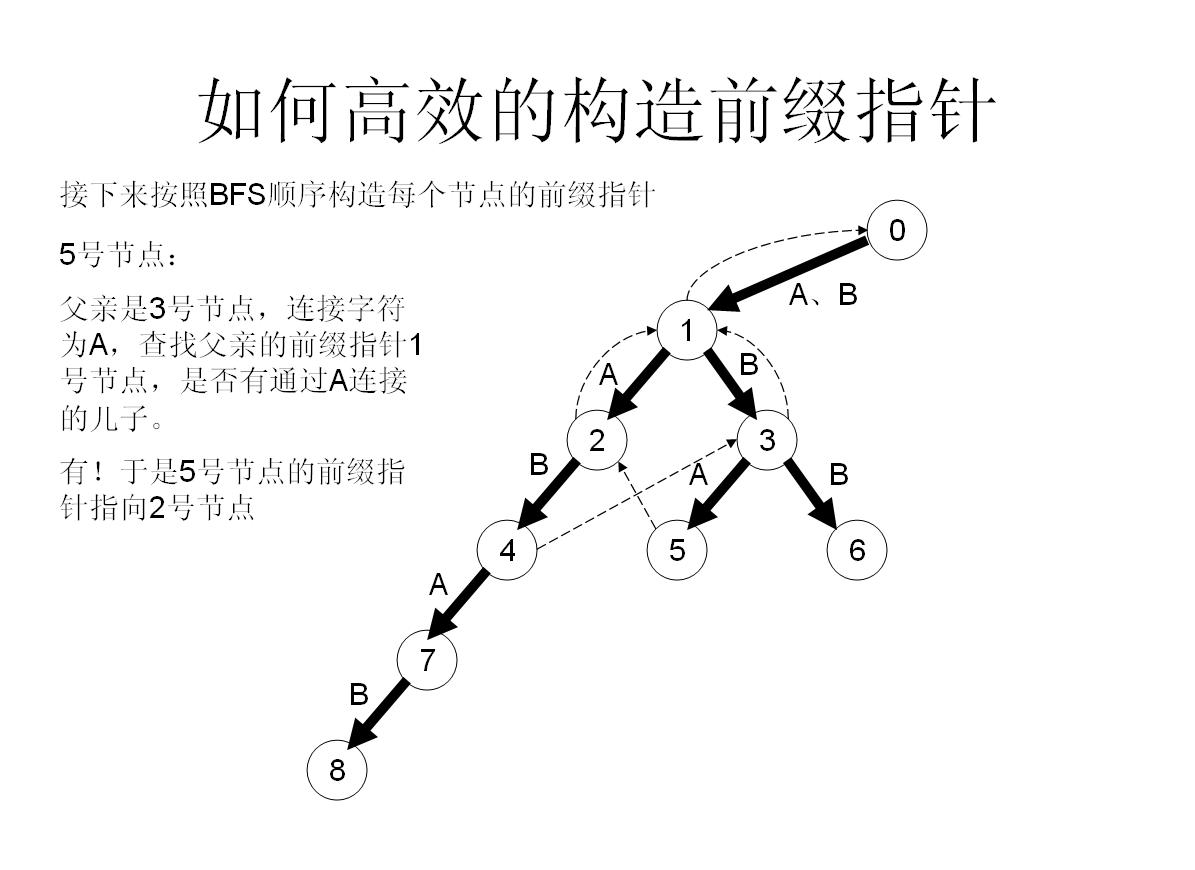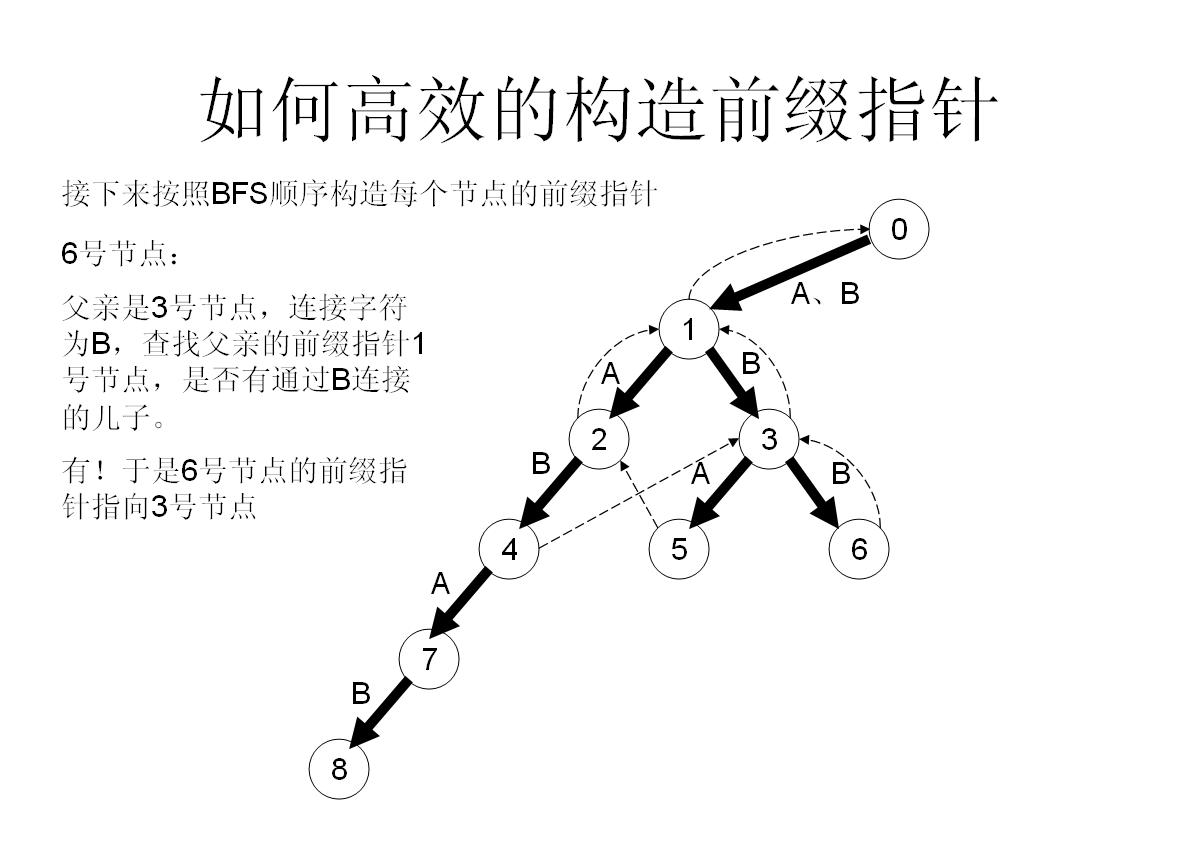首先假如我是那個父親節點x，對於字母a子節點，我先看一下我的fail指標指向的節點y，看一下y有沒有字母a子節點z，如果有，就太好了，我就讓我的子節點的fail指標指向z； 如果沒有，那就從y出發，繼續看他fail指向的點的有沒有字母a的子節點……直到找到滿足條件的點。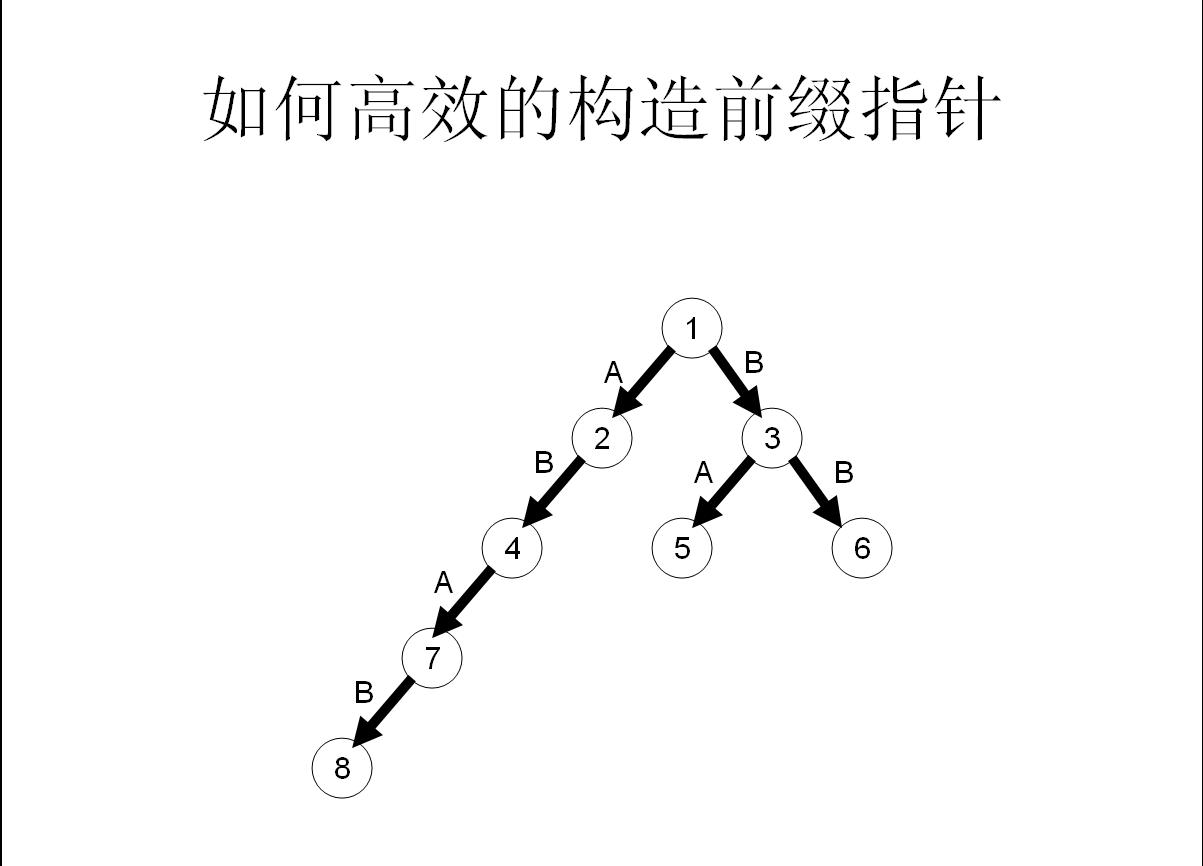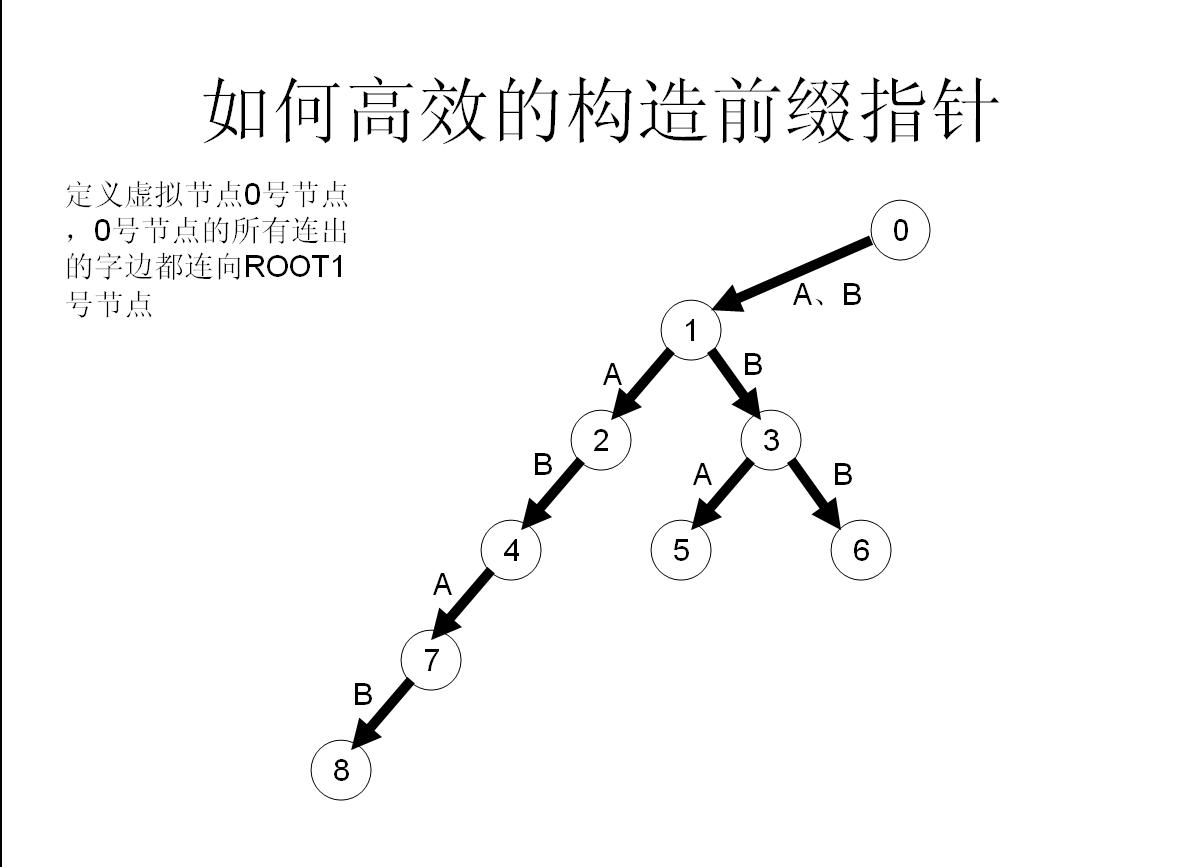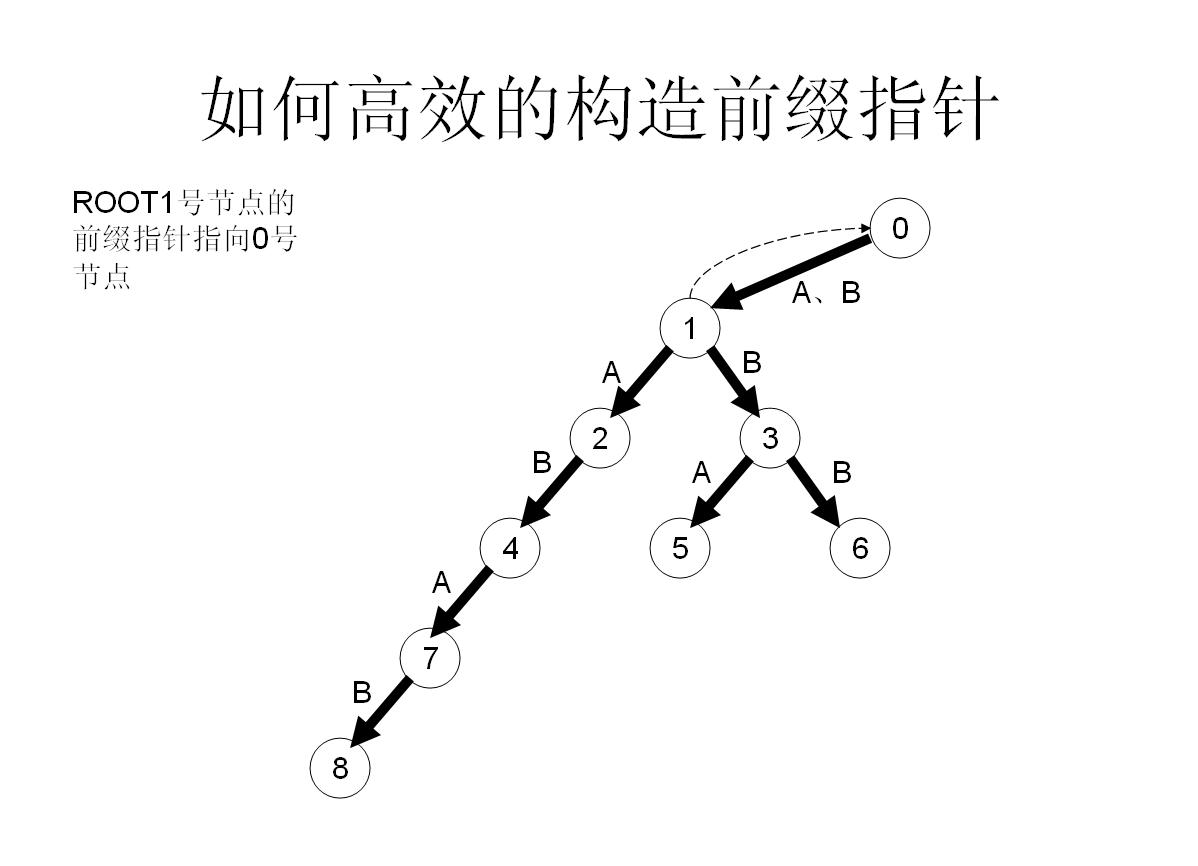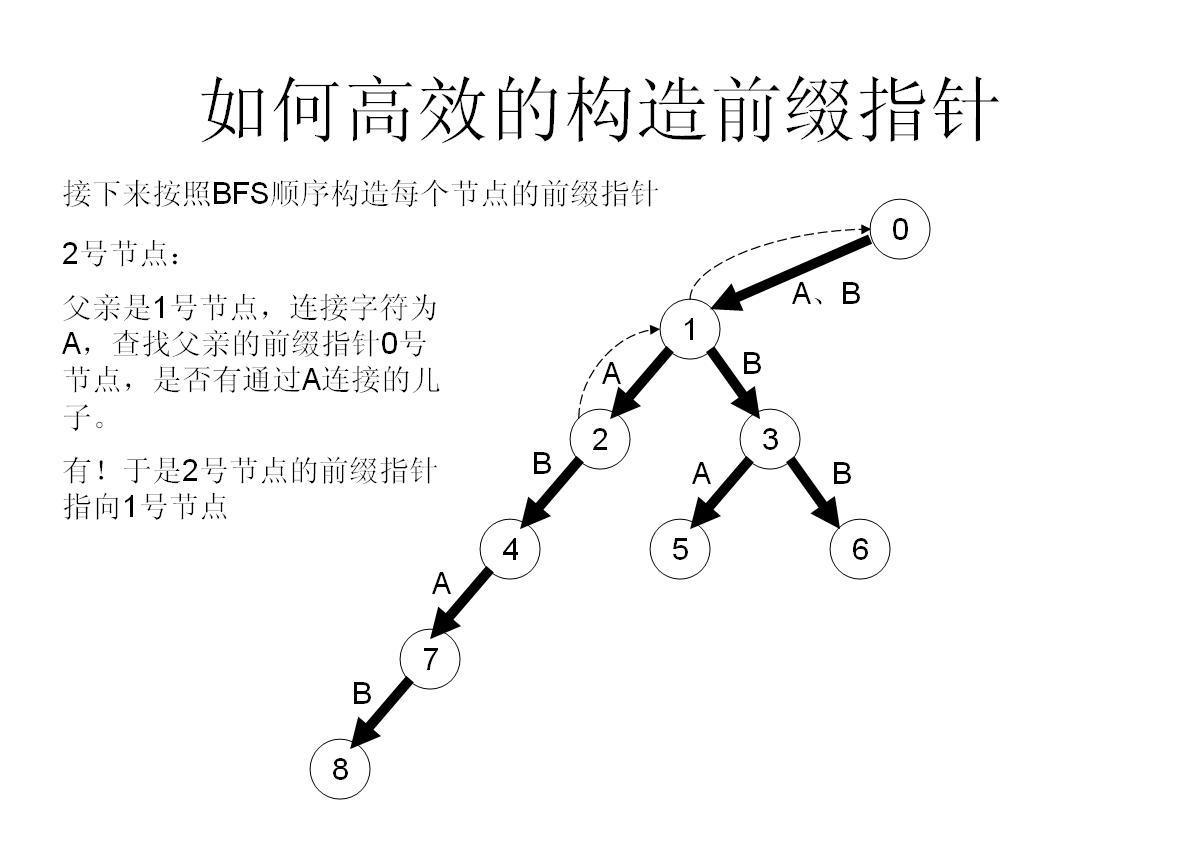 如果實在沒辦法，就算fail一路跳到0號節點也找不到，那就沒辦法了，我的字母a子節點的fail就只好指向0號節點了【因為初始化就為0，所以此時就不用操作了】 我們舉個具體的栗子來看看： [](http://www.jvruo.com/usr/uploads/2018/06/2666801019.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/178621197.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/1746440388.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/3412997009.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/3582182212.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/1499831174.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/1120969507.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/1254946824.jpg) [](http://www.jvruo.com/usr/uploads/2018/06/2725906288.jpg)   所以這樣操作就可以快速構造fail指標了！ #### 進行樹上KMP 我們先看一下程式碼： ```cpp int find() { int len=strlen(des+1); int j,ind=0; for(int i=1;i<=len;i++) { j=des[i]-'a'+1; while(ind>0 && s[ind].next[j]==-1)ind=s[ind].fail; if(s[ind].next[j]!=-1) { ind=s[ind].next[j]; p=ind; while(p>0 && s[p].count!=-1) { ans=ans+s[p].count; s[p].count=-1; p=s[p].fail; } } } return 0; } ``` 一樣的，ind表示我當前匹配好了的點，如果當前點不繼續和IND的任何一個子節點相同，那麼我就跳到ind的fail指標指向的點……知道找到與當前點匹配，或者跳到了根節點，與KMP十分相同！ 需要注意的是由於這道題是求解哪些點在母串中出現，所以我們進行了一層優化： ```cpp while(p>0 && s[p].count!=-1) { ans=ans+s[p].count; s[p].count=-1; p=s[p].fail; } ``` 就是當我們匹配好到一個串s【從根節點到IND的串】的時候，我們就往它的fail一直跳，由於他的fail到根節點的字串ss一定是s的字尾，所以ss在母串中也一定出現，這時就加上它的count再設定為-1，防止後續重複訪問就好了! ## 模板題 > [Luogu p3808] > 題目背景 > 這是一道簡單的AC自動機模板題。 > 用於檢測正確性以及演算法常數。 > 為了防止卡OJ，在保證正確的基礎上只有兩組資料，請不要惡意提交。 > 管理員提示：本題資料內有重複的單詞，且重複單詞應該計算多次，請各位注意 > 題目描述 > 給定n個模式串和1個文字串，求有多少個模式串在文字串裡出現過。 > 輸入輸出格式 > 輸入格式： > 第一行一個n，表示模式串個數； > 下面n行每行一個模式串； > 下面一行一個文字串。 > 輸出格式： > 一個數表示答案 > 輸入輸出樣例 > 輸入樣例#1： 複製 > 2 > a > aa > aa > 輸出樣例#1： 複製 > 2 > 說明 > subtask1[50pts]:∑length(模式串)<=10^6,length(文字串)<=10^6,n=1； > subtask2[50pts]:∑length(模式串)<=10^6,length(文字串)<=10^6； 就是模板題，下面給出模板： ```cpp #include #include #include #include using namespace std; struct node { int next[27]; int fail; int count; void init() { memset(next,-1,sizeof(next)); fail=0; count=0; } }s[1100001]; int i,j,k,m,n,o,p,js,jl,jk,len,ans,num; char str[1100000],des[1100000]; int q[1100000]; int ins() { int len=strlen(str+1); int ind=0,i,j; for(int i=1;i<=len;i++) { j=str[i]-'a'+1; if(s[ind].next[j]==-1) { num++; s[num].init(); s[ind].next[j]=num; } ind=s[ind].next[j]; } s[ind].count++; return 0; } int make_fail() { int head=1,tail=1; int inf,inf_f; for(int i=1;i<=26;i++) { if(s[0].next[i]!=-1) { q[tail]=s[0].next[i]; tail++; } } while(head0 && s[inf_f].next[i]==-1) inf_f=s[inf_f].fail; if(s[inf_f].next[i]!=-1)inf_f=s[inf_f].next[i]; s[s[inf].next[i]].fail=inf_f; } } head++; } return 0; } int find() { int len=strlen(des+1); int j,ind=0; for(int i=1;i<=len;i++) { j=des[i]-'a'+1; while(ind>0 && s[ind].next[j]==-1)ind=s[ind].fail; if(s[ind].next[j]!=-1) { ind=s[ind].next[j]; p=ind; while(p>0 && s[p].count!=-1) { ans=ans+s[p].count; s[p].count=-1; p=s[p].fail; } } } return 0; } int main() { scanf("%d",&m); num=0;s[0].init(); for(int i=1;i<=m;i++) { scanf("%s",str+1); ins(); } scanf("%s",des+1); ans=0; make_fail(); find(); printf("%d",ans); return 0; } ``` ## 結語 通過這篇部落格相信你一定已經學會了AC自動機！希望你喜歡這篇blog！！！