GAMES101系列筆記一 圖形學概述與線性代數入門
阿新 • • 發佈:2020-11-11
## 概述+線性代數
### 為什麼學習圖形學?
#### Computer Graphics is AWESOME!
主要涉及內容:
- 光柵化
- 曲線和網格
- 光線追蹤
- 動畫與模擬
Differences between CG and CV:
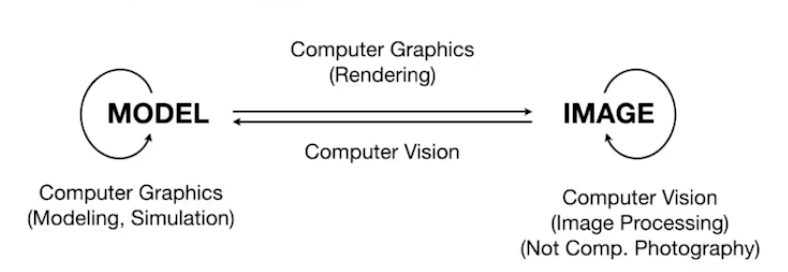
## 線性代數回顧
### 向量(Vectors)
- 方向和長度
模長:$||\vec{a}||$
- 沒有確定的起點
- 單位向量:模長為1
單位化向量: $\hat{a} = \vec{a}/||\vec{a}||$
- 向量求和:
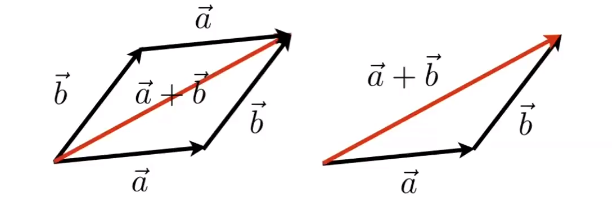
- 列向量,轉置,模長的計算方式
$\boldsymbol{A} = \begin{pmatrix}x \\ y\end{pmatrix} \quad \boldsymbol{A}^T = \begin{pmatrix}x&y\end{pmatrix} \quad ||\boldsymbol{A}|| = \sqrt{x^2+y^2}$
- 點乘(Dot/scalar Product)
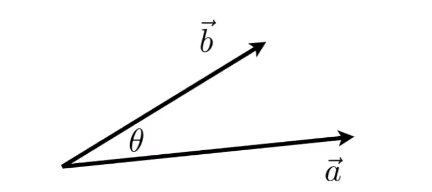
- 點乘定義:
$\vec{a} \cdot \vec{b} = ||\vec{a}||\,||\vec{b}||cos\theta$
$cos\theta = \frac{\vec{a}\cdot\vec{b}}{||\vec{a}\||\,||\vec{b}||}$
- For unit vectors:
$cos\theta = \hat{a}\cdot\hat{b}$
- 交換律、結合律、數乘
直角座標系下,計算更為方便:
- 2D:
$\vec{a}\cdot\vec{b} = \begin{pmatrix}x_a \\y_a\end{pmatrix}\cdot\begin{pmatrix}x_b \\y_b\end{pmatrix} = x_ax_b+y_ay_b.$
- 3D:
$\vec{a}\cdot\vec{b} = \begin{pmatrix}x_a \\y_a\\z_a\end{pmatrix}\cdot\begin{pmatrix}x_b \\y_b\\z_b\end{pmatrix} = x_ax_b+y_ay_b+z_az_b.$
- 投影:
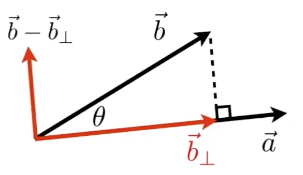
$\vec{b}_\perp:\vec{b}$ 在 $\vec{a}$ 上的投影;
$\vec{b}_\perp = k\hat{a};$
$k = ||\vec{b}_\perp|| = ||\vec{b}||cos\theta$
- 點乘可以告訴我們前和後的關係

- 叉乘(Cross\Vector product)
- 兩個向量相乘,得到一個與這兩個向量都相等的向量;
$\vec{a}\times\vec{b} = -\vec{b}\times\vec{a}$
$\vec{a}\times\vec{a} = \vec{0}$
$||\vec{a}\times\vec{b}|| = ||\vec{a}||\,||\vec{b}||sin\phi$
方向由右手螺旋定則確定

- 笛卡爾座標系下的計算方法:
$\vec{a}\times\vec{b} = \begin{pmatrix}y_az_b-y_bz_a \\ z_ax_b - x_az_b \\ x_ay_b-y_ax_b\end{pmatrix} = A*b = \begin{pmatrix}0 & -z_a& y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0\end{pmatrix}$
$A$ 為 $\vec{a}$ 的對偶矩陣。
- 叉乘在圖形學中的作用
判定左和右(一次叉乘),判斷內和外(三次叉乘)

- 正交系
- 三個單位向量
$ ||\vec{u}|| = ||\vec{v}|| = ||\vec{w}|| = 1$
- 兩兩垂直
$\vec{u}\cdot\vec{v} = \vec{v}\cdot\vec{w} = \vec{u}\cdot\vec{w}$
- 右手系
$\vec{w} = \vec{u}\times\vec{v}$
- 任何一個向量可以由這三個向量表示
$\vec{p} = (\vec{p}\cdot\vec{u})\vec{u} + (\vec{p}\cdot\vec{v})\vec{v} + (\vec{p}\cdot\vec{w})\vec{w}$
因為$\vec{u}\ \vec{v}\ \vec{w}$ 都是單位向量,所以可以用 $\vec{p}$ 在其上的投影乘以其本身來得到一個維度的分量。
- 矩陣(Matrices)
- 矩陣乘矩陣
維度需滿足:
$(M\times N)(N\times P) = (M\times P)$
(3 2)(2 4)= (3 4)

- 不符合交換律。但符合結合律和分配律。
$(AB)C = A(BC)$
$A(B+C) = AB + AC$
$(A+B)C = AC + BC$
- 矩陣向量乘
按 $y$ 軸映象
$\begin{pmatrix}-1 & 0 \\ 0 & 1\end{pmatrix}\begin{pmatrix}x \\ y \end{pmatrix} = \begin{pmatrix}-x \\ y\end{pmatrix}$
- 矩陣的轉置
$(AB)^T = B^TA^T$
- 單位矩陣
$I_{3\times3} = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1\end{pmatrix}$
$AA^{-1} = A^{-1}A = I;\quad (AB)^{-1} = B^{-1}A^{-1}$
- 向量乘法的矩陣形式
$\vec{a}\cdot\vec{b} = \vec{a}^T\vec{b}$
$\vec{a}\times\vec{b} = \begin{pmatrix}y_az_b-y_bz_a \\ z_ax_b - x_az_b \\ x_ay_b-y_ax_b\end{pmatrix} = A^*b = \begin{pmatrix}0 & -z_a& y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0\end{pm
