基於並查集的六度分隔理論的驗證與實現
阿新 • • 發佈:2021-01-22
>首發於微信公眾號:幾何思維
### 1.六度分隔理論
**世界上任何兩個互不相識的人,最多隻需要通過6箇中間人,就可以建立聯絡。**
哈佛大學的社會心理學家米爾格蘭姆於1967設計了一個連鎖信件實驗。他將一套連鎖信件隨機發送給居住在內布拉斯加州奧馬哈的160個人,信中放了一個波士頓股票經紀人的名字,並要求每名收信人把這封信寄給自己認為是比較接近這名股票經紀人的朋友。這位朋友收到信後,再把信寄給他認為更接近這名股票經紀人的朋友。最終,大部分信件都寄到了這名股票經紀人手中,每封信平均經手6次到達。
例如你認識老王,老王認識李大爺,李大爺又認識某人,如此關聯,你和奧巴馬之間,最多隻差6個人介紹就可以加微信好友啦。
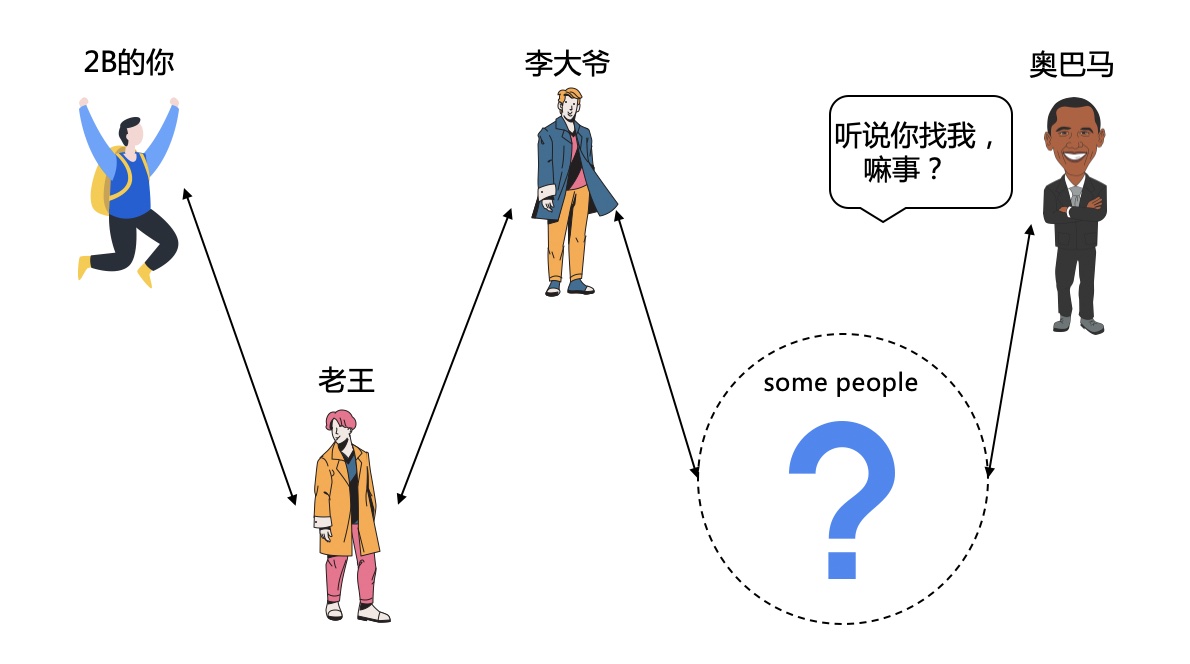
 那麼問題來了,人口普查哪家強,四川成都找老王。。。
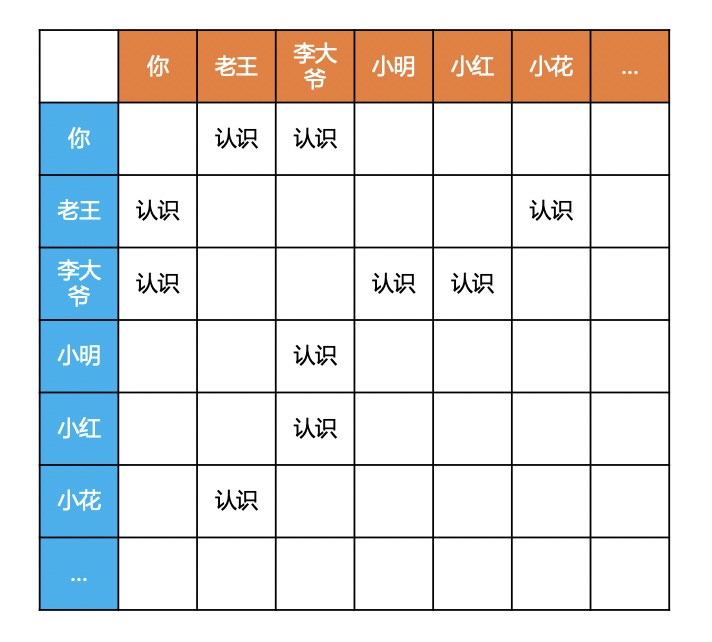
所有的資訊資料如下表:
那麼問題來了,人口普查哪家強,四川成都找老王。。。
所有的資訊資料如下表:
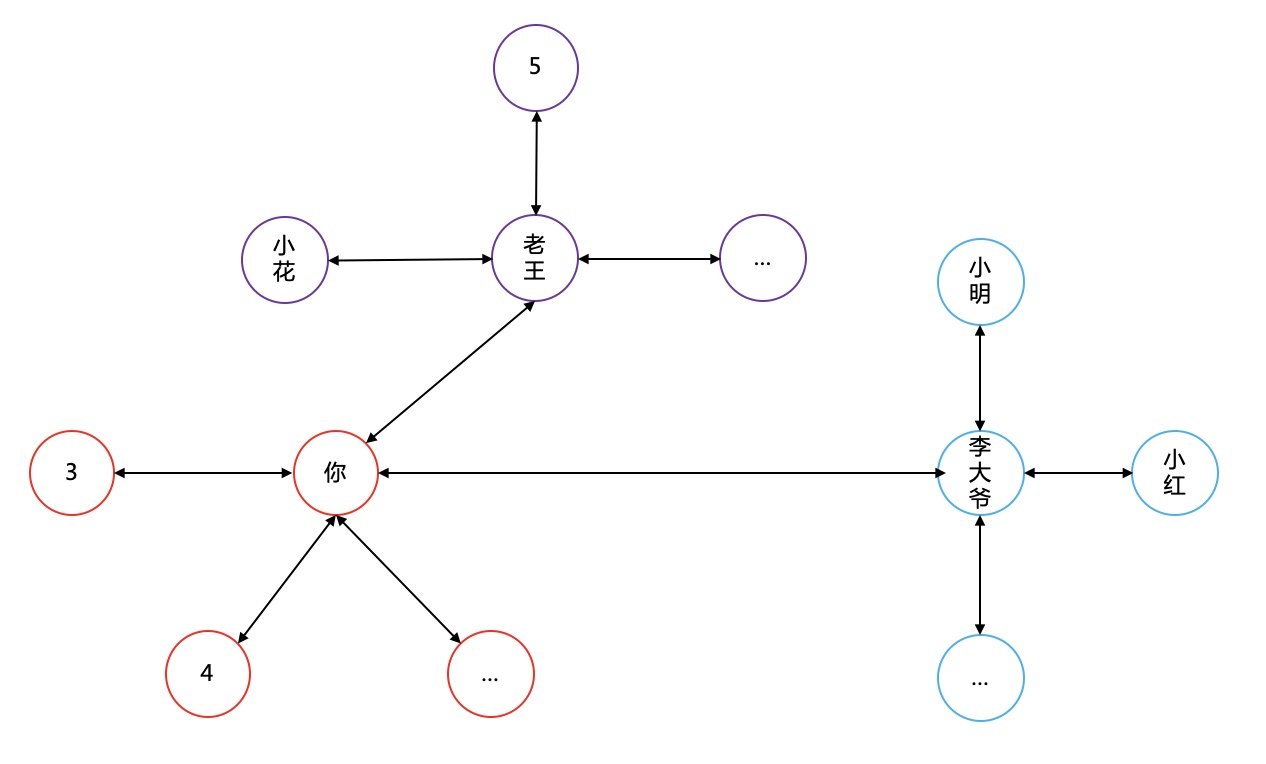
 轉換成圖的形式會比較直觀。如果把2個互相認識的人用線連線起來,問題就轉化成:你和老奧之間能否找到一條通路(暫不考慮最短是不是不超過6個人)。
轉換成圖的形式會比較直觀。如果把2個互相認識的人用線連線起來,問題就轉化成:你和老奧之間能否找到一條通路(暫不考慮最短是不是不超過6個人)。
 ### 3.問題建模
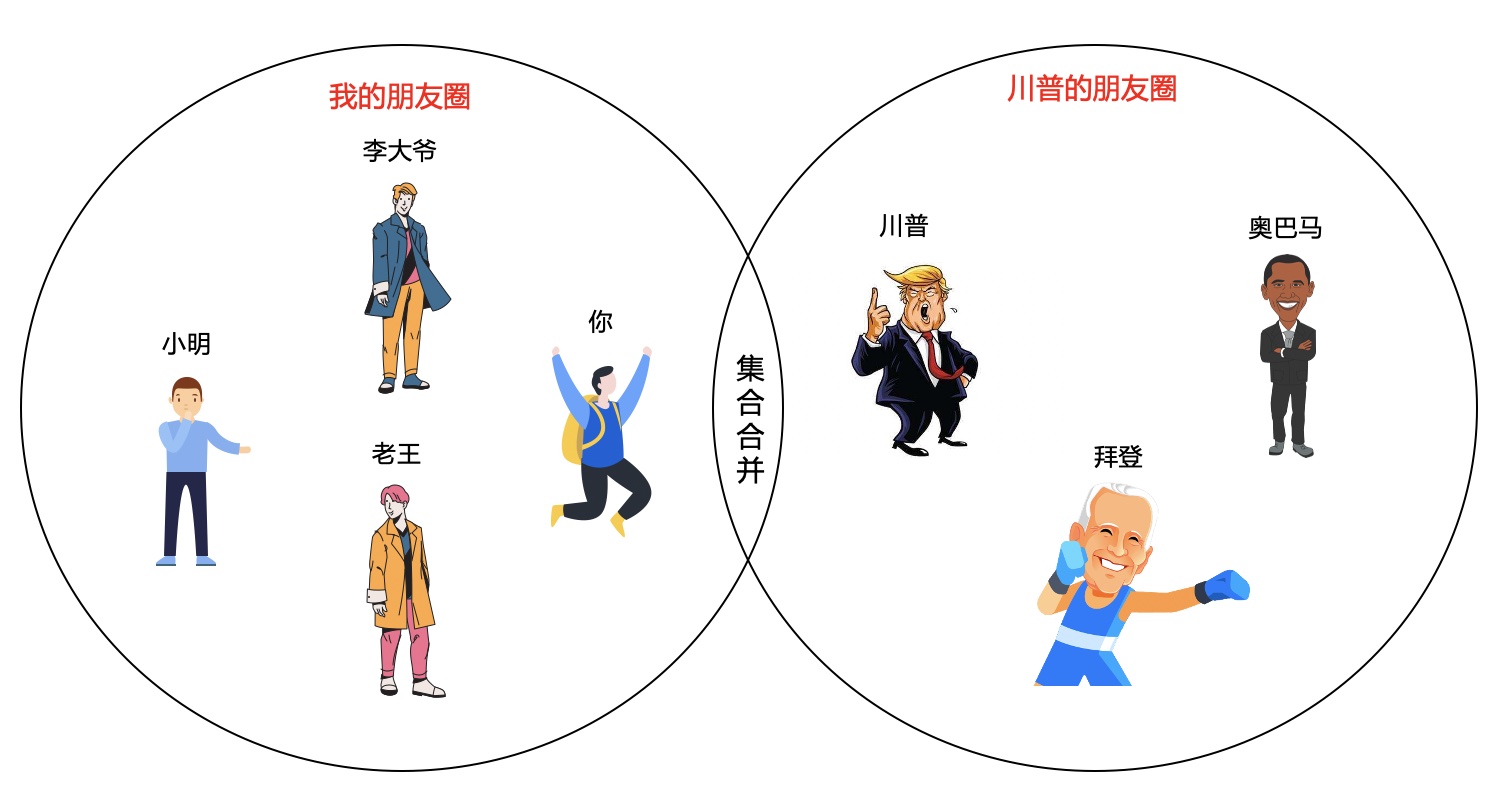
假設**朋友的朋友都是朋友,朋友的敵人也是朋友**(或者敵人的朋友還是朋友,whatever...)。
我們把所有直接認識的,或者能間接認識的都放到一個大集合中,建立一個大朋友圈。
問題就變成:老奧在不在我們的大朋友圈裡?
### 3.問題建模
假設**朋友的朋友都是朋友,朋友的敵人也是朋友**(或者敵人的朋友還是朋友,whatever...)。
我們把所有直接認識的,或者能間接認識的都放到一個大集合中,建立一個大朋友圈。
問題就變成:老奧在不在我們的大朋友圈裡?

 相信敏銳的你已經發現問題的本質,這裡面只有2個重要的操作,來跟我一起大聲朗讀,**並...查...**。這就需要一種能高效處理集合的合併與查詢的演算法,並查集就是專門為這種場景量身定製。
相信敏銳的你已經發現問題的本質,這裡面只有2個重要的操作,來跟我一起大聲朗讀,**並...查...**。這就需要一種能高效處理集合的合併與查詢的演算法,並查集就是專門為這種場景量身定製。
 ### 4.演算法理論
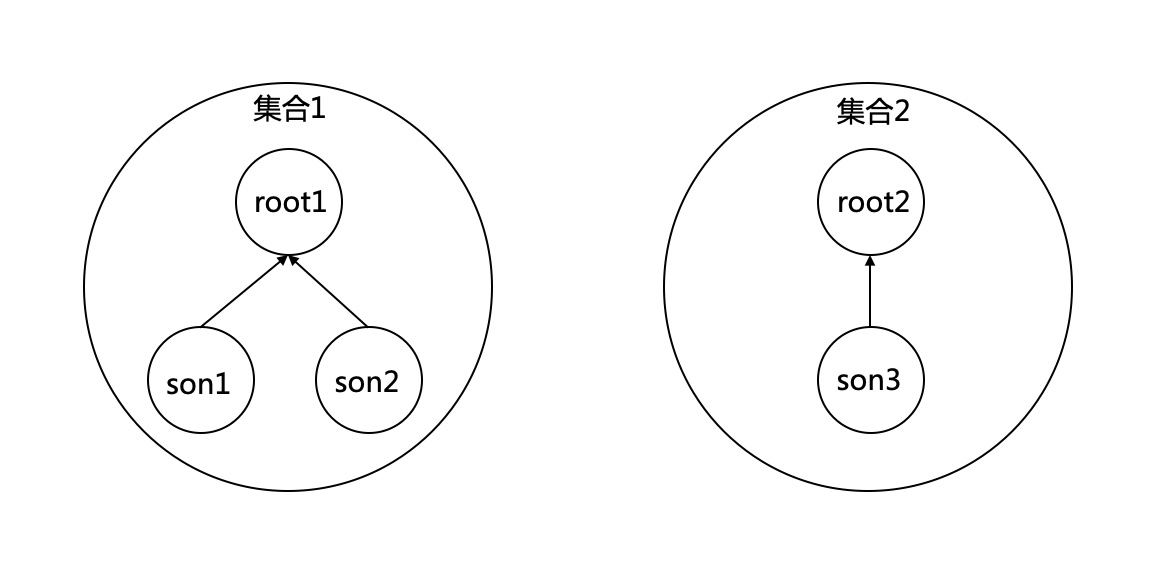
>**並查集本質是一個森林,裡面有很多樹。**
每個樹有一個根,以不同的根代表不同的集合。如下,root1,root2代表兩個集合。
### 4.演算法理論
>**並查集本質是一個森林,裡面有很多樹。**
每個樹有一個根,以不同的根代表不同的集合。如下,root1,root2代表兩個集合。
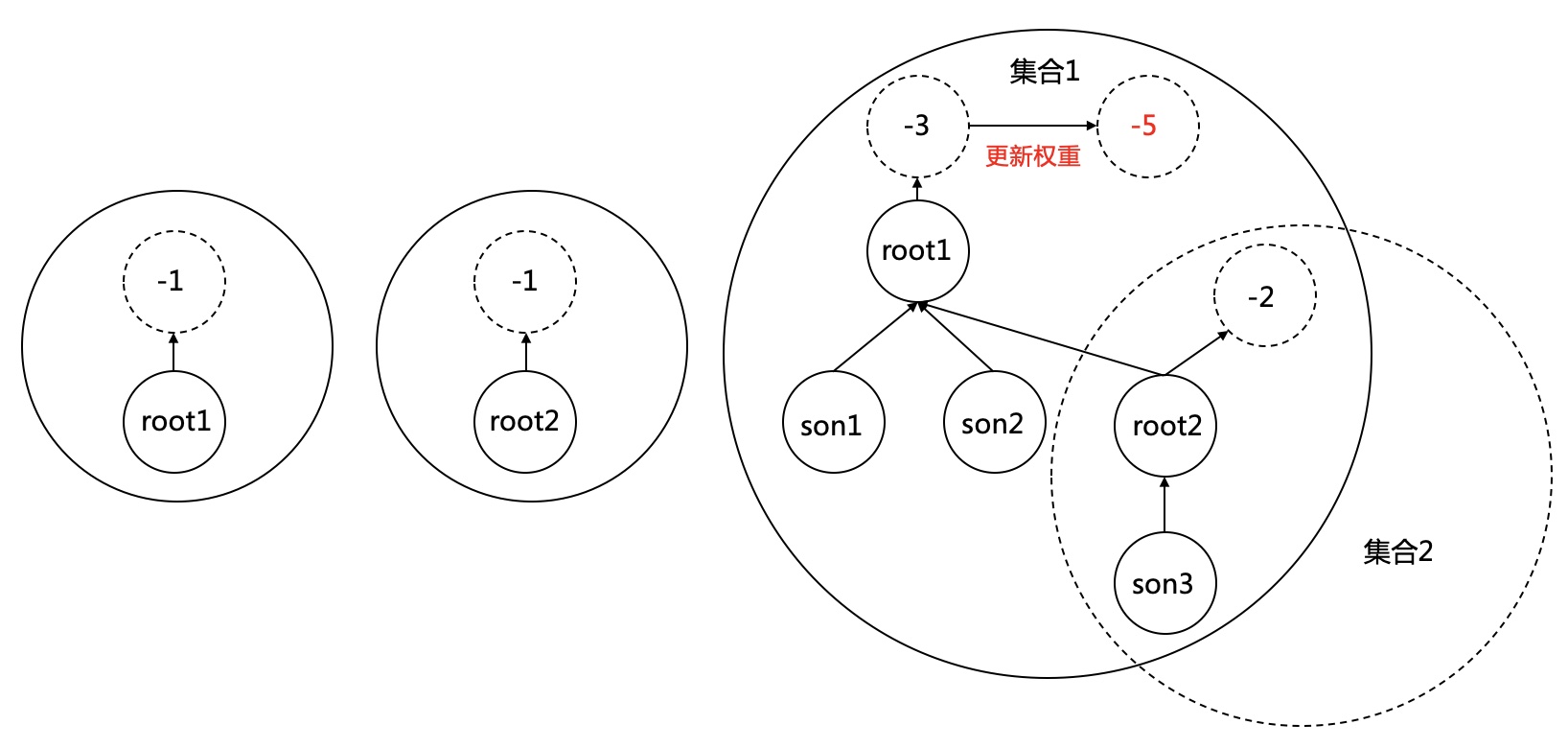
 初始時,每個元素都屬於一個獨立的集合,該元素作為根。每個根指向一個虛擬根-n,代表權重(表示該集合有n個元素)。
**更新合併**
將權重小的集合的根指向權重大的集合的根(此操作是為儘量降低樹的深度)。
初始時,每個元素都屬於一個獨立的集合,該元素作為根。每個根指向一個虛擬根-n,代表權重(表示該集合有n個元素)。
**更新合併**
將權重小的集合的根指向權重大的集合的根(此操作是為儘量降低樹的深度)。
 ### 5.程式碼實現
**查詢**
```cpp
int findFather(int s) {
int root = s, temp;
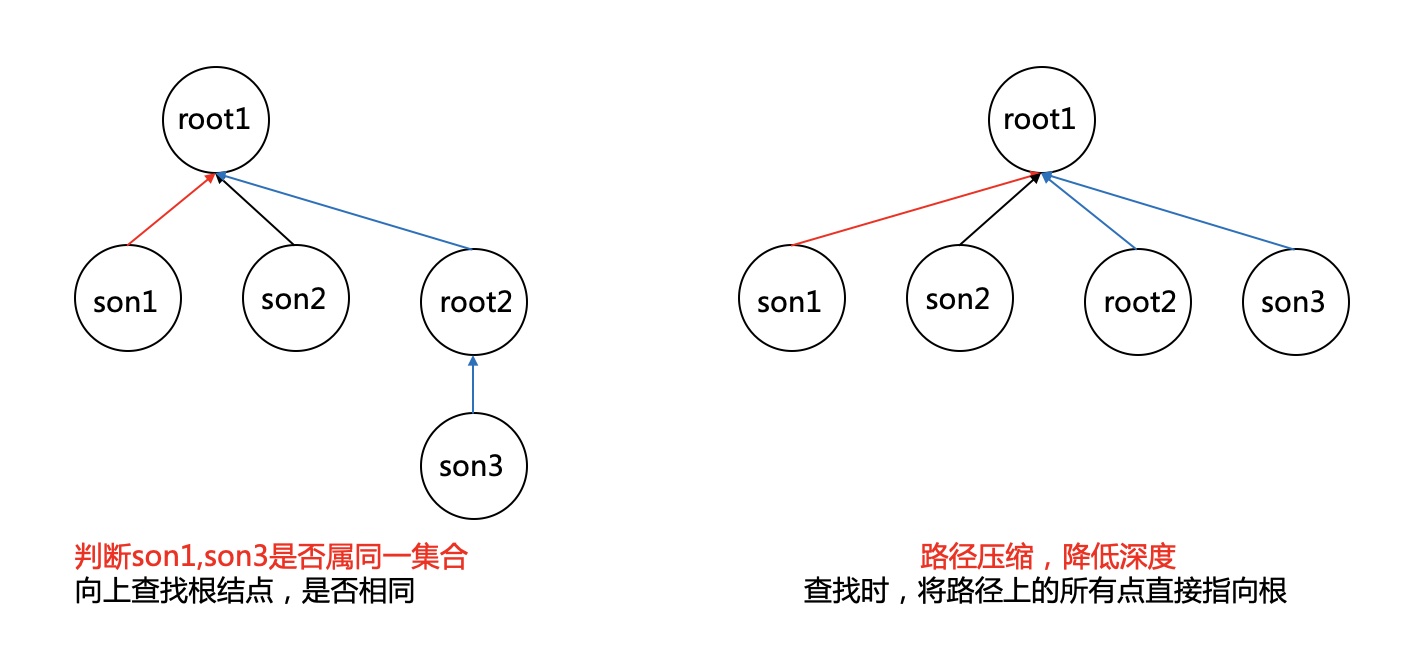
// 查詢s的最頂層根
while (father[root] >= 0) {
root = father[root];
}
// 路徑壓縮,提高後續查詢效率
while (s != root) {
temp = father[s];
father[s] = root;
s = temp;
}
return root;
}
```
**合併**
```cpp
void unionSet(int s, int e) {
int rootS = findFather(s);
int rootE = findFather(e);
int weight = father[rootS] + father[rootE];
// 將結點數少的集合作為結點數多的集合的兒子節點
if (father[rootS] > father[rootE]) {
father[rootS] = rootE;
father[rootE] = weight;
} else {
father[rootE] = rootS;
father[rootS] = weight;
}
}
```
例題,poj1182,poj1308,poj1456,poj1611
**掃描下方二維碼關注公眾號,第一時間獲取更新資訊!**
### 5.程式碼實現
**查詢**
```cpp
int findFather(int s) {
int root = s, temp;
// 查詢s的最頂層根
while (father[root] >= 0) {
root = father[root];
}
// 路徑壓縮,提高後續查詢效率
while (s != root) {
temp = father[s];
father[s] = root;
s = temp;
}
return root;
}
```
**合併**
```cpp
void unionSet(int s, int e) {
int rootS = findFather(s);
int rootE = findFather(e);
int weight = father[rootS] + father[rootE];
// 將結點數少的集合作為結點數多的集合的兒子節點
if (father[rootS] > father[rootE]) {
father[rootS] = rootE;
father[rootE] = weight;
} else {
father[rootE] = rootS;
father[rootS] = weight;
}
}
```
例題,poj1182,poj1308,poj1456,poj1611
**掃描下方二維碼關注公眾號,第一時間獲取更新資訊!**


 那麼問題來了,人口普查哪家強,四川成都找老王。。。
所有的資訊資料如下表:
那麼問題來了,人口普查哪家強,四川成都找老王。。。
所有的資訊資料如下表:
 轉換成圖的形式會比較直觀。如果把2個互相認識的人用線連線起來,問題就轉化成:你和老奧之間能否找到一條通路(暫不考慮最短是不是不超過6個人)。
轉換成圖的形式會比較直觀。如果把2個互相認識的人用線連線起來,問題就轉化成:你和老奧之間能否找到一條通路(暫不考慮最短是不是不超過6個人)。
 ### 3.問題建模
假設**朋友的朋友都是朋友,朋友的敵人也是朋友**(或者敵人的朋友還是朋友,whatever...)。
我們把所有直接認識的,或者能間接認識的都放到一個大集合中,建立一個大朋友圈。
問題就變成:老奧在不在我們的大朋友圈裡?
### 3.問題建模
假設**朋友的朋友都是朋友,朋友的敵人也是朋友**(或者敵人的朋友還是朋友,whatever...)。
我們把所有直接認識的,或者能間接認識的都放到一個大集合中,建立一個大朋友圈。
問題就變成:老奧在不在我們的大朋友圈裡?

 相信敏銳的你已經發現問題的本質,這裡面只有2個重要的操作,來跟我一起大聲朗讀,**並...查...**。這就需要一種能高效處理集合的合併與查詢的演算法,並查集就是專門為這種場景量身定製。
相信敏銳的你已經發現問題的本質,這裡面只有2個重要的操作,來跟我一起大聲朗讀,**並...查...**。這就需要一種能高效處理集合的合併與查詢的演算法,並查集就是專門為這種場景量身定製。
 ### 4.演算法理論
>**並查集本質是一個森林,裡面有很多樹。**
每個樹有一個根,以不同的根代表不同的集合。如下,root1,root2代表兩個集合。
### 4.演算法理論
>**並查集本質是一個森林,裡面有很多樹。**
每個樹有一個根,以不同的根代表不同的集合。如下,root1,root2代表兩個集合。
 初始時,每個元素都屬於一個獨立的集合,該元素作為根。每個根指向一個虛擬根-n,代表權重(表示該集合有n個元素)。
**更新合併**
將權重小的集合的根指向權重大的集合的根(此操作是為儘量降低樹的深度)。
初始時,每個元素都屬於一個獨立的集合,該元素作為根。每個根指向一個虛擬根-n,代表權重(表示該集合有n個元素)。
**更新合併**
將權重小的集合的根指向權重大的集合的根(此操作是為儘量降低樹的深度)。

 ### 5.程式碼實現
**查詢**
```cpp
int findFather(int s) {
int root = s, temp;
// 查詢s的最頂層根
while (father[root] >= 0) {
root = father[root];
}
// 路徑壓縮,提高後續查詢效率
while (s != root) {
temp = father[s];
father[s] = root;
s = temp;
}
return root;
}
```
**合併**
```cpp
void unionSet(int s, int e) {
int rootS = findFather(s);
int rootE = findFather(e);
int weight = father[rootS] + father[rootE];
// 將結點數少的集合作為結點數多的集合的兒子節點
if (father[rootS] > father[rootE]) {
father[rootS] = rootE;
father[rootE] = weight;
} else {
father[rootE] = rootS;
father[rootS] = weight;
}
}
```
例題,poj1182,poj1308,poj1456,poj1611
**掃描下方二維碼關注公眾號,第一時間獲取更新資訊!**
### 5.程式碼實現
**查詢**
```cpp
int findFather(int s) {
int root = s, temp;
// 查詢s的最頂層根
while (father[root] >= 0) {
root = father[root];
}
// 路徑壓縮,提高後續查詢效率
while (s != root) {
temp = father[s];
father[s] = root;
s = temp;
}
return root;
}
```
**合併**
```cpp
void unionSet(int s, int e) {
int rootS = findFather(s);
int rootE = findFather(e);
int weight = father[rootS] + father[rootE];
// 將結點數少的集合作為結點數多的集合的兒子節點
if (father[rootS] > father[rootE]) {
father[rootS] = rootE;
father[rootE] = weight;
} else {
father[rootE] = rootS;
father[rootS] = weight;
}
}
```
例題,poj1182,poj1308,poj1456,poj1611
**掃描下方二維碼關注公眾號,第一時間獲取更新資訊!**

