簡單易懂的並查集演算法以及並查集實戰演練
阿新 • • 發佈:2021-01-31
[TOC](文章目錄)
# 前言 並查集演算法適用於處理一些不相交集合的合併及查詢問題。對於這一類的問題使用並查集,不但節省了空間,而且大大縮短了執行時間。 基本的並查集很好寫出一個模板,對於一些特殊的題目也能很好對並查集進行變形,接下來來看一下引例瞭解一下並查集
# 一、引例 男生寢室關係錯綜複雜,甚至一個四人寢室都能整出四個爸爸四個兒子。 有一天宿管阿姨想知道這個寢室樓裡有多少個爸爸家族,但是宿管只知道哪兩個人互稱爸爸。 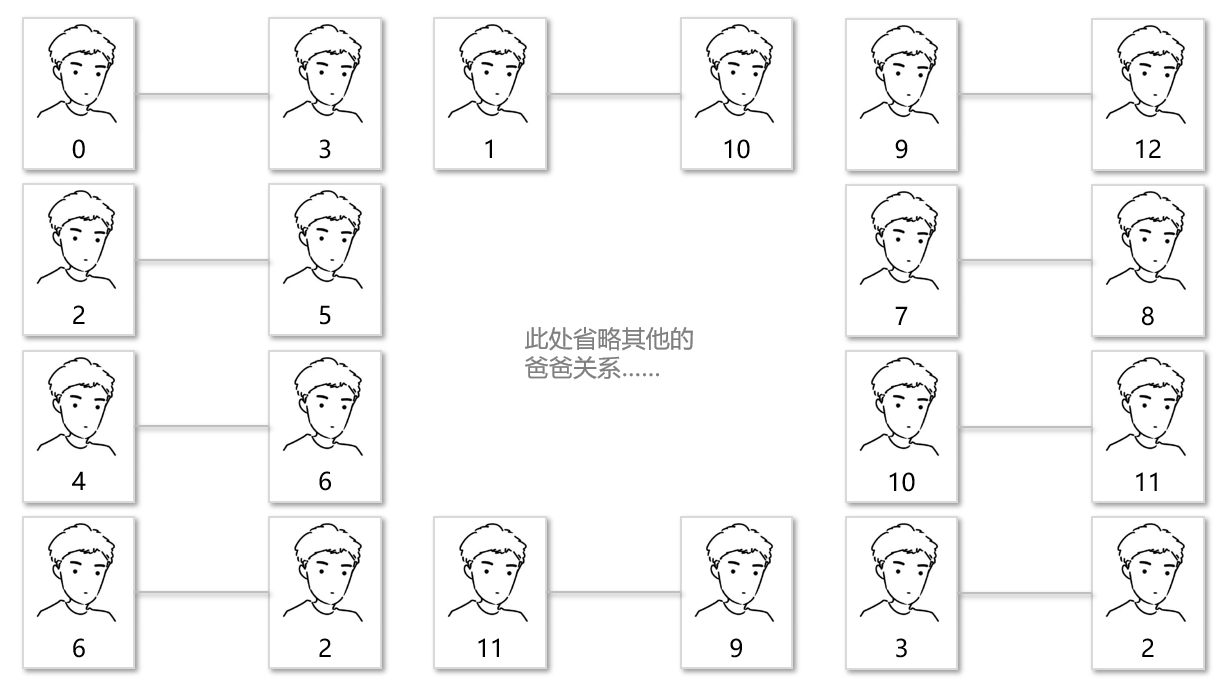 上圖是宿管阿姨花了三天三夜整理的爸爸關係圖,宿舍樓裡總共有n個男生,所以她將每個男生編號0~(n-1)。剛開始人不多,所以阿姨想看0和6是不是一個家族的,只需要看這幾個關係即可知道0和6是一個爸爸家族的  後來學生知道了,紛紛來宿管這兒查關係,想看看自己有多少個兒子,自己和隔壁班的學霸是不是爸爸關係。 這一下可給宿管忙壞了,有時候得追溯到十幾個人才能確定兩個人有爸爸關係,而且還會查錯走不少彎路,於是阿姨花了一個晚上,硬生生把關係無向圖給畫出來了,這下子學生一看圖就能知道自己在爸爸家族有多少兒子。 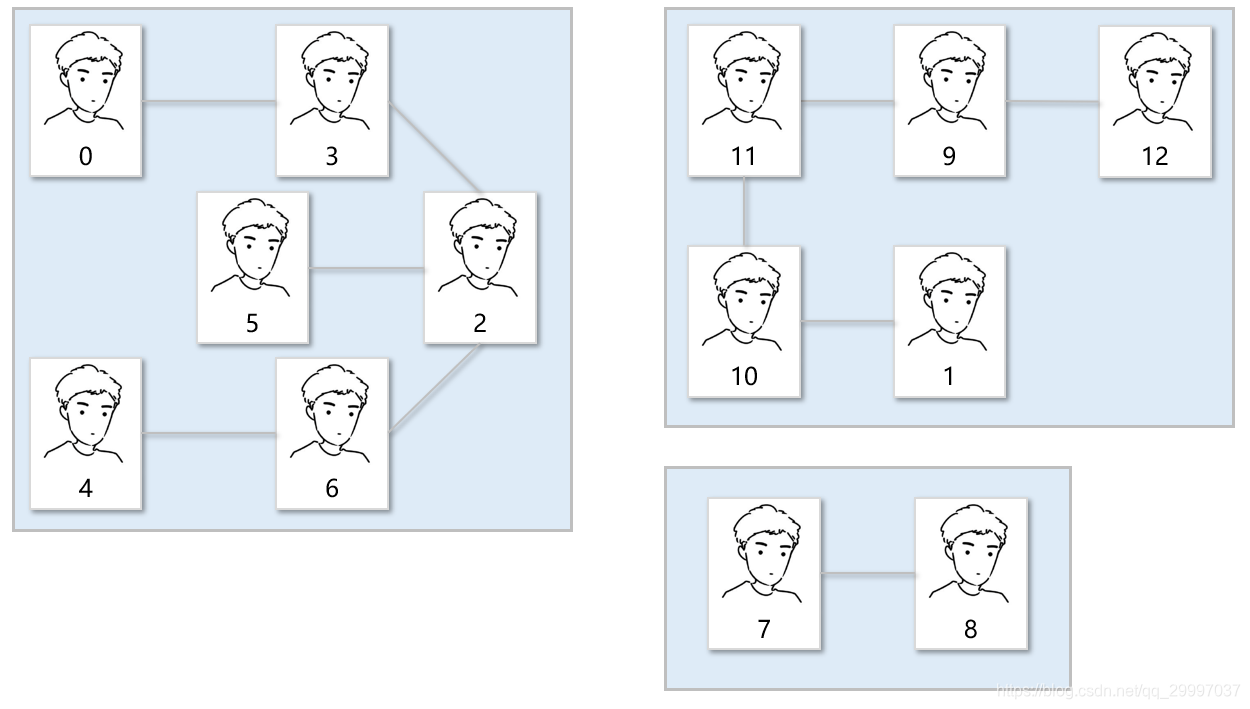 時間一長,學生跑來和宿管講:“阿姨阿姨,我又有新兒子了,我是0,我兒子是7”,於是阿姨在圖上簡單地畫一下,一個新關係圖出來了  # 二、結合引例寫出並查集 ## 1. 並查集維護一個數組 說來你可能不信,以上就是並查集的思路了!下面我們迴歸正題,在上面例子中,我們涉及到了兩個操作,一個是**查詢**,一個是**合併**,這也是並查集名字的由來。 在這裡我們新建一個數組arr,圖示第一行為座標i,第二行為陣列元素的內容arr[i],陣列座標就是學生的編號,分別是0, 1, 2, ..., n-1。arr[x]的值表示編號為x的同學的爸爸是誰。初始值表示自己就是自己的爸爸,所以arr[x]=x。  ## 2. 並查集的 並 操作 接下來一個“父子關係”加入了,0說3是兒子,3說0是兒子,誰也爭持不下,那就偷偷的規定右邊是左邊的爸爸,不告訴他們。(你可能會疑惑,為什麼要這樣規定,可以反過來嗎?後面會做出解釋,你姑且先放一邊哈)  接下來迴圈往復,重複以上操作,依次將2與5,4與6合併  我們通過對陣列元素的修改,得到了一個集合,我們可以用無向圖來表示。按照0的爸爸是3,3的爸爸是4,4的爸爸是6等這樣來把它們連起來  ## 3. 並查集的 查 操作 我們要查詢0和4是不是一個家族的,就需要檢視0的祖先和4的祖先是同一個人嗎?換句話說也就是隻需要向上依次查詢0的爸爸的爸爸的爸爸,查詢4的爸爸的爸爸的爸爸,直到最後的爸爸的爸爸是他自己,就說明這個是爸爸家族裡的祖先。下面給出圖示說明  做出一點解釋,對於第一步,因為陣列arr對應的arr[x]=y,表示編號為x的人的爸爸是y,所以要想知道x的父親,必須訪問arr[x]即可知道 對於第二步,祖先一定滿足arr[x]=x,即爸爸的爸爸是自己,所以只要不滿足arr[x]=x的,一定x一定還有爺爺,這時候就要一直向上查詢x的爺爺爺爺爺爺爺爺,直到第六步所示,arr[6]=6表示6是祖先!我們找到了!! ## 4. 基本並查集模板程式碼實現——第一版(有錯誤後面分析) 這樣一來,我們簡單地得到了第一版的並查集: ```java /** * @author 太白 */ public class UnionFind { private int[] arr; public UnionFind(int size) { arr = new int[size]; for (int i = 0; i < size; i++) { arr[i] = i; // 初始化,每個人是自己的父親,即每個人都是祖先 } } public int find(int son) { int father = arr[son]; // 迴圈,直到爸爸的爸爸是自己為止 while (father != arr[father]) { father = arr[father]; } return father; } public void union(int son1, int son2) { // 此處有錯誤,可以思考一下,下面我們舉例說明為什麼錯了 arr[son1] = son2; // 合併,son1的爸爸是son2 } } ``` ## 5. 一個錯誤 我們給出一種情況,我們加了一個新關係,0的爸爸是2,來看看我們現在的程式碼是否能完成預期功能  完蛋!由於我們在union方法中只是進行`arr[son1]=son2;`導致原先的祖爺爺6少了一個孫子0,孫子0歸祖爺爺5去了,簡直是背盟敗約,跑到了別的爸爸家族裡面去了!!! 沒事,其實解決方法特別簡單!別被這個小錯誤給亂了陣腳,這也是起初學該演算法容易犯的錯誤,可以注意一下。 我們維護的是m個爸爸家族,所以如果我們將整個爸爸家族當做是一個人,另一個爸爸家族當做是另一個人,再讓這兩個巨大的人互認爸爸兒子即可。自然,我們肯定會讓祖爺爺出面,去和另一個家族比拼,誰贏了就誰當爸爸。(當然無所謂誰當,後面會解釋) 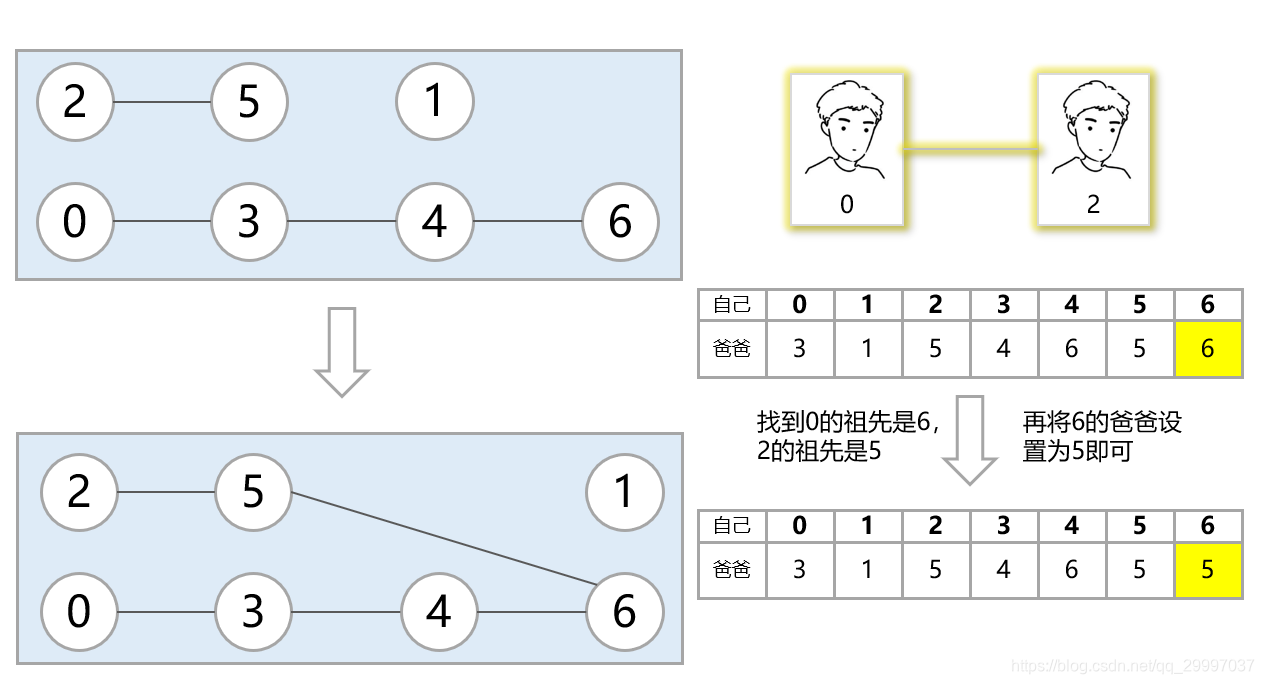 ## 6. 基本並查集模板程式碼實現——第二版(解決錯誤) 現在,我們給出第二版,解決了上述的BUG,你會看到解決方式是如此的簡單,程式碼也很好理解,找到雙方的祖先,最後讓son2的祖先當son1祖先的爸爸。 ```java /** * @author 太白 */ public class UnionFind { private int[] arr; public UnionFind(int size) { arr = new int[size]; for (int i = 0; i < size; i++) { arr[i] = i; } } public int find(int son) { int father = arr[son]; while (father != arr[father]) { father = arr[father]; } return father; } public void union(int son1, int son2) { // 請相信我,只改動了這裡,其他地方都沒有修改過 int father1 = find(son1); int father2 = find(son2); // 注意中括號裡面的son改成了father arr[father1] = father2; } } ``` ## 7. 一點點解釋,為什麼無需在意誰是誰的爸爸 在上面我們的程式碼中默認了都是son1的爸爸是son2,那我們可以讓son2的爸爸是son1嗎?答案是可以! 因為我們維護的是集合,只是確認一個集合裡有誰即可。 從語義上講:今天你是我爸爸,明天我是你爸爸,但是我們依然是一個爸爸家族裡的一員,所以不需要在意誰是誰的爸爸。 從家族結構來講:整個家族就是一個無向圖,關係是雙向的。0可以是3的爸爸,3也可以是0的爸爸,所以無需刻意要求,當然也可以在程式碼裡反著寫`arr[father2]=father1`
# 三、並查集的優化 ## 1. 並查集優化原理 可以看到我們每次查詢都得一個一個向上查,0的爸爸是3,3的爸爸是4,4的爸爸是6,6的爸爸是6...如果我們資料量大一點,一個宿舍樓上萬人,那麼我們每次查詢最大可能得查上萬次,這太花時間啦!那麼我們能不能做出一點改進呢?誒你別說,還真有~ 思路是這樣的,畢竟我們每次都得查詢x的祖先是誰,不關心x的爸爸是誰,x的爺爺是誰,那為什麼不直接讓arr[x]指向它的祖先編號y呢,在本例中我們為什麼不讓arr[0]=6, arr[3]=6, arr[4]=6呢? 所以我們在本例中,可以讓0、3、4的爸爸直接認定為6即可。延續上一次的查詢,我們再多一項功能就是**再次遍歷**0的爸爸3、4,讓3和4的爸爸設定為6  ## 2. 基本並查集模板程式碼實現——第三版(優化) 程式碼實現也很簡單,我們只需要在find方法中加個四五行即可 ```java /** * @author 太白 */ public class UnionFind { private int[] arr; public UnionFind(int size) { arr = new int[size]; for (int i = 0; i < size; i++) { arr[i] = i; } } public int find(int son) { int father = arr[son]; while (father != arr[father]) { father = arr[father]; } // 直到迴圈到祖先為止 while (father != arr[son]) { // 儲存當前son的爸爸 // 因為要更改son的爸爸,所以要有個備份 int next = arr[son]; // 將son的爸爸改成father arr[son] = father; // 找到下一個爸爸(用備份的爸爸賦值給son即可) // 將son改成下一個爸爸,為下一個迴圈做準備 son = next; } return father; } public void union(int son1, int son2) { int father1 = find(son1); int father2 = find(son2); arr[father1] = father2; } } ``` 於是,我們的模板就算是做好了,我習慣在裡面新增兩個方法,一個是`isFamily(int, int)`,另一個是`getCategory()`,第一個可以檢測兩個人是不是同一個爸爸家族的成員,另外一個看看總共有多少個爸爸家族,這兩個方法經常在題目中用到,也很好實現,所以後續我們會結合例題,看如何十分簡單地運用該演算法解決一些相對複雜的題目。
# 四、例題 未完
# 前言 並查集演算法適用於處理一些不相交集合的合併及查詢問題。對於這一類的問題使用並查集,不但節省了空間,而且大大縮短了執行時間。 基本的並查集很好寫出一個模板,對於一些特殊的題目也能很好對並查集進行變形,接下來來看一下引例瞭解一下並查集
# 一、引例 男生寢室關係錯綜複雜,甚至一個四人寢室都能整出四個爸爸四個兒子。 有一天宿管阿姨想知道這個寢室樓裡有多少個爸爸家族,但是宿管只知道哪兩個人互稱爸爸。  上圖是宿管阿姨花了三天三夜整理的爸爸關係圖,宿舍樓裡總共有n個男生,所以她將每個男生編號0~(n-1)。剛開始人不多,所以阿姨想看0和6是不是一個家族的,只需要看這幾個關係即可知道0和6是一個爸爸家族的  後來學生知道了,紛紛來宿管這兒查關係,想看看自己有多少個兒子,自己和隔壁班的學霸是不是爸爸關係。 這一下可給宿管忙壞了,有時候得追溯到十幾個人才能確定兩個人有爸爸關係,而且還會查錯走不少彎路,於是阿姨花了一個晚上,硬生生把關係無向圖給畫出來了,這下子學生一看圖就能知道自己在爸爸家族有多少兒子。  時間一長,學生跑來和宿管講:“阿姨阿姨,我又有新兒子了,我是0,我兒子是7”,於是阿姨在圖上簡單地畫一下,一個新關係圖出來了  # 二、結合引例寫出並查集 ## 1. 並查集維護一個數組 說來你可能不信,以上就是並查集的思路了!下面我們迴歸正題,在上面例子中,我們涉及到了兩個操作,一個是**查詢**,一個是**合併**,這也是並查集名字的由來。 在這裡我們新建一個數組arr,圖示第一行為座標i,第二行為陣列元素的內容arr[i],陣列座標就是學生的編號,分別是0, 1, 2, ..., n-1。arr[x]的值表示編號為x的同學的爸爸是誰。初始值表示自己就是自己的爸爸,所以arr[x]=x。  ## 2. 並查集的 並 操作 接下來一個“父子關係”加入了,0說3是兒子,3說0是兒子,誰也爭持不下,那就偷偷的規定右邊是左邊的爸爸,不告訴他們。(你可能會疑惑,為什麼要這樣規定,可以反過來嗎?後面會做出解釋,你姑且先放一邊哈)  接下來迴圈往復,重複以上操作,依次將2與5,4與6合併  我們通過對陣列元素的修改,得到了一個集合,我們可以用無向圖來表示。按照0的爸爸是3,3的爸爸是4,4的爸爸是6等這樣來把它們連起來  ## 3. 並查集的 查 操作 我們要查詢0和4是不是一個家族的,就需要檢視0的祖先和4的祖先是同一個人嗎?換句話說也就是隻需要向上依次查詢0的爸爸的爸爸的爸爸,查詢4的爸爸的爸爸的爸爸,直到最後的爸爸的爸爸是他自己,就說明這個是爸爸家族裡的祖先。下面給出圖示說明  做出一點解釋,對於第一步,因為陣列arr對應的arr[x]=y,表示編號為x的人的爸爸是y,所以要想知道x的父親,必須訪問arr[x]即可知道 對於第二步,祖先一定滿足arr[x]=x,即爸爸的爸爸是自己,所以只要不滿足arr[x]=x的,一定x一定還有爺爺,這時候就要一直向上查詢x的爺爺爺爺爺爺爺爺,直到第六步所示,arr[6]=6表示6是祖先!我們找到了!! ## 4. 基本並查集模板程式碼實現——第一版(有錯誤後面分析) 這樣一來,我們簡單地得到了第一版的並查集: ```java /** * @author 太白 */ public class UnionFind { private int[] arr; public UnionFind(int size) { arr = new int[size]; for (int i = 0; i < size; i++) { arr[i] = i; // 初始化,每個人是自己的父親,即每個人都是祖先 } } public int find(int son) { int father = arr[son]; // 迴圈,直到爸爸的爸爸是自己為止 while (father != arr[father]) { father = arr[father]; } return father; } public void union(int son1, int son2) { // 此處有錯誤,可以思考一下,下面我們舉例說明為什麼錯了 arr[son1] = son2; // 合併,son1的爸爸是son2 } } ``` ## 5. 一個錯誤 我們給出一種情況,我們加了一個新關係,0的爸爸是2,來看看我們現在的程式碼是否能完成預期功能  完蛋!由於我們在union方法中只是進行`arr[son1]=son2;`導致原先的祖爺爺6少了一個孫子0,孫子0歸祖爺爺5去了,簡直是背盟敗約,跑到了別的爸爸家族裡面去了!!! 沒事,其實解決方法特別簡單!別被這個小錯誤給亂了陣腳,這也是起初學該演算法容易犯的錯誤,可以注意一下。 我們維護的是m個爸爸家族,所以如果我們將整個爸爸家族當做是一個人,另一個爸爸家族當做是另一個人,再讓這兩個巨大的人互認爸爸兒子即可。自然,我們肯定會讓祖爺爺出面,去和另一個家族比拼,誰贏了就誰當爸爸。(當然無所謂誰當,後面會解釋)  ## 6. 基本並查集模板程式碼實現——第二版(解決錯誤) 現在,我們給出第二版,解決了上述的BUG,你會看到解決方式是如此的簡單,程式碼也很好理解,找到雙方的祖先,最後讓son2的祖先當son1祖先的爸爸。 ```java /** * @author 太白 */ public class UnionFind { private int[] arr; public UnionFind(int size) { arr = new int[size]; for (int i = 0; i < size; i++) { arr[i] = i; } } public int find(int son) { int father = arr[son]; while (father != arr[father]) { father = arr[father]; } return father; } public void union(int son1, int son2) { // 請相信我,只改動了這裡,其他地方都沒有修改過 int father1 = find(son1); int father2 = find(son2); // 注意中括號裡面的son改成了father arr[father1] = father2; } } ``` ## 7. 一點點解釋,為什麼無需在意誰是誰的爸爸 在上面我們的程式碼中默認了都是son1的爸爸是son2,那我們可以讓son2的爸爸是son1嗎?答案是可以! 因為我們維護的是集合,只是確認一個集合裡有誰即可。 從語義上講:今天你是我爸爸,明天我是你爸爸,但是我們依然是一個爸爸家族裡的一員,所以不需要在意誰是誰的爸爸。 從家族結構來講:整個家族就是一個無向圖,關係是雙向的。0可以是3的爸爸,3也可以是0的爸爸,所以無需刻意要求,當然也可以在程式碼裡反著寫`arr[father2]=father1`
# 三、並查集的優化 ## 1. 並查集優化原理 可以看到我們每次查詢都得一個一個向上查,0的爸爸是3,3的爸爸是4,4的爸爸是6,6的爸爸是6...如果我們資料量大一點,一個宿舍樓上萬人,那麼我們每次查詢最大可能得查上萬次,這太花時間啦!那麼我們能不能做出一點改進呢?誒你別說,還真有~ 思路是這樣的,畢竟我們每次都得查詢x的祖先是誰,不關心x的爸爸是誰,x的爺爺是誰,那為什麼不直接讓arr[x]指向它的祖先編號y呢,在本例中我們為什麼不讓arr[0]=6, arr[3]=6, arr[4]=6呢? 所以我們在本例中,可以讓0、3、4的爸爸直接認定為6即可。延續上一次的查詢,我們再多一項功能就是**再次遍歷**0的爸爸3、4,讓3和4的爸爸設定為6  ## 2. 基本並查集模板程式碼實現——第三版(優化) 程式碼實現也很簡單,我們只需要在find方法中加個四五行即可 ```java /** * @author 太白 */ public class UnionFind { private int[] arr; public UnionFind(int size) { arr = new int[size]; for (int i = 0; i < size; i++) { arr[i] = i; } } public int find(int son) { int father = arr[son]; while (father != arr[father]) { father = arr[father]; } // 直到迴圈到祖先為止 while (father != arr[son]) { // 儲存當前son的爸爸 // 因為要更改son的爸爸,所以要有個備份 int next = arr[son]; // 將son的爸爸改成father arr[son] = father; // 找到下一個爸爸(用備份的爸爸賦值給son即可) // 將son改成下一個爸爸,為下一個迴圈做準備 son = next; } return father; } public void union(int son1, int son2) { int father1 = find(son1); int father2 = find(son2); arr[father1] = father2; } } ``` 於是,我們的模板就算是做好了,我習慣在裡面新增兩個方法,一個是`isFamily(int, int)`,另一個是`getCategory()`,第一個可以檢測兩個人是不是同一個爸爸家族的成員,另外一個看看總共有多少個爸爸家族,這兩個方法經常在題目中用到,也很好實現,所以後續我們會結合例題,看如何十分簡單地運用該演算法解決一些相對複雜的題目。
# 四、例題 未完
