Python 3實現k-鄰近演算法以及 iris 資料集分類應用

阿新 • • 發佈：2019-01-09

前言

這個周基本在琢磨這個演算法以及自己利用Python3 實現自主程式設計實現該演算法。持續時間比較長，主要是Pyhton可能還不是很熟練，走了很多路，基本是一邊寫一邊學。不過，總算是基本搞出來了。不多說，進入正題。

1. K-鄰近演算法

1.1 基本原理

k近鄰法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一種基本分類與迴歸方法。它的工作原理是：存

在一個樣本資料集合，也稱作為訓練樣本集，並且樣本集中每個資料都存在標籤，即我們知道樣本集中每一個數據與所屬分

類的對應關係。輸入沒有標籤的新資料後，將新的資料的每個特徵與樣本集中資料對應的特徵進行比較，然後演算法提取樣本

最相似資料(最近鄰)的分類標籤。一般來說，我們只選擇樣本資料集中前k個最相似的資料，這就是k-近鄰演算法中k的出處，

通常k是不大於20的整數。最後，選擇k個最相似資料中出現次數最多的分類，作為新資料的分類。

1.2 一個例子

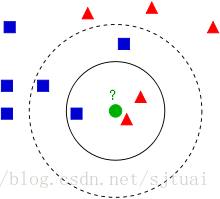
先來看一個圖：
這裡寫圖片描述

在這個圖裡面，我們可以看到有第三種顏色標記的標籤，藍色正方形，紅色三角形以及一個未知型別的綠色原點。那麼如何判斷這

個綠色點是屬於藍色家族的還是紅色家族的呢？

鄰近的思想就是計算這個綠色的點分別到它附近的點的距離，距離近就判定屬於這個型別，那麼K-鄰近就是讓待分類的這個點與所

有的已經分類點的距離，然後選取K個點，統計待分類的這個綠色點屬於哪個類別的數量比較多，就最終判定這個點屬於哪一個。

再回到圖，首先是K=3，可以看到實線裡面有兩個紅點，一個藍點，那麼判定這個綠傢伙屬於紅色的三角形型別。接著，選取了近

距離綠色點最近的5個點，這時，會發現，藍色系佔得更多，所以，判定這個綠傢伙是屬於藍色正方形的型別。

從這個例子可以看出來，K-鄰近的幾個基本關鍵點有：

點之間的距離計算
1. 歐式距離：
  d12=∑i=1n(x1i−x2i)−−−−−−−−−−−√
2. 曼哈頓距離：
  
  兩個向量a(x11,xx12,⋯,x1n)與b(x21,xx22,⋯,x2n)的曼哈頓距離為：
  
  d12=∑k=1n|x1k−x2k|
裡面有著更加詳細的關於距離的介紹。
距離排序
在這個計算的過程中，需要將最終的計算進行一個排序的。為下一步操作做好準備。
K的選擇
很明顯，對於這演算法，K的選取決定了整個演算法分類預測的準確性，可以說是其核心引數。從上面的例子也可以看出來，K=3和K=5得到的決然不同的結果的。

1.3 演算法步驟

（1）初始化距離
（2）計算待分類樣本和每個訓練集的距離
（3）排序
（4）選取K個最鄰近的資料
（5）計算K個訓練樣本的每類標籤出現的概率
（6）將待分類樣本歸為出現概率最大的標籤，分類結束。

2. Python實現K-鄰近演算法

2.1 K-鄰近函式

def mykNN(testData, trainData, label, K):

    # testData 待分類的資料集
    # trainData 已經分類好的資料集
    # label trainData資料集裡面的分類標籤
    # K是knn演算法中的K
    # testData=[101,20]
    # testData=np.array(testData)
    import numpy as np
    arraySize = trainData.shape
    trainingSampleNumber = arraySize[0]  # 樣本大小
    trainFeatureNumber = arraySize[1]  # 樣本特徵個數

    # 將待測試樣本拓展為和訓練集一樣大小矩陣
    testDataTemp = np.tile(testData, (trainingSampleNumber, 1))
    distanceMatrixTemp = (testDataTemp - trainData)**2
    distanceMatrix = np.sum(distanceMatrixTemp, axis=1)
    distanceMatrix = np.sqrt(distanceMatrix)
    # print('測試集與訓練集之間的歐式距離值為：\n')
    # print(distanceMatrix)
    # print()
    # np.argsort()得到矩陣排序後的對應的索引值
    sortedDistanceIndex = np.argsort(distanceMatrix)
    # print(sortedDistanceIndex)
    # 定義一個統計類別的字典
    labelClassCount = {}
    for i in range(K):
        labelTemp = label[sortedDistanceIndex[i]]  # 獲取排名前K的距離對應的類別值
        # print(labelTemp)
        labelClassCount[labelTemp] = labelClassCount.get(
            labelTemp, 0) + 1  # 統計前K中每個類別出現的次數

        # print(labelClassCount)

    sortedLabelClassCount = sorted(labelClassCount.items(), key=lambda item: item[
                                   1], reverse=True)  # 對字典進行降序排序
    # lambda item:item[1] 匿名函式，將利用dict.items()獲取的字典的key-value作為該匿名函式的變數輸入。# reverse=True 降序排列
    # print(sortedLabelClassCount)
    return sortedLabelClassCount[0][0]  # 返回最終的分類標籤值

2.2 牛刀小試-電影分類

舉個簡單的例子，我們可以使用k-近鄰演算法分類一個電影是愛情片還是動作片。

電影名稱	打鬥鏡頭	接吻鏡頭	電影型別
電影1	1	101	Romance
電影2	5	89	Romance
電影3	108	5	action
電影4	115	8	action

以上是已知的訓練樣本，我們需預測的是（101, 20）這個樣本，我們大致可以知道，打鬥鏡頭多則應該是動作片

資料集函式

def creatDataSet():
#定義資料集函式
    group = np.array([[1, 101, 5], [5, 89, 6], [108, 5, 100], [115, 8, 120]])
    label = ['romance Movie', 'romance Movie', 'action Movie', 'action Movie']
    # label=['r','r','a','a']
    return group, label
    # print(group)
    # print(label)'''

主函式

if __name__=='__main__':
#主函式
    finalIdentifyingResult=[]
    group,label=creatDataSet()
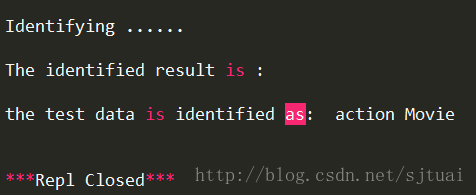
    print()
    print('Identifying ......')
    print()
    print('The identified result is :\n')


    testData=[101,20]
    testData=np.array(testData)
    finalIdentifyingLabel=mykNN(testData,group,label,3)
    print('the test data is identified as: ',finalIdentifyingLabel,'\n')

這裡寫圖片描述

可以看出來，分類結果和我們預測的是一致的，動作電影。

完整程式碼

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date    : 2017-08-28 16:04:25
# @Author  : AiYong ([email protected])
# @Link    : http://blog.csdn.net/sjtuai
# @Version : $Id$

import numpy as np

def creatDataSet():

    group = np.array([[1, 101], [5, 89], [108, 5], [115, 8]])
    label = ['romance Movie', 'romance Movie', 'action Movie', 'action Movie']
    return group, label
    print(group)
    print(label)

def mykNN(testData, trainData, label, K):

    arraySize = trainData.shape
    trainingSampleNumber = arraySize[0]
    testDataTemp = np.tile(testData, (trainingSampleNumber, 1))
    distanceMatrixTemp = (testDataTemp - trainData)**2
    distanceMatrix = np.sum(distanceMatrixTemp, axis=1)
    distanceMatrix = np.sqrt(distanceMatrix)
    sortedDistanceIndex = np.argsort(distanceMatrix)
    labelClassCount = {}
    for i in range(K):
        labelTemp = label[sortedDistanceIndex[i]]  
        labelClassCount[labelTemp] = labelClassCount.get(
            labelTemp, 0) + 1 
        sortedLabelClassCount = sorted(labelClassCount.items(), key=lambda item: item[
            1], reverse=True) 
        return sortedLabelClassCount[0][0] 

if __name__=='__main__':

    finalIdentifyingResult=[]
    group,label=creatDataSet()
    print()
    print('Identifying ......')
    print()
    print('The identified result is :\n')
    testData=[101,20]
    testData=np.array(testData)
    finalIdentifyingLabel=mykNN(testData,group,label,3)
    print('the test data is identified as: ',finalIdentifyingLabel,'\n')

2.3 考驗階段-鳶尾花資料集應用-分類預測

鳶尾花資料集

U can get description of ‘iris.csv’ at ‘http://aima.cs.berkeley.edu/data/iris.txt‘####
Definiation of COLs:
#1. sepal length in cm (花萼長) #
#2. sepal width in cm（花萼寬）#
#3. petal length in cm (花瓣長)
#4. petal width in cm（花瓣寬） #
#5. class: #
#– Iris Setosa #
#– Iris Versicolour #
#– Iris Virginica #
#Missing Attribute Values: None

資料集整理函式

def creatDataSet(fileName, test_size_ratio):
        # fileName is the data file whose type is string
        # test_size whose type is float is the ratio of test data in the whole
            # data set
    irisData = np.loadtxt(fileName, dtype=float,
                          delimiter=',', usecols=(0, 1, 2, 3))
    dataSize = irisData.shape
    irisLabel = np.loadtxt(fileName, dtype=str, delimiter=',', usecols=4)

    irisLabel = irisLabel.reshape(dataSize[0], 1)
    #這裡使用的一個函式是機器學習庫中的一個可以用來隨機選取訓練集和測試集的一個函式
    iristrainData, iristestData, iristrainDataLabel, iristestDataLabel = cross_validation.train_test_split(
        irisData, irisLabel, test_size=test_size_ratio, random_state=0)
    return iristrainData, iristestData, iristrainDataLabel, iristestDataLabel

矩陣轉化為列表函式

def ndarray2List(label):
    #這個函式的目的是為了後的資料服務的。
    label = label.tolist()
    finalLabel = []
    for i in range(label.__len__()):
        finalLabel.append('\n'.join(list(label[i])))
    return finalLabel

自定義混淆矩陣計算函式

def computingConfusionMatrix(trueResultA, modelPredictResultB):

        # trueResultA 正確的分類結果，numpy矩陣型別
        # modelPredictResultB 模型預測結果，numpy矩陣型別
        # labelType 分類標籤值，list列表型別
        #返回，confusionMatrix，混淆矩陣，numpy矩陣型別
        #返回，labelType，分類標籤，list列表型別
        #返回，Accuracy，分類爭取率，float浮點資料
    import numpy as np
    labelType = []
    for i in trueResultA:
        if i not in labelType:
            labelType.append(i)
    print(labelType)
    labelTypeNumber = labelType.__len__()
    confusionMatrix = np.zeros(
        [labelTypeNumber, labelTypeNumber], dtype='int64')
    finalCount = 0
    for i in range(labelTypeNumber):
        for j in range(trueResultA.__len__()):
            if modelPredictResultB[j] == labelType[i] and trueResultA[j] == labelType[i]:
                confusionMatrix[i][i] += 1
            else:
                for k in range(labelTypeNumber):
                    if k == i:
                        break
                    if modelPredictResultB[j] == labelType[k]:
                        confusionMatrix[i][k] += 1
                        break
    count = 0
    for i in range(labelTypeNumber - 1, -1, -1):
        if i == 0:
            break
        for j in range(labelTypeNumber - 1 - count):
            confusionMatrix[i][j] = confusionMatrix[
                i][j] - confusionMatrix[i - 1][j]
        count += 1
    totalTrueResult = 0
    for k in range(labelTypeNumber):
        totalTrueResult += confusionMatrix[k][k]
    Accuracy = float(totalTrueResult / modelPredictResultB.__len__()) * 100
    return confusionMatrix, labelType, Accuracy

定義圖裡面的橫縱座標軸標籤值的旋轉

def labelsRotation(labels, rotatingAngle):
    #labels 獲取的x，y軸的標籤值
    #rotatingAngle 想要旋轉的角度
    # 定義x，y軸標籤旋轉函式
    for t in labels:
        t.set_rotation(rotatingAngle)

定義混淆矩陣視覺化函式

def plotConfusionMatrix(confusionMatrix,labelType):
    import matplotlib.pyplot as plt
# 設定圖片的大小以及圖片解析度
    fig = plt.figure(figsize=(10, 8), dpi=120)
    plt.clf()
# 繪製圖，colormap是coolwarm
    plt.imshow(confusionMatrix, cmap=plt.cm.coolwarm, interpolation='nearest')
    plt.colorbar()
# 設定x，y的橫縱軸的標籤
    plt.xlabel('Predicted Result', fontsize=11)
    plt.ylabel('True Result', fontsize=11)
    cmSize = confusionMatrix.shape
    width = cmSize[0]
    height = cmSize[1]
    plt.xticks(fontsize=11)
    plt.yticks(fontsize=11)
# 設定橫縱座標的刻度標籤，顯示為分類標籤值
    x_locs, x_labels = plt.xticks(range(width), labelType[:width])
    y_locs, y_labels = plt.yticks(range(height), labelType[:height])
# 設定x，y軸的標籤是否旋轉
    labelsRotation(x_labels, 0)
    labelsRotation(y_labels, 0)

# 在圖裡面新增資料標籤
    confusionMatrix = confusionMatrix.T
    for x in range(width):  # 資料標籤
        for y in range(height):
            plt.annotate(confusionMatrix[x][y], xy=(
                x, y), horizontalalignment='center', verticalalignment='center')
    plt.grid(True, which='minor', linestyle='-')
# plt.rc('font',family='Times New Roman',size=15)
    font = {'family': 'monospace', 'weight': 'bold', 'size': 15}
    plt.rc('font', **font)
    plt.show()

主函式

if __name__ == '__main__':
    finalIdentifyingResult = []
    iriskNNResult = []
    iristrainData, iristestData, iristrainDataLabel, iristestDataLabel = creatDataSet(
        'iris.txt', 0.8)
    testGroup = iristestData
    trainGroup = iristrainData
    trainLabel = iristrainDataLabel

    testSize = testGroup.shape
    testSampleNumber = testSize[0]
    print()
    print('Identifying ......')
    print()
    print('The identified result is :\n')
    for i in range(testSampleNumber):
        testData = testGroup[i]
        finalIdentifyingLabel = mykNN(testData, trainGroup, trainLabel, 10)
        finalIdentifyingResult.append(finalIdentifyingLabel)
    iriskNNResult = np.array(
        finalIdentifyingResult).reshape(testSampleNumber, 1)
    print(finalIdentifyingResult)
    trueResultA = ndarray2List(iristestDataLabel)
    modelPredictResultB = finalIdentifyingResult
    confusionMatrix, labelType, Accuracy = computingConfusionMatrix(
        trueResultA, modelPredictResultB)
    print('The accuracy is :{a:5.3f}%'.format(a=Accuracy))
    plotConfusionMatrix(confusionMatrix, labelType)

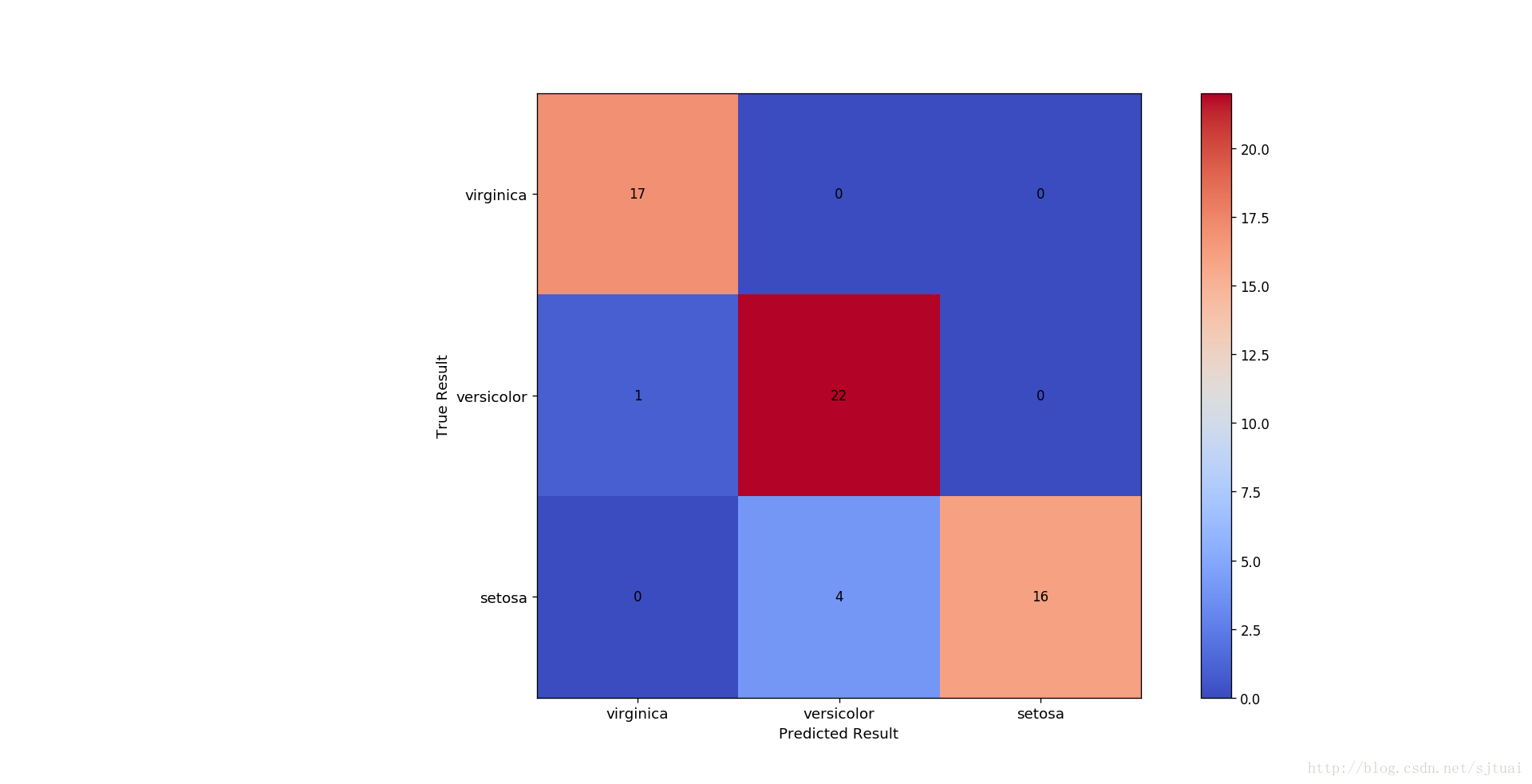
結果

這裡寫圖片描述

混淆矩陣
這裡寫圖片描述

從上面的結果可以看到這個準確率在90%以上，說明還是不錯的！

完整的程式結構

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date    : 2017-08-08 16:04:25
# @Author  : AiYong ([email protected])
# @Link    : http://blog.csdn.net/sjtuai
# @Version : $Id$

import numpy as np
from sklearn import cross_validation
import matplotlib.pyplot as plt


def mykNN(testData, trainData, label, K):

    # testData 待分類的資料集
    # trainData 已經分類好的資料集
    # label trainData資料集裡面的分類標籤
    # K是knn演算法中的K
    # testData=[101,20]
    # testData=np.array(testData)
    import numpy as np
    arraySize = trainData.shape
    trainingSampleNumber = arraySize[0]  # 樣本大小
    trainFeatureNumber = arraySize[1]  # 樣本特徵個數

    # 將待測試樣本拓展為和訓練集一樣大小矩陣
    testDataTemp = np.tile(testData, (trainingSampleNumber, 1))
    distanceMatrixTemp = (testDataTemp - trainData)**2
    distanceMatrix = np.sum(distanceMatrixTemp, axis=1)
    distanceMatrix = np.sqrt(distanceMatrix)
    # print('測試集與訓練集之間的歐式距離值為：\n')
    # print(distanceMatrix)
    # print()
    # np.argsort()得到矩陣排序後的對應的索引值
    sortedDistanceIndex = np.argsort(distanceMatrix)
    # print(sortedDistanceIndex)
    # 定義一個統計類別的字典
    labelClassCount = {}
    for i in range(K):
        labelTemp = label[sortedDistanceIndex[i]]  # 獲取排名前K的距離對應的類別值
        # print(labelTemp)
        labelClassCount[labelTemp] = labelClassCount.get(
            labelTemp, 0) + 1  # 統計前K中每個類別出現的次數

        # print(labelClassCount)

    sortedLabelClassCount = sorted(labelClassCount.items(), key=lambda item: item[
                                   1], reverse=True)  # 對字典進行降序排序
    # lambda item:item[1] 匿名函式，將利用dict.items()獲取的字典的key-value作為該匿名函式的變數輸入。# reverse=True 降序排列
    # print(sortedLabelClassCount)
    return sortedLabelClassCount[0][0]  # 返回最終的分類標籤值


def creatDataSet(fileName, test_size_ratio):
        # fileName is the data file whose type is string
        # test_size whose type is float is the ratio of test data in the whole
            # data set
    irisData = np.loadtxt(fileName, dtype=float,
                          delimiter=',', usecols=(0, 1, 2, 3))
    dataSize = irisData.shape
    irisLabel = np.loadtxt(fileName, dtype=str, delimiter=',', usecols=4)

    irisLabel = irisLabel.reshape(dataSize[0], 1)
    #這裡使用的一個函式是機器學習庫中的一個可以用來隨機選取訓練集和測試集的一個函式
    iristrainData, iristestData, iristrainDataLabel, iristestDataLabel = cross_validation.train_test_split(
        irisData, irisLabel, test_size=test_size_ratio, random_state=0)
    return iristrainData, iristestData, iristrainDataLabel, iristestDataLabel


def ndarray2List(label):
    #這個函式的目的是為了後的資料服務的。
    label = label.tolist()
    finalLabel = []
    for i in range(label.__len__()):
        finalLabel.append('\n'.join(list(label[i])))
    return finalLabel


def computingConfusionMatrix(trueResultA, modelPredictResultB):

        # trueResultA 正確的分類結果，numpy矩陣型別
        # modelPredictResultB 模型預測結果，numpy矩陣型別
        # labelType 分類標籤值，list列表型別
        #返回，confusionMatrix，混淆矩陣，numpy矩陣型別
        #返回，labelType，分類標籤，list列表型別
        #返回，Accuracy，分類爭取率，float浮點資料
    import numpy as np
    labelType = []
    for i in trueResultA:
        if i not in labelType:
            labelType.append(i)
    print(labelType)
    labelTypeNumber = labelType.__len__()
    confusionMatrix = np.zeros(
        [labelTypeNumber, labelTypeNumber], dtype='int64')
    finalCount = 0
    for i in range(labelTypeNumber):
        for j in range(trueResultA.__len__()):
            if modelPredictResultB[j] == labelType[i] and trueResultA[j] == labelType[i]:
                confusionMatrix[i][i] += 1
            else:
                for k in range(labelTypeNumber):
                    if k == i:
                        break
                    if modelPredictResultB[j] == labelType[k]:
                        confusionMatrix[i][k] += 1
                        break
    count = 0
    for i in range(labelTypeNumber - 1, -1, -1):
        if i == 0:
            break
        for j in range(labelTypeNumber - 1 - count):
            confusionMatrix[i][j] = confusionMatrix[
                i][j] - confusionMatrix[i - 1][j]
        count += 1
    totalTrueResult = 0
    for k in range(labelTypeNumber):
        totalTrueResult += confusionMatrix[k][k]
    Accuracy = float(totalTrueResult / modelPredictResultB.__len__()) * 100
    return confusionMatrix, labelType, Accuracy
    def labelsRotation(labels, rotatingAngle):
        #labels 獲取的x，y軸的標籤值
        #rotatingAngle 想要旋轉的角度
        # 定義x，y軸標籤旋轉函式
        for t in labels:
            t.set_rotation(rotatingAngle)


def plotConfusionMatrix(confusionMatrix,labelType):
    import matplotlib.pyplot as plt
    fig = plt.figure(figsize=(10, 8), dpi=120)
    plt.clf()
    plt.imshow(confusionMatrix, cmap=plt.cm.coolwarm, interpolation='nearest')
    plt.colorbar()
    plt.xlabel('Predicted Result', fontsize=11)
    plt.ylabel('True Result', fontsize=11)
    cmSize = confusionMatrix.shape
    width = cmSize[0]
    height = cmSize[1]
    plt.xticks(fontsize=11)
    plt.yticks(fontsize=11)
    x_locs, x_labels = plt.xticks(range(width), labelType[:width])
    y_locs, y_labels = plt.yticks(range(height), labelType[:height])
    labelsRotation(x_labels, 0)
    labelsRotation(y_labels, 0)
    confusionMatrix = confusionMatrix.T
    for x in range(width):  # 資料標籤
        for y in range(height):
            plt.annotate(confusionMatrix[x][y], xy=(
                x, y), horizontalalignment='center', verticalalignment='center')
    plt.grid(True, which='minor', linestyle='-')
    font = {'family': 'monospace', 'weight': 'bold', 'size': 15}
    plt.rc('font', **font)
    plt.show()


if __name__ == '__main__':
    finalIdentifyingResult = []
    iriskNNResult = []
    iristrainData, iristestData, iristrainDataLabel, iristestDataLabel = creatDataSet(
        'iris.txt', 0.8)
    testGroup = iristestData
    trainGroup = iristrainData
    trainLabel = iristrainDataLabel

    testSize = testGroup.shape
    testSampleNumber = testSize[0]
    print()
    print('Identifying ......')
    print()
    print('The identified result is :\n')
    for i in range(testSampleNumber):
        testData = testGroup[i]
        finalIdentifyingLabel = mykNN(testData, trainGroup, trainLabel, 10)
        finalIdentifyingResult.append(finalIdentifyingLabel)
    iriskNNResult = np.array(
        finalIdentifyingResult).reshape(testSampleNumber, 1)
    print(finalIdentifyingResult)
    trueResultA = ndarray2List(iristestDataLabel)
    modelPredictResultB = finalIdentifyingResult
    confusionMatrix, labelType, Accuracy = computingConfusionMatrix(
        trueResultA, modelPredictResultB)
    print('The accuracy is :{a:5.3f}%'.format(a=Accuracy))
    plotConfusionMatrix(confusionMatrix, labelType)

3. 總結

這裡有非常好的關於K-鄰近分類的理論以及一些比較好的圖理：

3.1 優缺點

優點

簡單，易於理解，易於實現，無需估計引數，無需訓練
適合對稀有事件進行分類（例如當流失率很低時，比如低於0.5%，構造流失預測模型）
特別適合於多分類問題(multi-modal,物件具有多個類別標籤)，例如根據基因特徵來判斷其功能分類，kNN比SVM的表現要好

缺點

懶惰演算法，對測試樣本分類時的計算量大，記憶體開銷大，評分慢
可解釋性較差，無法給出決策樹那樣的規則。

3.2 一些問題集錦

1、k值設定為多大？
k太小，分類結果易受噪聲點影響；k太大，近鄰中又可能包含太多的其它類別的點。（對距離加權，可以降低k值設定的影響）
k值通常是採用交叉檢驗來確定（以k=1為基準）
經驗規則：k一般低於訓練樣本數的平方根

2、類別如何判定最合適？
投票法沒有考慮近鄰的距離的遠近，距離更近的近鄰也許更應該決定最終的分類，所以加權投票法更恰當一些。

3、如何選擇合適的距離衡量？

高維度對距離衡量的影響：眾所周知當變數數越多，歐式距離的區分能力就越差。
變數值域對距離的影響：值域越大的變數常常會在距離計算中佔據主導作用，因此應先對變數進行標準化。

4、訓練樣本是否要一視同仁？

在訓練集中，有些樣本可能是更值得依賴的。
可以給不同的樣本施加不同的權重，加強依賴樣本的權重，降低不可信賴樣本的影響。

5、效能問題？

kNN是一種懶惰演算法，平時不好好學習，考試（對測試樣本分類）時才臨陣磨槍（臨時去找k個近鄰）。
懶惰的後果：構造模型很簡單，但在對測試樣本分類地的系統開銷大，因為要掃描全部訓練樣本並計算距離。

Python 3實現k-鄰近演算法以及 iris 資料集分類應用

前言

1. K-鄰近演算法

1.1 基本原理

1.2 一個例子

1.3 演算法步驟

2. Python實現K-鄰近演算法

2.1 K-鄰近函式

2.2 牛刀小試-電影分類

2.3 考驗階段-鳶尾花資料集應用-分類預測

3. 總結

3.1 優缺點

3.2 一些問題集錦

參考連結：

Python 3實現k-鄰近演算法以及 iris 資料集分類應用

python3實現K-鄰近演算法(機器學習實戰中程式碼)

機器學習演算法及程式碼實現--K鄰近演算法

Python中的k—近鄰演算法（處理常見的分類問題）

基於 K-Means 對 IRIS 資料集分類

機器學習入門實戰——感知機演算法實戰Iris資料集

利用 sklearn SVM 分類器對 IRIS 資料集分類

基於決策樹模型對 IRIS 資料集分類

用python實現K均值演算法

python實現k近鄰演算法

Inception服務的安裝以及使用Python 3 實現MySQL的審計

Python實現K近鄰演算法_分類器

Python實現k-means演算法

python 機器學習K-means演算法實現

java實現k-means演算法（用的鳶尾花iris的資料集，從mysq資料庫中讀取資料）

Python實現k-近鄰演算法

機器學習實戰讀書筆記(1)--k鄰近演算法

機器學習實戰（Machine Learning in Action）學習筆記————02.k-鄰近演算法（KNN）

Python 3 實現數字轉換成Excel列名（10進位制到26進位制的轉換函式）

Python 3 實現插入排序

Python 3實現k-鄰近演算法以及 iris 資料集分類應用

前言

1. K-鄰近演算法

1.1 基本原理

1.2 一個例子

1.3 演算法步驟

2. Python實現K-鄰近演算法

2.1 K-鄰近函式

2.2 牛刀小試-電影分類

2.3 考驗階段-鳶尾花資料集應用-分類預測

3. 總結

3.1 優缺點

3.2 一些問題集錦

參考連結：

相關推薦