淺談微積分以及泰勒展開 # 前言 > **~~這年頭不會微積分幹什麼都不行啊~~** # 一.微積分 > 微積分其實就只有兩種運算，一種是**求導**，另一種是求**不定積分**。並且其為**互逆運算** ## 導數 ### 導數的定義 > 導數（Derivative），也叫導函式值。又名[微商](https://baike.baidu.com/item/微商/11036713)，是[微積分](https://baike.baidu.com/item/微積分/6065)中的重要基礎概念。當函式y=f(x)的[自變數](https://baike.baidu.com/item/自變數/6895256)x在一點x0上產生一個增量Δx時，函式輸出值的增量Δy與自變數增量Δx的比值在Δx趨於0時的[極限](https://baike.baidu.com/item/極限/3564509)a如果存在，a即為在x0處的導數，記作f'(x0)或df(x0)/dx。——百度百科 * 簡而言之，所謂導數所反映的就是一個函式的變化趨勢，其同樣是一個函式。設 $f'(x)$ 為 $f(x)$ 的導數，那麼 $f'(x_0)$ 就是 $f(x)$ 的影象上過橫座標為 $x_0$ 的點的切線的斜率。 * 講的更容易理解一點，我們先拋開所有關於微積分的什麼極限啊什麼的。僅僅考慮一個問題：什麼是變化率？ * 你可能會說：“變化率就是 $\Delta y$ 和 $\Delta x$ 的比值。”確實，就是這樣。它反映的是一個變化的趨勢，就是隨著橫座標 $x$ 的變化，縱座標 $y$ 變化了多少。如果變化率越大，那麼相應的，$y$ 的變化就會越大。 * 而導數的本質就是變化率，只不過將其放在了一個十分微小的範圍內。可以近似地看成影象在某個點的變化率。 * 那麼這裡有一個關於導數的悖論：“一個函式的導數所反映的是該函式在每個點時的變化率。”但一個點談何變化？它連 $\Delta x$ 和 $\Delta y$ 都沒有。 * 所以，不要把這當做導數的定義，**別把導數看成某一點瞬時的變化率，而是看成某一點附近的變化率的最佳近似。** ### 導數的求法 #### 普通函式 * 這個很簡單，按照定義來就行了。 * 我們假設一個函式在 $x_0$ 處產生了一個非常小的增量 $dx$ ，同時導致了縱座標的增量 $df$ ，那麼根據定義，其導數即為 $\frac{df}{dx}$ 。 * 以 $f(x)=x^2$ 為例： $$ \begin{aligned} \frac{df}{dx} &=\frac{f(x_0+dx)-f(x_0)}{dx}\\ &=\frac{x_0^2+2dx\cdot x+dx^2-x_0^2}{dx}\\ &=2x+dx \end{aligned}\\ f'(x)=\lim_{dx\rightarrow 0} \frac{df}{dx}=\lim_{dx\rightarrow 0} 2x+dx=2x $$ 當 $dx$ 無限趨近於 $0$ 時，我們可以將其省略，那麼 $\frac{df}{dx}=2x$ 。所以函式 $f(x)=x^2$ 的導數為 $f'(x)=2x$ 。 * 但是，有沒有更直觀的方法呢？我可不想每次求導數的時候都去這樣推一遍。自然是有的。用幾何法也可以證明。 * 讓我們假設現在有一個邊長為 $x$ 的正方形，那麼它的面積就為 $x^2$ ，該函式的函式值。此時如果該正方形的邊長增加一個很小的量 $dx$ ，那麼它的面積 $ds$ 就會增加 $dx\cdot x+dx\cdot +dx^2$ ，因為 $dx$ 本身就是一個極小的值，那麼其平方會變得更小，我們可以直接忽略不計。那麼 $\frac{ds}{dx}$ 的值就為 $2x$ ，與我們用代數法算出來的答案是一樣的。 * ~~假如我們學過微積分~~，這時我們就會發現，導數裡面的係數 $2$ 居然和原函式的指數 $2$ 相同！這是巧合嗎？~~顯然不是~~。我們試著寫出函式 $f(x)=x^3$ 的導數 $f'(x)=3x^2$，發現居然和二次函式一樣。那是不是…… * 好吧我坦白，這就是冪函式的共性……除此之外，還有許多其他類的函式也具有相同的性質： 1. $C'=0$ （$C$ 為任意常數） 2. $(x^a)'=ax^{a-1}$ 3. $(e^x)'=e^x$ 4. $(\ln\:x)'=\frac{1}{x}$ * 我們發現這個裡面有一個非常神奇的函式 $e^x$ ，它的導數居然是它自己。怎麼說呢，其實自然常數 $e$ 就是這樣定義的。我們對任意指數函式求導，以 $2^x$ 為例： $$ (2^x)'=\frac{2^{x+dx}-2^x}{dx}=\frac{2^x\cdot 2^{dx}-2^x}{dx}=2^x\cdot \frac{2^{dx}-1}{dx} $$ 當 $dx$ 趨近於 $0$ 的時候，$\frac{2^{dx}-1}{dx}$ 會趨近於某個常數。也就是說，$2^x$ 的導數是它自己乘上一個固定的常數。說到這裡你可能就明白了，自然常數 $e$ 的值即為 $\lim_{dx\rightarrow 0}\frac{e^{dx}-1}{dx}=1\Rightarrow e=\lim_{dx\rightarrow 0}(dx+1)^{\frac{1}{dx}}$ 再多說一點，其實 $2^x$ 的導數的那個常數就是 $\ln\:(2)$ 。為什麼？看完複合函式的求導就知道了。 #### 非普通函式 > 普通函式適用的範圍畢竟還是太小了，生活中大多數函式都為非普通函式，還是要掌握其求導方法。 * 非普通函式的求導滿足一下三個規則： 1. 和規則：$\begin{aligned}\left(f(x)+g(x)\right)'&=f'(x)+g'(x)\\ \left(af(x)\right)'&=af'(x)\end{aligned}$ 2. 積規則：$\left(f(x)\cdot g(x)\right)'=f'(x)g(x)+f(x)g'(x)$ （左乘右導，右乘左導） 3. 鏈規則：$\left(f\left(g(x)\right)\right)'=g'(x)f'\left(g(x)\right)$ * 這三種規則都有其直觀的幾何理解，就比如積規則，可以想象一個分別以兩個函式的函式值為邊長的長方形，看其面積隨著邊長怎樣變化。鏈規則則可想象三根數軸，各個因變數是如何隨著各自的自變數的變化而變化。 * 類似的方法還有很多，就不再贅述了。 * 講一講之前的那個指數函式求導的常數證明吧： $$ (2^x)'=\left(e^{\ln(2)x}\right)'=\ln(2)\left(e^{\ln(2)}\right)^x=\ln(2)\cdot2^x $$ ### 高階導數 * 我們把一個函式導數的導數稱作二階導數，其所反映的是該函式的導數的變化量，即變化量的變化量。 * 三階導數以及更高階的導數以此類推。 * 舉個栗子：速度是路程的導數，而加速度是速度的導數，所以加速度是路程的二階導數。 * 所以對於冪函式來說，其不斷求導的過程就是不斷地降冪 ，並且係數會以連乘 $\prod$ 的形式存在。因為每一次求導，都會將係數乘以當前的指數，並且指數減一。 * $For\:instance:f(x)=x^{10}\Rightarrow f^{(5)}(x)=\left(\prod_{i=6}^{10}i\right)x^5$ ## 積分 ### 積分的定義 > **積分**是[微積分](https://baike.baidu.com/item/微積分)學與[數學分析](https://baike.baidu.com/item/數學分析/3123)裡的一個核心概念。通常分為**[定積分](https://baike.baidu.com/item/定積分/7128801)**和**[不定積分](https://baike.baidu.com/item/不定積分/6082893)**兩種。直觀地說，對於一個給定的正實值函式，在一個實數[區間](https://baike.baidu.com/item/區間/1273117)上的定積分可以理解為在座標平面上，由曲線、直線以及軸圍成的[曲邊梯形](https://baike.baidu.com/item/曲邊梯形/10483836)的面積值（一種確定的**[實數](https://baike.baidu.com/item/實數/296419)**值）。——百度百科 * 對於積分來說，就理解成面積就好了。 * 積分分為定積分和不定積分兩種。定積分為一個確定的數值，而不定積分則是一個函式。 * 求不定積分和求導數互為逆運算。為什麼？我們假設 $f(x)$ 圍成的面積的函式為 $g(x)$ ，橫座標增加 $dx$ ，那麼面積的增加量 $ds$ 可以近似地看做一個長方形，那麼 $g'(x)=\frac{ds}{dx}$，就是當前長方形的高，恰好就是 $f(x)$ 的函式值。 ### 積分的求法 * 很簡單，因為求不定積分和求導數是一對互逆運算，那麼我們就可以根據已知的導數反推出原函式。 * 如上面的幾個導數求不定積分： 1. $\int 0dx=C$ 2. $\int x^adx=\frac{1}{a+1}x^{a+1}+C$ 3. $\int e^xdx=e^x+C$ 4. $\int x^{-1}dx=\ln x+C$ # 二.泰勒級數 > 在數學中，泰勒級數（英語：Taylor series）用無限項連加式——[級數](https://baike.baidu.com/item/級數/2381414)來表示一個函式，這些相加的項由函式在某一點的[導數](https://baike.baidu.com/item/導數/579188)求得。——百度百科 * 說白了，泰勒級數就是用一個多項式去模擬一個函式，至少在 $OI$ 中是這樣的，可以用於牛頓迭代的推導以及生成函式的變形。 * 我們將多項式看做一個函式，那麼問題就變成了如何用一個函式去模擬另外一個函式。 * 我們先從 $x=0$ 下手~~（因為簡單）~~ * 如果兩個函式影象一樣的話，那麼至少在 $x=0$ 時的函式值要相等吧，所以我們讓其的常數項相等。 * 如果兩個函式影象一樣的話，那麼至少在$x=0$ 附近的變化趨勢要相等吧，所以我們讓其導數相等。 * 如果兩個函式影象一樣的話，那麼至少在$x=0$ 附近的變化趨勢的變化趨勢要相等吧，所以我們讓其二階導數相等。 * …… * 可以證明，在 $x=0$ 時，$g(x)$ 的 $n$ 階導數只與 $x^n$ 的係數有關係，因為之前的求導時已經變成 $0$ ，而後邊的因為含有 $x$ 而為 $0$ * 那麼在 $x=0$ 時我們就得到了函式 $f(x)$ 的近似擬合函式 $$ g(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\ldots+\frac{f^{(n)}(0)}{n!}x^n $$ * 這個叫做麥克勞林級數。 * 等等，那泰勒去哪兒了？ * 剛剛所展現的是在 $x=0$ 附近擬合的過程。只需稍作替換，就可以在任意地方 $x=x_0$ 處擬合了。這就是泰勒級數： $$ g(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\ldots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n $$ * 所以麥克勞林級數只是泰勒級數在 $x=0$ 的特殊情況。 * 下面是我在 $Geogebra$ 上所擬合的 $\cos(x)$ 以及 $e^x$ 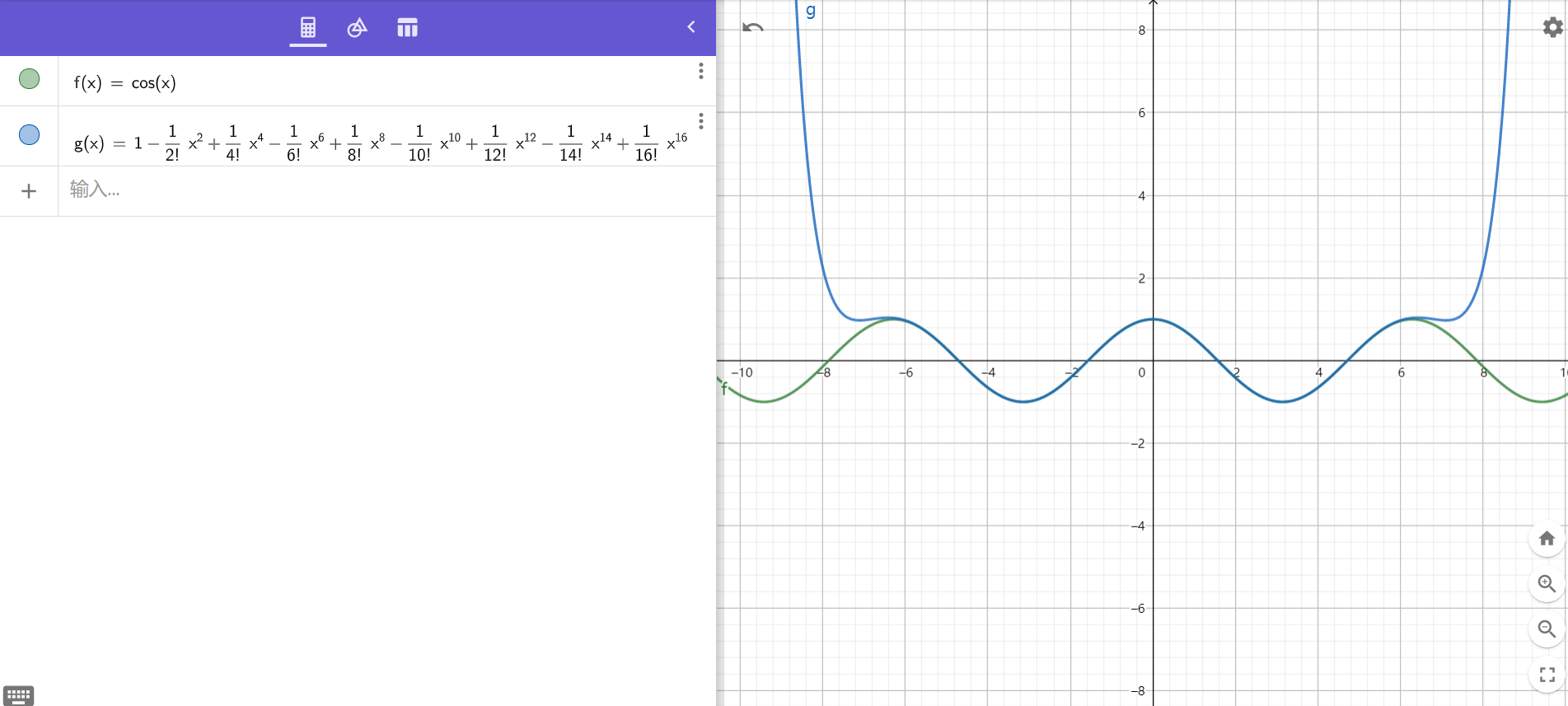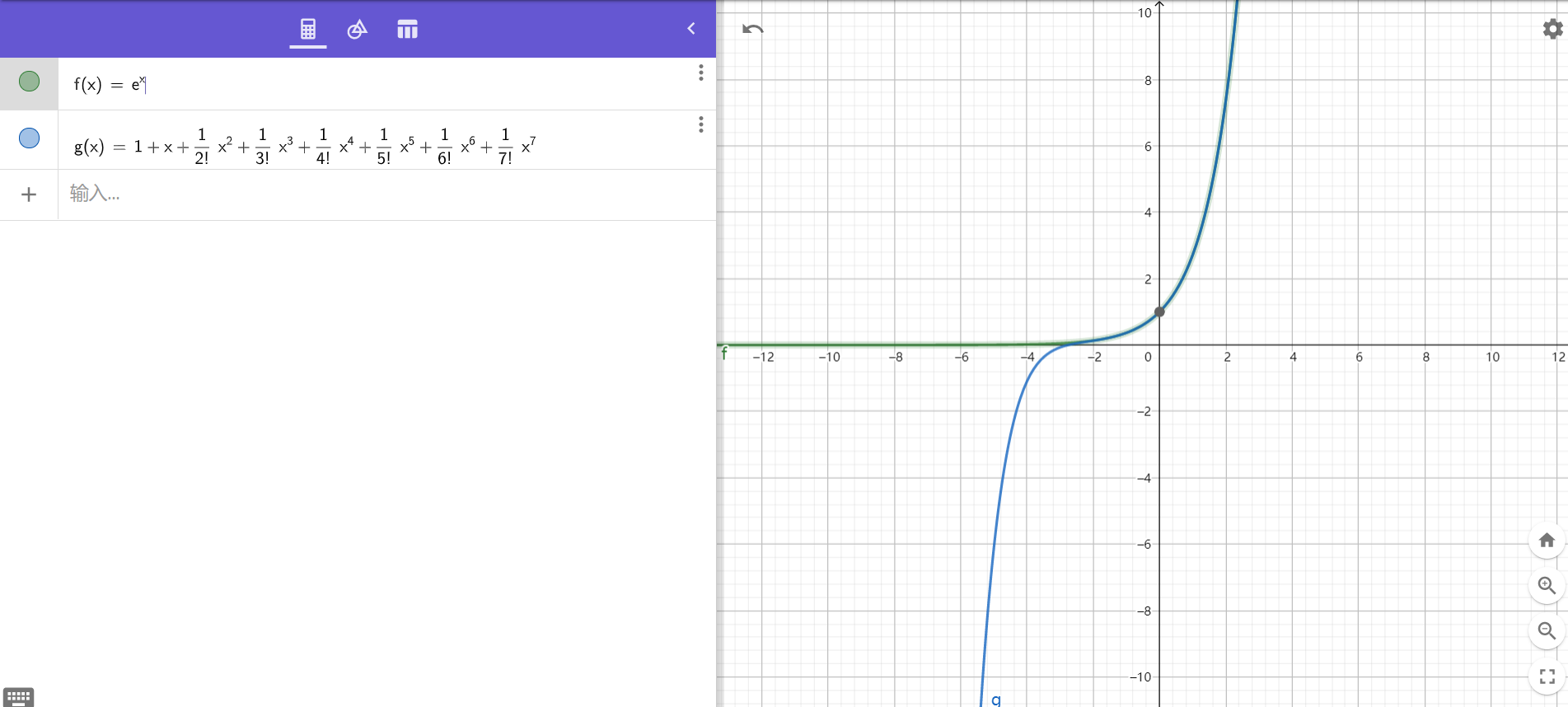：  * **數學真的是一門美妙的學科。** # 一些有趣的東西 * 為什麼圓的面積公式為 $\pi r^2$ ？我們可以嘗試將圓分成許許多多的圓環，並且將其展平，近似地看做一個個長方形。然後將他們由小到大放在座標軸上。當相差的半徑足夠小的時候，就可以看作是一個底為 $r$ （半徑），高為 $2\pi r$ （周長）的三角形，故得圓的面積公式。 * 為什麼三角形鄰邊比上斜邊叫做餘弦？因為餘弦函式是正弦函式的導數。即 $$ \begin{aligned} \sin'(x)&=\cos(x)\\ \cos'(x)&=-\sin(x)\\ \left(-\sin(x)\right)'&=-\cos(x)\\ \left(-\cos(x)\right)'&=\sin(x) \end{aligned} $$

——2021年2月8日