數理統計10(習題篇):尋找UMVUE
阿新 • • 發佈:2021-02-11
利用L-S定理,充分完備統計量法是尋找UMVUE的最方便方法,不過實際運用時還需要一些小技巧,比如如何寫出充分完備統計量、如何找到無偏估計、如何求條件期望,等等。課本上的例題幾乎涵蓋了所有這些技巧,我們今天以一些課後習題為例,解析這些技巧的實際運用。由於本系列為我獨自完成的,缺少審閱,**如果有任何錯誤,歡迎在評論區中指出,謝謝**!
[Toc]
## Part 1:尋找充分統計量
不論是使用什麼方法,UMVUE首先必須是充分統計量的函式,因此找到充分統計量是必要的,如果是指數族,充分統計量還就是完備統計量。單總體情況下,運用因子分解定理尋找充分統計量已經不陌生,這裡給出一個雙總體情況下的例子。
**第一題(34)**:設$X_1,\cdots,X_m\stackrel{\text{i.i.d.}}\sim N(\mu,\sigma^2)$,$Y_1,\cdots,Y_n\stackrel{\text{i.i.d.}}\sim N(\mu,2\sigma^2)$,且兩組樣本相互獨立。試求$\mu,\sigma^2$的充分統計量。
要求充分統計量,其步驟一定是寫出**概率函式**,在這裡就是樣本聯合密度函式。由於兩組樣本相互獨立,即每一個樣本之間都是相互獨立的,所以聯合密度函式就是每一個密度相乘。以下,我們用$\bar X,\bar Y$代表兩組樣本的樣本均值,$S^2_x,S^2_y$代表兩組樣本的樣本方差,另外,離差平方和會是常用於正態分佈的量,因此引入它們。
$$
Q^2_x=(m-1)S_x^2=\sum_{j=1}^m(X_j-\bar X)^2,\\
Q_y^2=(n-1)S_y^2=\sum_{j=1}^n(Y_j-\bar Y)^2.
$$
現在來寫出樣本聯合密度函式。
$$
\begin{aligned}
f(\boldsymbol{x},\boldsymbol{y})&=\left(\frac{1}{\sqrt{2\pi\sigma^2}} \right)^{m}\left(\frac{1}{\sqrt{4\pi\sigma^2}} \right)^n\exp\left\{-\frac{\sum_{j=1}^m(x_j-\mu)^2}{2\sigma^2}-\frac{\sum_{j=1}^n(y_j-\mu)^2}{4\sigma^2} \right\}\\
&=\frac{C}{\sigma^{m+n}}\exp\left\{-\frac{2\sum_{j=1}^mx_j^2+\sum_{j=1}^n y_j^2}{4\sigma^2}+\frac{\mu(2m\bar x+n\bar y)}{2\sigma^2}-\frac{\mu^2(2m+n)}{4\sigma^2} \right\} \\
&=\frac{Ce^{-\frac{\mu^2(2m+n)}{4\sigma^2}}}{\sigma^{m+n}}\exp\left\{ -\frac{1}{4\sigma^2}\left(2\sum_{j=1}^mx_j^2+\sum_{j=1}^ny_j^2 \right)+\frac{\mu}{2\sigma^2}(2m\bar x+n\bar y) \right\}.
\end{aligned}
$$
令
$$
\theta_1=-\frac{1}{4\sigma^2},\quad \theta_2=\frac{\mu}{2\sigma^2},
$$
則
$$
T_1=2\sum_{j=1}^mX_j^2+\sum_{j=1}^nY_j^2,\quad T_2=2m\bar X+n\bar Y
$$
是$(\theta_1,\theta_2)$的充分完全統計量,接下來對它們做無偏修正得到UMVUE。由於對正態分佈$Z\sim N(\mu,\sigma^2)$而言,$\mathbb{E}(Z^2)=\mu^2+\sigma^2$,所以
$$
\mathbb{E}(T_1)=2m(\mu^2+\sigma^2)+n(\mu^2+2\sigma^2)=(2m+n)\mu^2+2(m+n)\sigma^2,\\
\mathbb{E}(T_2)=(2m+n)\mu,\\
\mathbb{E}(T_2^2)=4m^2\mathbb{E}(\bar X^2)+n^2\mathbb{E}(\bar Y^2)+4mn\mathbb{E}(\bar X\bar Y)=(2m+n)^2\mu^2+2(2m+n)\sigma^2,\\
\mathbb{E}[T_2^2-(2m+n)T_1]=2(2m+n)(1-m-n)\sigma^2
$$
因此$\mu,\sigma^2$的UMVUE是
$$
\hat\mu=\frac{2m\bar X+n\bar Y}{2m+n},\quad \hat\sigma^2=\frac{T_2^2-(2m+n)T_1}{2(2m+n)(1-m-n)}.
$$
> 取$\mu=5,\sigma=2$進行模擬。當$m=5,n=6$時,估計量的示意圖為:
>
> 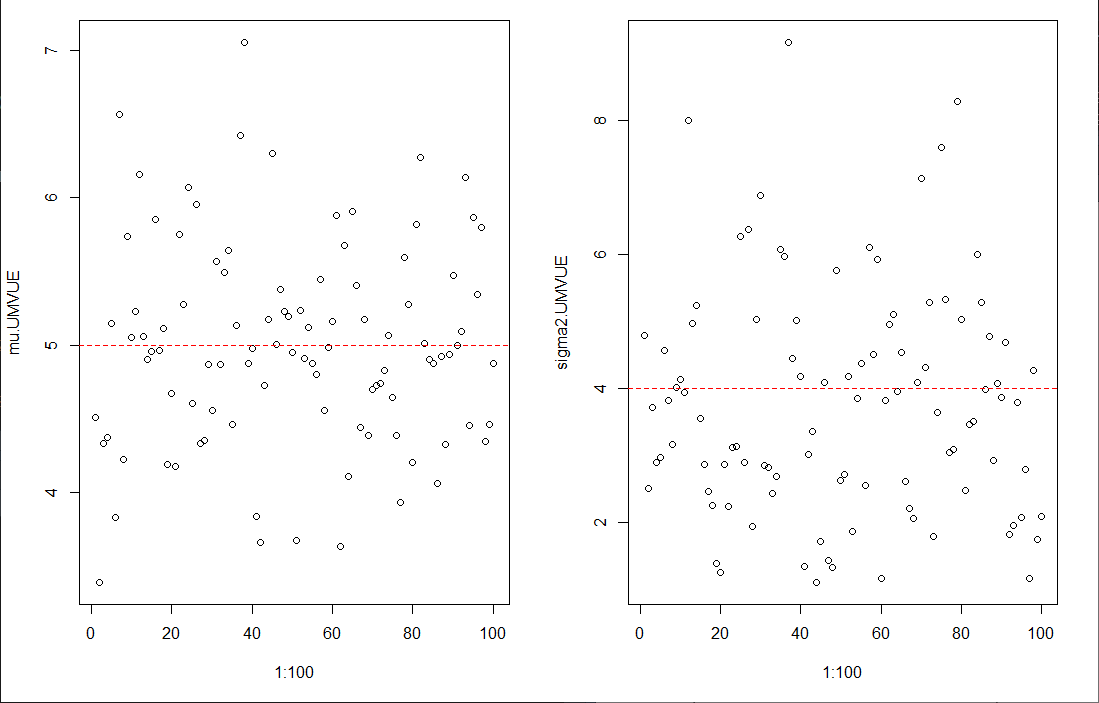 >
> 當$m=100,n=200$時,估計量示意圖為
>
>
>
> 當$m=100,n=200$時,估計量示意圖為
>
> 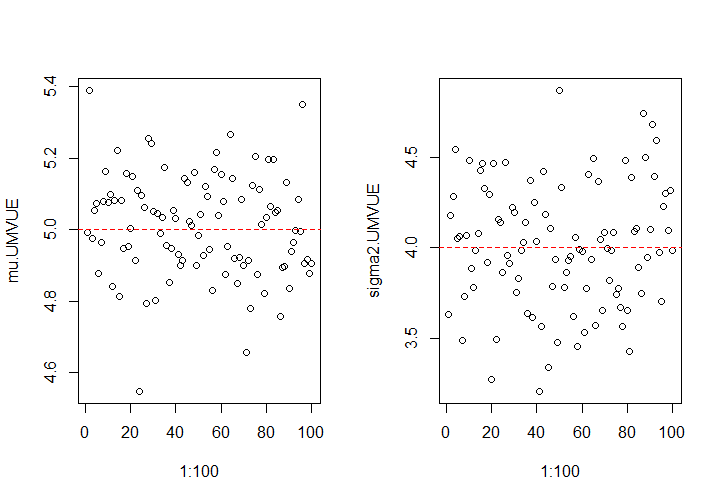 >
> 繪製在一張圖上:
>
>
>
> 繪製在一張圖上:
>
> 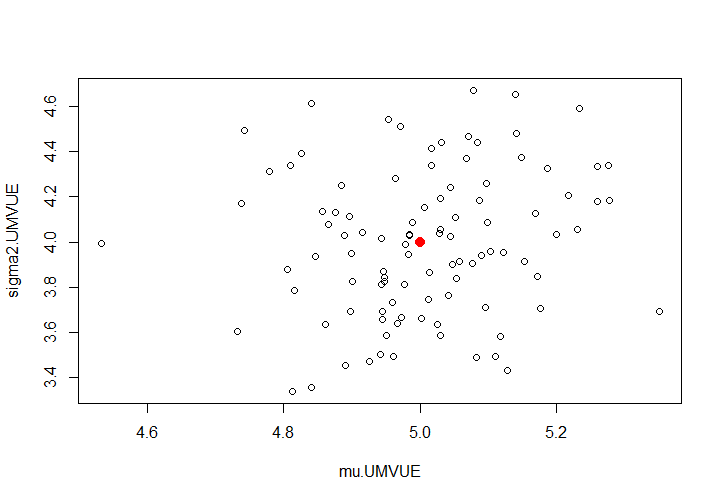 >
> 程式碼見附錄。
## Part 2:無偏修正
由於尋找充分完備統計量的過程比較機械,許多時候難點並不在此,而是在於將充分完備統計量進行一定的變換,得到充分完備統計量的無偏函式估計。其關鍵,就在於將充分完備統計量進行一定的次數變換,達到待估引數所需的次數。
**第二題(31)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim N(0,\sigma^2)$,求$\sigma$和$\sigma^4$的UMVUE。
均值已知,容易求得$\sigma^2$的充分完備統計量就是
$$
T=\sum_{j=1}^n X_j^2.
$$
關鍵在於找到合適的$h(\cdot)$,使得$\mathbb{E}(h(T))=\sigma$,或者$\mathbb{E}(h(T))=\sigma^4$。顯然,我們會從$\sqrt{T}$和$T^2$上入手,因此,我們需要先給出$T$的密度,才能求其函式的期望。容易發現
$$
\frac{T}{\sigma^2}=\sum_{j=1}^n\left(\frac{X_j}{\sigma} \right)^2\sim \chi^2(n)\Rightarrow T\sim \Gamma\left(\frac{n}{2},\frac{1}{2\sigma^2} \right),
$$
所以$T$的密度函式是
$$
p(t)=\frac{I_{t>
>
> 程式碼見附錄。
## Part 2:無偏修正
由於尋找充分完備統計量的過程比較機械,許多時候難點並不在此,而是在於將充分完備統計量進行一定的變換,得到充分完備統計量的無偏函式估計。其關鍵,就在於將充分完備統計量進行一定的次數變換,達到待估引數所需的次數。
**第二題(31)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim N(0,\sigma^2)$,求$\sigma$和$\sigma^4$的UMVUE。
均值已知,容易求得$\sigma^2$的充分完備統計量就是
$$
T=\sum_{j=1}^n X_j^2.
$$
關鍵在於找到合適的$h(\cdot)$,使得$\mathbb{E}(h(T))=\sigma$,或者$\mathbb{E}(h(T))=\sigma^4$。顯然,我們會從$\sqrt{T}$和$T^2$上入手,因此,我們需要先給出$T$的密度,才能求其函式的期望。容易發現
$$
\frac{T}{\sigma^2}=\sum_{j=1}^n\left(\frac{X_j}{\sigma} \right)^2\sim \chi^2(n)\Rightarrow T\sim \Gamma\left(\frac{n}{2},\frac{1}{2\sigma^2} \right),
$$
所以$T$的密度函式是
$$
p(t)=\frac{I_{t> 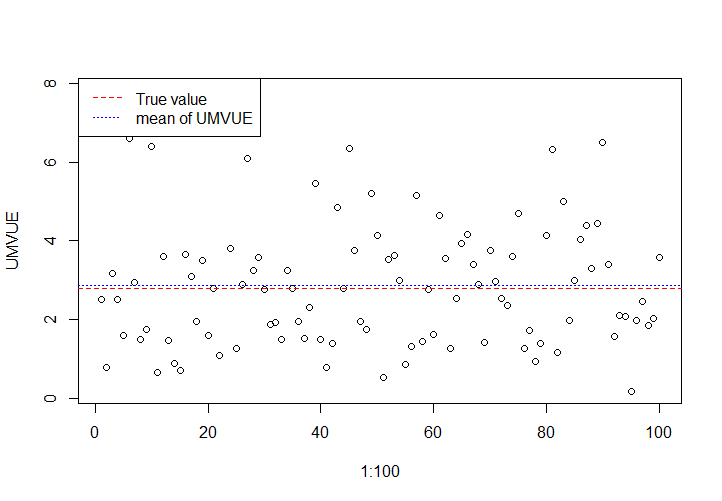 ## Part 3:待定係數
有時候,無偏估計不是通過簡單的升次就能找到的,為了求出符合題意的$h(\cdot)$,可以使用待定係數法。待定係數法假定$h(\cdot)\in\mathcal P(\mathbb{R})$是一個多項式,從而根據次數關係確定$h(\cdot)$的各項係數,即使待估引數不是顯然的多項式,也可以通過泰勒展開變成多項式的形式(但一般很少這麼做)。
**第四題(33)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim B(1,p)$,求$p^s$的UMVUE和$p^s+(1-p)^{n-s}$的UMVUE。
容易驗證$p$的UMVUE是$T=\sum_{j=1}^nX_j\sim B(n,p)$,假定$h(T)$是$p^s$的UMVUE,則有
$$
\mathbb{E}[h(T)]=\sum_{j=0}^nh(j)C_{n}^j p^j(1-p)^{n-j}=p^s.
$$
左邊部分略顯繁瑣,對其進行整理,得到
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p}\right)^j(1-p)^n=p^s,
$$
所以
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p} \right)^j=\frac{p^s}{(1-p)^n}=\left(\frac{p}{1-p} \right)^s\left(\frac{1}{1-p} \right)^{n-s}.
$$
這裡要運用一個**二項分佈的常用換元**:
$$
R=\frac{p}{1-p}\Rightarrow p=\frac{R}{R+1},1-p=\frac{1}{R+1}.
$$
將等式兩邊變成
$$
\sum_{j=0}^n h(j)C_n^jR^j=R^s(1+R)^{n-s}=\sum_{k=0}^{n-s}C_{n-s}^kR^{s+k}=\sum_{k=s}^{n}C_{n-s}^{k-s}R^k.
$$
顯然$h(j)$不可能含有$R$(因為$R$是未知的),所以
$$
h(j)=\left\{\begin{array}l
0,& j=0,1,\cdots,s-1;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s,s+1,\cdots,n.
\end{array}\right.
$$
即
$$
\widehat{p^s}=\frac{C_{n-s}^{T-s}}{C_{n}^T},\quad T=s,s+1,\cdots,n
$$
否則$\widehat{p^s}=0$。
對$p^s+(1-p)^s$也是一樣的步驟,等式寫成
$$
\sum_{j=0}^nh(j)C_n^jR^j(1-p)^n=p^s+(1-p)^{n-s},
$$
所以
$$
\sum_{j=0}^n h(j)C_n^jR^j=\sum_{k=0}^{n-s}C_{n-s}^k R^{s+k}+\sum_{l=0}^sC_s^l R^l=\sum_{j=0}^{s-1}C_s^jR^j+2R^s+\sum_{j={s+1}}^nC_{n-s}^{j-s}R^{j},
$$
故
$$
h(j)=\left\{\begin{array}l
\frac{C_s^j}{C_n^j},&j=0,1,\cdots,s-1;\\
\frac{2}{C_n^j},&j=s;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s+1,\cdots,n.
\end{array}\right.
$$
所以
$$
\widehat{p^s+(1-p)^{n-s}}=\left\{\begin{array}l
\dfrac{C_s^T}{C_n^T},&T=0,1,\cdots,s-1;\\
\dfrac{2}{C_n^T},&T=s;\\
\dfrac{C_{n-s}^{T-s}}{C_n^T},& T=s+1,\cdots,n.
\end{array}\right.
$$
## Part 4:無偏估計的條件期望
最後這種方法,比起待定係數法更巧一些。對於某些待估引數$g(\theta)$,如果它能用**某一事件的概率**來表示,就用樣本表示出這樣的事件$A$,於是$I_A$作為隨機變數的期望就是$\mathbb{E}(I_A)=\mathbb{P}(A)=g(\theta)$。在此基礎上,如果我們知道某個充分完備統計量$T$,就可以構造$h(T)=\mathbb{E}(I_A|T)$,$h(T)$就是$g(\theta)$的UMVUE。
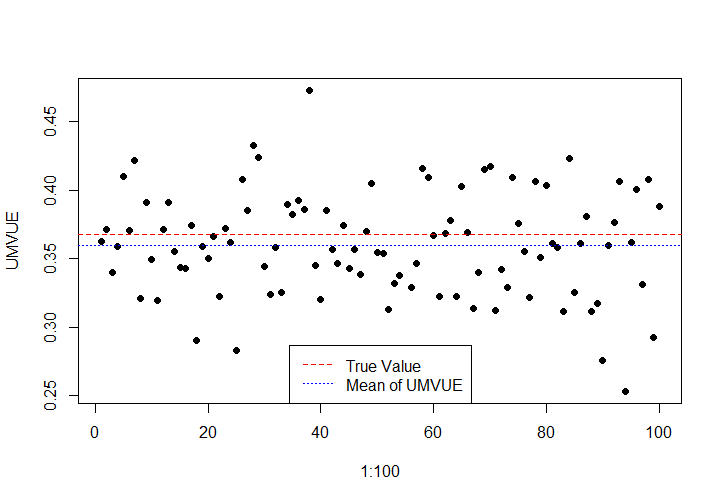
**第五題(36)** $X_1,\cdots,X_n$是從指數分佈$E(\lambda)$中抽取的簡單隨機樣本,對於給定的$\tau>
## Part 3:待定係數
有時候,無偏估計不是通過簡單的升次就能找到的,為了求出符合題意的$h(\cdot)$,可以使用待定係數法。待定係數法假定$h(\cdot)\in\mathcal P(\mathbb{R})$是一個多項式,從而根據次數關係確定$h(\cdot)$的各項係數,即使待估引數不是顯然的多項式,也可以通過泰勒展開變成多項式的形式(但一般很少這麼做)。
**第四題(33)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim B(1,p)$,求$p^s$的UMVUE和$p^s+(1-p)^{n-s}$的UMVUE。
容易驗證$p$的UMVUE是$T=\sum_{j=1}^nX_j\sim B(n,p)$,假定$h(T)$是$p^s$的UMVUE,則有
$$
\mathbb{E}[h(T)]=\sum_{j=0}^nh(j)C_{n}^j p^j(1-p)^{n-j}=p^s.
$$
左邊部分略顯繁瑣,對其進行整理,得到
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p}\right)^j(1-p)^n=p^s,
$$
所以
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p} \right)^j=\frac{p^s}{(1-p)^n}=\left(\frac{p}{1-p} \right)^s\left(\frac{1}{1-p} \right)^{n-s}.
$$
這裡要運用一個**二項分佈的常用換元**:
$$
R=\frac{p}{1-p}\Rightarrow p=\frac{R}{R+1},1-p=\frac{1}{R+1}.
$$
將等式兩邊變成
$$
\sum_{j=0}^n h(j)C_n^jR^j=R^s(1+R)^{n-s}=\sum_{k=0}^{n-s}C_{n-s}^kR^{s+k}=\sum_{k=s}^{n}C_{n-s}^{k-s}R^k.
$$
顯然$h(j)$不可能含有$R$(因為$R$是未知的),所以
$$
h(j)=\left\{\begin{array}l
0,& j=0,1,\cdots,s-1;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s,s+1,\cdots,n.
\end{array}\right.
$$
即
$$
\widehat{p^s}=\frac{C_{n-s}^{T-s}}{C_{n}^T},\quad T=s,s+1,\cdots,n
$$
否則$\widehat{p^s}=0$。
對$p^s+(1-p)^s$也是一樣的步驟,等式寫成
$$
\sum_{j=0}^nh(j)C_n^jR^j(1-p)^n=p^s+(1-p)^{n-s},
$$
所以
$$
\sum_{j=0}^n h(j)C_n^jR^j=\sum_{k=0}^{n-s}C_{n-s}^k R^{s+k}+\sum_{l=0}^sC_s^l R^l=\sum_{j=0}^{s-1}C_s^jR^j+2R^s+\sum_{j={s+1}}^nC_{n-s}^{j-s}R^{j},
$$
故
$$
h(j)=\left\{\begin{array}l
\frac{C_s^j}{C_n^j},&j=0,1,\cdots,s-1;\\
\frac{2}{C_n^j},&j=s;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s+1,\cdots,n.
\end{array}\right.
$$
所以
$$
\widehat{p^s+(1-p)^{n-s}}=\left\{\begin{array}l
\dfrac{C_s^T}{C_n^T},&T=0,1,\cdots,s-1;\\
\dfrac{2}{C_n^T},&T=s;\\
\dfrac{C_{n-s}^{T-s}}{C_n^T},& T=s+1,\cdots,n.
\end{array}\right.
$$
## Part 4:無偏估計的條件期望
最後這種方法,比起待定係數法更巧一些。對於某些待估引數$g(\theta)$,如果它能用**某一事件的概率**來表示,就用樣本表示出這樣的事件$A$,於是$I_A$作為隨機變數的期望就是$\mathbb{E}(I_A)=\mathbb{P}(A)=g(\theta)$。在此基礎上,如果我們知道某個充分完備統計量$T$,就可以構造$h(T)=\mathbb{E}(I_A|T)$,$h(T)$就是$g(\theta)$的UMVUE。
**第五題(36)** $X_1,\cdots,X_n$是從指數分佈$E(\lambda)$中抽取的簡單隨機樣本,對於給定的$\tau> 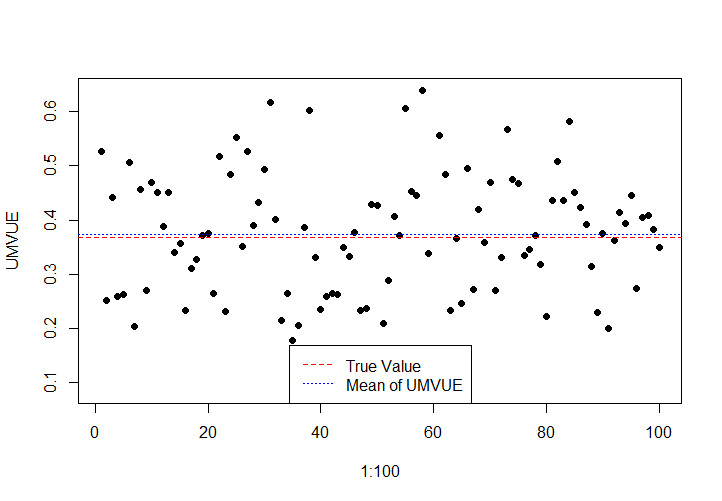 >
> 以下是$n=100$時的模擬結果:
>
>
>
> 以下是$n=100$時的模擬結果:
>
>  ---
上文中提到的UMVUE尋找方法,都是實踐中較為常用的方法,需要掌握。求出UMVUE後,可能還要計算其效率,驗證是否有效,這時候只要算出UMVUE的方差與C-R下界進行對比即可。
## 附程式碼
第一題:
```R
rm(list=ls())
mu.UMVUE <- c()
sigma2.UMVUE <- c()
mu <- 5
sigma <- 2
m <- 100
n <- 200
for (j in 1:100){
xlst <- rnorm(m, mu, sigma)
ylst <- rnorm(n, mu, sigma*sqrt(2))
T1 <- 2*sum(xlst^2) + sum(ylst^2)
T2 <- 2*sum(xlst) + sum(ylst)
mu.UMVUE[j] <- T2 / (2*m+n)
sigma2.UMVUE[j] <- (T2^2-(2*m+n)*T1) / (2*(2*m+n)*(1-m-n))
}
split.screen(c(1,2))
screen(1)
plot(1:100, mu.UMVUE)
abline(h=c(5), col="red", lty=2)
screen(2)
plot(1:100, sigma2.UMVUE)
abline(h=c(sigma^2), col='red', lty=2)
if (FALSE){
dev.off()
plot(mu.UMVUE, sigma2.UMVUE)
points(5, 4, col="red", cex=2, pch=20)
}
```
第三題:
```R
rm(list=ls())
n <- 10
UMVUE <- c()
for (j in 1:100){
xlst <- rnorm(n, 10, 6)
UMVUE[j] <- (n-2)/(n-1)*(mean(xlst)^2/var(xlst)-(n-1)/(n*(n-2)))
}
plot(1:100, UMVUE)
abline(h=c(100/36), col='red', lty=2)
abline(h=c(mean(UMVUE)), col='blue', lty=3)
legend("topleft", c("True value", "mean of UMVUE"), col=c("red", "blue"), lty=c(2, 3))
```
第五題:
```R
rm(list=ls())
lambda <- 3
tau <- 1/3
n <- 100
UMVUE <- c()
for (j in 1:100){
xlst <- rexp(n, lambda)
UMVUE[j] <- (1-tau/sum(xlst))^(n-1)
}
plot(1:100, UMVUE, pch=16)
abline(h=c(exp(-lambda*tau)), lty=2, col="red")
abline(h=c(mean(UMVUE)), lty=3, col="blue")
legend("bottom", c("True Value", "Mean of UMVUE"), col=c("red", "blue"), lty=c(2,
---
上文中提到的UMVUE尋找方法,都是實踐中較為常用的方法,需要掌握。求出UMVUE後,可能還要計算其效率,驗證是否有效,這時候只要算出UMVUE的方差與C-R下界進行對比即可。
## 附程式碼
第一題:
```R
rm(list=ls())
mu.UMVUE <- c()
sigma2.UMVUE <- c()
mu <- 5
sigma <- 2
m <- 100
n <- 200
for (j in 1:100){
xlst <- rnorm(m, mu, sigma)
ylst <- rnorm(n, mu, sigma*sqrt(2))
T1 <- 2*sum(xlst^2) + sum(ylst^2)
T2 <- 2*sum(xlst) + sum(ylst)
mu.UMVUE[j] <- T2 / (2*m+n)
sigma2.UMVUE[j] <- (T2^2-(2*m+n)*T1) / (2*(2*m+n)*(1-m-n))
}
split.screen(c(1,2))
screen(1)
plot(1:100, mu.UMVUE)
abline(h=c(5), col="red", lty=2)
screen(2)
plot(1:100, sigma2.UMVUE)
abline(h=c(sigma^2), col='red', lty=2)
if (FALSE){
dev.off()
plot(mu.UMVUE, sigma2.UMVUE)
points(5, 4, col="red", cex=2, pch=20)
}
```
第三題:
```R
rm(list=ls())
n <- 10
UMVUE <- c()
for (j in 1:100){
xlst <- rnorm(n, 10, 6)
UMVUE[j] <- (n-2)/(n-1)*(mean(xlst)^2/var(xlst)-(n-1)/(n*(n-2)))
}
plot(1:100, UMVUE)
abline(h=c(100/36), col='red', lty=2)
abline(h=c(mean(UMVUE)), col='blue', lty=3)
legend("topleft", c("True value", "mean of UMVUE"), col=c("red", "blue"), lty=c(2, 3))
```
第五題:
```R
rm(list=ls())
lambda <- 3
tau <- 1/3
n <- 100
UMVUE <- c()
for (j in 1:100){
xlst <- rexp(n, lambda)
UMVUE[j] <- (1-tau/sum(xlst))^(n-1)
}
plot(1:100, UMVUE, pch=16)
abline(h=c(exp(-lambda*tau)), lty=2, col="red")
abline(h=c(mean(UMVUE)), lty=3, col="blue")
legend("bottom", c("True Value", "Mean of UMVUE"), col=c("red", "blue"), lty=c(2,
 >
> 當$m=100,n=200$時,估計量示意圖為
>
>
>
> 當$m=100,n=200$時,估計量示意圖為
>
>  >
> 繪製在一張圖上:
>
>
>
> 繪製在一張圖上:
>
>  >
> 程式碼見附錄。
## Part 2:無偏修正
由於尋找充分完備統計量的過程比較機械,許多時候難點並不在此,而是在於將充分完備統計量進行一定的變換,得到充分完備統計量的無偏函式估計。其關鍵,就在於將充分完備統計量進行一定的次數變換,達到待估引數所需的次數。
**第二題(31)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim N(0,\sigma^2)$,求$\sigma$和$\sigma^4$的UMVUE。
均值已知,容易求得$\sigma^2$的充分完備統計量就是
$$
T=\sum_{j=1}^n X_j^2.
$$
關鍵在於找到合適的$h(\cdot)$,使得$\mathbb{E}(h(T))=\sigma$,或者$\mathbb{E}(h(T))=\sigma^4$。顯然,我們會從$\sqrt{T}$和$T^2$上入手,因此,我們需要先給出$T$的密度,才能求其函式的期望。容易發現
$$
\frac{T}{\sigma^2}=\sum_{j=1}^n\left(\frac{X_j}{\sigma} \right)^2\sim \chi^2(n)\Rightarrow T\sim \Gamma\left(\frac{n}{2},\frac{1}{2\sigma^2} \right),
$$
所以$T$的密度函式是
$$
p(t)=\frac{I_{t>
>
> 程式碼見附錄。
## Part 2:無偏修正
由於尋找充分完備統計量的過程比較機械,許多時候難點並不在此,而是在於將充分完備統計量進行一定的變換,得到充分完備統計量的無偏函式估計。其關鍵,就在於將充分完備統計量進行一定的次數變換,達到待估引數所需的次數。
**第二題(31)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim N(0,\sigma^2)$,求$\sigma$和$\sigma^4$的UMVUE。
均值已知,容易求得$\sigma^2$的充分完備統計量就是
$$
T=\sum_{j=1}^n X_j^2.
$$
關鍵在於找到合適的$h(\cdot)$,使得$\mathbb{E}(h(T))=\sigma$,或者$\mathbb{E}(h(T))=\sigma^4$。顯然,我們會從$\sqrt{T}$和$T^2$上入手,因此,我們需要先給出$T$的密度,才能求其函式的期望。容易發現
$$
\frac{T}{\sigma^2}=\sum_{j=1}^n\left(\frac{X_j}{\sigma} \right)^2\sim \chi^2(n)\Rightarrow T\sim \Gamma\left(\frac{n}{2},\frac{1}{2\sigma^2} \right),
$$
所以$T$的密度函式是
$$
p(t)=\frac{I_{t> ## Part 3:待定係數
有時候,無偏估計不是通過簡單的升次就能找到的,為了求出符合題意的$h(\cdot)$,可以使用待定係數法。待定係數法假定$h(\cdot)\in\mathcal P(\mathbb{R})$是一個多項式,從而根據次數關係確定$h(\cdot)$的各項係數,即使待估引數不是顯然的多項式,也可以通過泰勒展開變成多項式的形式(但一般很少這麼做)。
**第四題(33)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim B(1,p)$,求$p^s$的UMVUE和$p^s+(1-p)^{n-s}$的UMVUE。
容易驗證$p$的UMVUE是$T=\sum_{j=1}^nX_j\sim B(n,p)$,假定$h(T)$是$p^s$的UMVUE,則有
$$
\mathbb{E}[h(T)]=\sum_{j=0}^nh(j)C_{n}^j p^j(1-p)^{n-j}=p^s.
$$
左邊部分略顯繁瑣,對其進行整理,得到
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p}\right)^j(1-p)^n=p^s,
$$
所以
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p} \right)^j=\frac{p^s}{(1-p)^n}=\left(\frac{p}{1-p} \right)^s\left(\frac{1}{1-p} \right)^{n-s}.
$$
這裡要運用一個**二項分佈的常用換元**:
$$
R=\frac{p}{1-p}\Rightarrow p=\frac{R}{R+1},1-p=\frac{1}{R+1}.
$$
將等式兩邊變成
$$
\sum_{j=0}^n h(j)C_n^jR^j=R^s(1+R)^{n-s}=\sum_{k=0}^{n-s}C_{n-s}^kR^{s+k}=\sum_{k=s}^{n}C_{n-s}^{k-s}R^k.
$$
顯然$h(j)$不可能含有$R$(因為$R$是未知的),所以
$$
h(j)=\left\{\begin{array}l
0,& j=0,1,\cdots,s-1;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s,s+1,\cdots,n.
\end{array}\right.
$$
即
$$
\widehat{p^s}=\frac{C_{n-s}^{T-s}}{C_{n}^T},\quad T=s,s+1,\cdots,n
$$
否則$\widehat{p^s}=0$。
對$p^s+(1-p)^s$也是一樣的步驟,等式寫成
$$
\sum_{j=0}^nh(j)C_n^jR^j(1-p)^n=p^s+(1-p)^{n-s},
$$
所以
$$
\sum_{j=0}^n h(j)C_n^jR^j=\sum_{k=0}^{n-s}C_{n-s}^k R^{s+k}+\sum_{l=0}^sC_s^l R^l=\sum_{j=0}^{s-1}C_s^jR^j+2R^s+\sum_{j={s+1}}^nC_{n-s}^{j-s}R^{j},
$$
故
$$
h(j)=\left\{\begin{array}l
\frac{C_s^j}{C_n^j},&j=0,1,\cdots,s-1;\\
\frac{2}{C_n^j},&j=s;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s+1,\cdots,n.
\end{array}\right.
$$
所以
$$
\widehat{p^s+(1-p)^{n-s}}=\left\{\begin{array}l
\dfrac{C_s^T}{C_n^T},&T=0,1,\cdots,s-1;\\
\dfrac{2}{C_n^T},&T=s;\\
\dfrac{C_{n-s}^{T-s}}{C_n^T},& T=s+1,\cdots,n.
\end{array}\right.
$$
## Part 4:無偏估計的條件期望
最後這種方法,比起待定係數法更巧一些。對於某些待估引數$g(\theta)$,如果它能用**某一事件的概率**來表示,就用樣本表示出這樣的事件$A$,於是$I_A$作為隨機變數的期望就是$\mathbb{E}(I_A)=\mathbb{P}(A)=g(\theta)$。在此基礎上,如果我們知道某個充分完備統計量$T$,就可以構造$h(T)=\mathbb{E}(I_A|T)$,$h(T)$就是$g(\theta)$的UMVUE。
**第五題(36)** $X_1,\cdots,X_n$是從指數分佈$E(\lambda)$中抽取的簡單隨機樣本,對於給定的$\tau>
## Part 3:待定係數
有時候,無偏估計不是通過簡單的升次就能找到的,為了求出符合題意的$h(\cdot)$,可以使用待定係數法。待定係數法假定$h(\cdot)\in\mathcal P(\mathbb{R})$是一個多項式,從而根據次數關係確定$h(\cdot)$的各項係數,即使待估引數不是顯然的多項式,也可以通過泰勒展開變成多項式的形式(但一般很少這麼做)。
**第四題(33)** 設$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim B(1,p)$,求$p^s$的UMVUE和$p^s+(1-p)^{n-s}$的UMVUE。
容易驗證$p$的UMVUE是$T=\sum_{j=1}^nX_j\sim B(n,p)$,假定$h(T)$是$p^s$的UMVUE,則有
$$
\mathbb{E}[h(T)]=\sum_{j=0}^nh(j)C_{n}^j p^j(1-p)^{n-j}=p^s.
$$
左邊部分略顯繁瑣,對其進行整理,得到
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p}\right)^j(1-p)^n=p^s,
$$
所以
$$
\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p} \right)^j=\frac{p^s}{(1-p)^n}=\left(\frac{p}{1-p} \right)^s\left(\frac{1}{1-p} \right)^{n-s}.
$$
這裡要運用一個**二項分佈的常用換元**:
$$
R=\frac{p}{1-p}\Rightarrow p=\frac{R}{R+1},1-p=\frac{1}{R+1}.
$$
將等式兩邊變成
$$
\sum_{j=0}^n h(j)C_n^jR^j=R^s(1+R)^{n-s}=\sum_{k=0}^{n-s}C_{n-s}^kR^{s+k}=\sum_{k=s}^{n}C_{n-s}^{k-s}R^k.
$$
顯然$h(j)$不可能含有$R$(因為$R$是未知的),所以
$$
h(j)=\left\{\begin{array}l
0,& j=0,1,\cdots,s-1;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s,s+1,\cdots,n.
\end{array}\right.
$$
即
$$
\widehat{p^s}=\frac{C_{n-s}^{T-s}}{C_{n}^T},\quad T=s,s+1,\cdots,n
$$
否則$\widehat{p^s}=0$。
對$p^s+(1-p)^s$也是一樣的步驟,等式寫成
$$
\sum_{j=0}^nh(j)C_n^jR^j(1-p)^n=p^s+(1-p)^{n-s},
$$
所以
$$
\sum_{j=0}^n h(j)C_n^jR^j=\sum_{k=0}^{n-s}C_{n-s}^k R^{s+k}+\sum_{l=0}^sC_s^l R^l=\sum_{j=0}^{s-1}C_s^jR^j+2R^s+\sum_{j={s+1}}^nC_{n-s}^{j-s}R^{j},
$$
故
$$
h(j)=\left\{\begin{array}l
\frac{C_s^j}{C_n^j},&j=0,1,\cdots,s-1;\\
\frac{2}{C_n^j},&j=s;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s+1,\cdots,n.
\end{array}\right.
$$
所以
$$
\widehat{p^s+(1-p)^{n-s}}=\left\{\begin{array}l
\dfrac{C_s^T}{C_n^T},&T=0,1,\cdots,s-1;\\
\dfrac{2}{C_n^T},&T=s;\\
\dfrac{C_{n-s}^{T-s}}{C_n^T},& T=s+1,\cdots,n.
\end{array}\right.
$$
## Part 4:無偏估計的條件期望
最後這種方法,比起待定係數法更巧一些。對於某些待估引數$g(\theta)$,如果它能用**某一事件的概率**來表示,就用樣本表示出這樣的事件$A$,於是$I_A$作為隨機變數的期望就是$\mathbb{E}(I_A)=\mathbb{P}(A)=g(\theta)$。在此基礎上,如果我們知道某個充分完備統計量$T$,就可以構造$h(T)=\mathbb{E}(I_A|T)$,$h(T)$就是$g(\theta)$的UMVUE。
**第五題(36)** $X_1,\cdots,X_n$是從指數分佈$E(\lambda)$中抽取的簡單隨機樣本,對於給定的$\tau> >
> 以下是$n=100$時的模擬結果:
>
>
>
> 以下是$n=100$時的模擬結果:
>
>  ---
上文中提到的UMVUE尋找方法,都是實踐中較為常用的方法,需要掌握。求出UMVUE後,可能還要計算其效率,驗證是否有效,這時候只要算出UMVUE的方差與C-R下界進行對比即可。
## 附程式碼
第一題:
```R
rm(list=ls())
mu.UMVUE <- c()
sigma2.UMVUE <- c()
mu <- 5
sigma <- 2
m <- 100
n <- 200
for (j in 1:100){
xlst <- rnorm(m, mu, sigma)
ylst <- rnorm(n, mu, sigma*sqrt(2))
T1 <- 2*sum(xlst^2) + sum(ylst^2)
T2 <- 2*sum(xlst) + sum(ylst)
mu.UMVUE[j] <- T2 / (2*m+n)
sigma2.UMVUE[j] <- (T2^2-(2*m+n)*T1) / (2*(2*m+n)*(1-m-n))
}
split.screen(c(1,2))
screen(1)
plot(1:100, mu.UMVUE)
abline(h=c(5), col="red", lty=2)
screen(2)
plot(1:100, sigma2.UMVUE)
abline(h=c(sigma^2), col='red', lty=2)
if (FALSE){
dev.off()
plot(mu.UMVUE, sigma2.UMVUE)
points(5, 4, col="red", cex=2, pch=20)
}
```
第三題:
```R
rm(list=ls())
n <- 10
UMVUE <- c()
for (j in 1:100){
xlst <- rnorm(n, 10, 6)
UMVUE[j] <- (n-2)/(n-1)*(mean(xlst)^2/var(xlst)-(n-1)/(n*(n-2)))
}
plot(1:100, UMVUE)
abline(h=c(100/36), col='red', lty=2)
abline(h=c(mean(UMVUE)), col='blue', lty=3)
legend("topleft", c("True value", "mean of UMVUE"), col=c("red", "blue"), lty=c(2, 3))
```
第五題:
```R
rm(list=ls())
lambda <- 3
tau <- 1/3
n <- 100
UMVUE <- c()
for (j in 1:100){
xlst <- rexp(n, lambda)
UMVUE[j] <- (1-tau/sum(xlst))^(n-1)
}
plot(1:100, UMVUE, pch=16)
abline(h=c(exp(-lambda*tau)), lty=2, col="red")
abline(h=c(mean(UMVUE)), lty=3, col="blue")
legend("bottom", c("True Value", "Mean of UMVUE"), col=c("red", "blue"), lty=c(2,
---
上文中提到的UMVUE尋找方法,都是實踐中較為常用的方法,需要掌握。求出UMVUE後,可能還要計算其效率,驗證是否有效,這時候只要算出UMVUE的方差與C-R下界進行對比即可。
## 附程式碼
第一題:
```R
rm(list=ls())
mu.UMVUE <- c()
sigma2.UMVUE <- c()
mu <- 5
sigma <- 2
m <- 100
n <- 200
for (j in 1:100){
xlst <- rnorm(m, mu, sigma)
ylst <- rnorm(n, mu, sigma*sqrt(2))
T1 <- 2*sum(xlst^2) + sum(ylst^2)
T2 <- 2*sum(xlst) + sum(ylst)
mu.UMVUE[j] <- T2 / (2*m+n)
sigma2.UMVUE[j] <- (T2^2-(2*m+n)*T1) / (2*(2*m+n)*(1-m-n))
}
split.screen(c(1,2))
screen(1)
plot(1:100, mu.UMVUE)
abline(h=c(5), col="red", lty=2)
screen(2)
plot(1:100, sigma2.UMVUE)
abline(h=c(sigma^2), col='red', lty=2)
if (FALSE){
dev.off()
plot(mu.UMVUE, sigma2.UMVUE)
points(5, 4, col="red", cex=2, pch=20)
}
```
第三題:
```R
rm(list=ls())
n <- 10
UMVUE <- c()
for (j in 1:100){
xlst <- rnorm(n, 10, 6)
UMVUE[j] <- (n-2)/(n-1)*(mean(xlst)^2/var(xlst)-(n-1)/(n*(n-2)))
}
plot(1:100, UMVUE)
abline(h=c(100/36), col='red', lty=2)
abline(h=c(mean(UMVUE)), col='blue', lty=3)
legend("topleft", c("True value", "mean of UMVUE"), col=c("red", "blue"), lty=c(2, 3))
```
第五題:
```R
rm(list=ls())
lambda <- 3
tau <- 1/3
n <- 100
UMVUE <- c()
for (j in 1:100){
xlst <- rexp(n, lambda)
UMVUE[j] <- (1-tau/sum(xlst))^(n-1)
}
plot(1:100, UMVUE, pch=16)
abline(h=c(exp(-lambda*tau)), lty=2, col="red")
abline(h=c(mean(UMVUE)), lty=3, col="blue")
legend("bottom", c("True Value", "Mean of UMVUE"), col=c("red", "blue"), lty=c(2,
