利用CORDIC演算法計算三角函式
阿新 • • 發佈：2021-03-03
這裡主要先介紹如何利用CORDIC演算法計算固定角度$\phi$的$cos(\phi)$、$sin(\phi)$值。參考了這兩篇文章[[1]](https://mp.weixin.qq.com/s/c4oro0bOhdDUmBt0yyLpTA)、[[2]](https://blog.csdn.net/qq_39210023/article/details/77456031)。
一般利用MATLAB計算三角函式時，用$cos$舉例，只需要輸入相應的$cos(\phi)$便自動計算出來了。但是如果是硬體處理或者沒有那麼方便的函式時，該如何計算$cos(\phi)$的值呢？
有一種最傻瓜的方式是用rom儲存$0^o$到$90^o$所有的餘弦值，然後用查表的方法計算，但隨著精度要求的提升，需要儲存的值會越來越多，這是不合適的。那麼有沒有一種用較少資源且能較快計算出高精度三角函式值的方法呢？有！這就是CORDIC演算法可以做的事，演算法不難，有一點三角函式和移位運算的基礎就能看懂了，核心思想就是把乘法運算變成移位運算。下面來仔細講解。
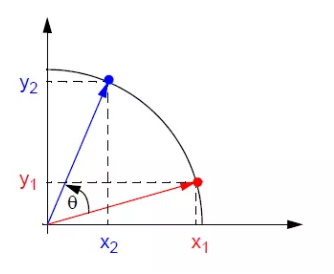首先引入一個在圓上的座標旋轉公式（不一定單位圓）
$$
\begin{cases}
x_2 = x_1cos\theta - y_1sin\theta \\
y_2 = x_1sin\theta + y_1cos\theta \tag{1}\\
\end{cases}
$$
那麼如何求$cos\phi$和$sin\phi$呢？我們可以看出，如果讓初始座標$(x_1, y_1)$取$x$軸一個特定的位置，最後使其旋轉$\phi^o$到座標$(x_n,y_n)$處，且滿足$\sqrt{x_n^2 + y_n^2} = 1$，那麼$cos\phi$不就等於$x_n$，$sin\phi$不就等於$y_n$了。這是後話，我們繼續看式$(1)$，$(1)$也可以寫成：
$$
\begin{cases}
x_2 = cos\theta(x_1 - y_1tan\theta) \\
y_2 = cos\theta(y_1 + x_1tan\theta)\tag{2} \\
\end{cases}
$$
由於對$(x_2, y_2)$相當於同乘了一個常數$cos\theta$，我們先不看它，不影響旋轉角度，得到：
$$
\begin{cases}
x_2 = x_1 - y_1tan\theta \\
y_2 = y_1 + x_1tan\theta \tag{3} \\
\end{cases}
$$
### 一：乘法變移位 之前說的我們要把乘法運算變成移位運算，所以我們找到$tan\theta$與$2^{-i}$之間的對應關係，注意由於是變成移位操作，所以對應旋轉的角度也是幾個固定的值，但是通過旋轉這幾個固定的角度，旋轉$i$次，最終也一定能轉到我們需要的角度$\phi$上($-99.7^o\le\phi \le 99.7^o$)。
### 二：cos累乘項 現在考慮把$cos\theta$加回去，回到$(2)$，且考慮旋轉方向$d_i$和旋轉角度$\theta_i$，得到： $$ \begin{cases} x_2 = cos\theta_1(x_1 - d_1y_1tan\theta_1) \\ y_2 = cos\theta_1(y_1 + d_1x_1tan\theta_1)\tag{5.1} \\ \end{cases} $$ 進行下一次迭代(旋轉)，得到： $$ \begin{align} x_3 &= cos\theta_2(x_2 - d_2y_2tan\theta_2) \\ &= cos\theta_2(cos\theta_1(x_1 - d_1y_1tan\theta_1)- d_2cos\theta_1(y_1 + d_1x_1tan\theta_1)tan\theta_2) \\ &= cos\theta_1cos\theta_2(x_1 - d_1y_1tan\theta_1 - d_2y_1tan\theta_2 - d_2d_1x_1tan\theta_1tan\theta_2) \end{align} \\ $$ $$ \begin{align} y_3 &= cos\theta_2(y_2 + d_2x_2tan\theta_2) \\ &= cos\theta_2(cos\theta_1(y_1 + d_1x_1tan\theta_1) + d_2cos\theta_1(x_1 - d_1y_1tan\theta_1)tan\theta_2) \tag{5.2}\\ &= cos\theta_1cos\theta_2(y_1 + d_1x_1tan\theta_1 + d_2x_1tan\theta_2 - d_2d_1y_1tan\theta_1tan\theta_2) \end{align} $$ 可以看到每次旋轉都可以提取出$cos\theta_i$。$tan\theta_i$已經用移位替代了。接下來只用計算$\prod_{i=1}^{N}cos\theta_i$就行了，且$\prod_{i=1}^{N}cos\theta_i$只跟迭代次數有關，確定了迭代次數後，可以預先把$\prod_{i=1}^{N}cos\theta_i$算出來。
### 三：累計旋轉角度與旋轉方向 現在考慮最後一個問題，如何確定每次迭代的旋轉方向$d_i$呢？其實定義一個累計旋轉角度$z_i$ $$z_{i + 1} = z_i -d_i\theta_i = z_i -d_i2^{-i} \tag{6}$$ 令$z_1$等於目標角度值，然後每次迭代作個判斷就好，如果$z_i > 0$，說明當前旋轉還沒轉到目標角度，$d_{i+1} = 1$；如果$z_i < 0$，說明當前旋轉超過了目標角度，$d_{i+1} = -1$。 當我們最終轉到了目標角度$\phi$時，比如$\phi = 66^o$，可以此時$z_i$已經很小趨近於零了。 另外，在作比較判斷時，單次旋轉角度$\theta_i$則還是需要通過查一次$arctan(2^{-i})$表得到，但這個表比起文章開頭說的傻瓜式查表要小太多了。
### 四：計算cos和sin值 進行差不多十多次迭代，最後趨近到所需旋轉角度$\phi$時，最後一個座標可由如下公式計算： $$ \begin{cases} x(n) = \frac{1}{\prod_{i=1}^n cos\theta_i}(x(1)cosz_1 - y(1)sinz_1 \\ y(n) = \frac{1}{\prod_{i=1}^n cos\theta_i}(y(1)cosz_1 + x(1)sinz_1 \tag{7} \end{cases} $$ 關於公式$(6)$是如何通過公式$(2)(3)(4)(5)$推出來的，暫時還不太理解。但是我們從公式$(6)$可以看出，當我們設定初始座標$(x_1, y_1) = (\prod_{i=1}^n cos\theta_i, 0)$，再另初始累計旋轉角度$z_1 = \phi$時： $$ \begin{cases} cos\phi = x(n) \\ sin\phi = y(n) \tag{8} \end{cases} $$ 這樣就只用通過$(4)(6)$的移位、相加、一次查表，再迭代十多次，就能計算$cos\phi$和$\sin\phi$值啦！ 其實用CORDIC演算法還能計算arctan、sinh、cosh等值，以後學習了再來補充進階版。
### 五：完整MATLAB程式碼 ``` clc, clear, close all; %% 初始計算cos累乘值 N = 16; % 設定迭代次數16次 Nprod(1) = 1; for i = 1 : N Nprod(i + 1) = Nprod(i) * cos(atan(2^(-(i - 1)))); end %% Cordic演算法計算cos、sin值 x(1) = Nprod(N); % 橫座標初始值賦為cos累乘值，公式(7) y(1) = 0; % 縱座標初始值賦為0，公式(7) z(1) = 66 / 180 * pi; %目標旋轉角度值，66°，注意轉化成弧度值 d(1) = 1; %旋轉方向，初始肯定為1 for i = 1 : N x(i + 1) = x(i) - d(i) * y(i) * 2^(-(i - 1)); %移位運算，公式(4) y(i + 1) = y(i) + d(i) * x(i) * 2^(-(i - 1)); %移位運算，公式(4) z(i + 1) = z(i) - d(i) * atan(2^(-(i - 1))); %計算累計旋轉角度，查一次表，公式(6) if z(i + 1) >= 0 % 判斷下一次的旋轉方向 d(i + 1) = 1; else d(i + 1) = -1; end end COS = x(N) % 輸出cos66的值 SIN = y(N) % 輸出sin66的值 ```
### 六：參考文章 [1]：
首先引入一個在圓上的座標旋轉公式（不一定單位圓）
$$
\begin{cases}
x_2 = x_1cos\theta - y_1sin\theta \\
y_2 = x_1sin\theta + y_1cos\theta \tag{1}\\
\end{cases}
$$
那麼如何求$cos\phi$和$sin\phi$呢？我們可以看出，如果讓初始座標$(x_1, y_1)$取$x$軸一個特定的位置，最後使其旋轉$\phi^o$到座標$(x_n,y_n)$處，且滿足$\sqrt{x_n^2 + y_n^2} = 1$，那麼$cos\phi$不就等於$x_n$，$sin\phi$不就等於$y_n$了。這是後話，我們繼續看式$(1)$，$(1)$也可以寫成：
$$
\begin{cases}
x_2 = cos\theta(x_1 - y_1tan\theta) \\
y_2 = cos\theta(y_1 + x_1tan\theta)\tag{2} \\
\end{cases}
$$
由於對$(x_2, y_2)$相當於同乘了一個常數$cos\theta$，我們先不看它，不影響旋轉角度，得到：
$$
\begin{cases}
x_2 = x_1 - y_1tan\theta \\
y_2 = y_1 + x_1tan\theta \tag{3} \\
\end{cases}
$$
### 一：乘法變移位 之前說的我們要把乘法運算變成移位運算，所以我們找到$tan\theta$與$2^{-i}$之間的對應關係，注意由於是變成移位操作，所以對應旋轉的角度也是幾個固定的值，但是通過旋轉這幾個固定的角度，旋轉$i$次，最終也一定能轉到我們需要的角度$\phi$上($-99.7^o\le\phi \le 99.7^o$)。
### 二：cos累乘項 現在考慮把$cos\theta$加回去，回到$(2)$，且考慮旋轉方向$d_i$和旋轉角度$\theta_i$，得到： $$ \begin{cases} x_2 = cos\theta_1(x_1 - d_1y_1tan\theta_1) \\ y_2 = cos\theta_1(y_1 + d_1x_1tan\theta_1)\tag{5.1} \\ \end{cases} $$ 進行下一次迭代(旋轉)，得到： $$ \begin{align} x_3 &= cos\theta_2(x_2 - d_2y_2tan\theta_2) \\ &= cos\theta_2(cos\theta_1(x_1 - d_1y_1tan\theta_1)- d_2cos\theta_1(y_1 + d_1x_1tan\theta_1)tan\theta_2) \\ &= cos\theta_1cos\theta_2(x_1 - d_1y_1tan\theta_1 - d_2y_1tan\theta_2 - d_2d_1x_1tan\theta_1tan\theta_2) \end{align} \\ $$ $$ \begin{align} y_3 &= cos\theta_2(y_2 + d_2x_2tan\theta_2) \\ &= cos\theta_2(cos\theta_1(y_1 + d_1x_1tan\theta_1) + d_2cos\theta_1(x_1 - d_1y_1tan\theta_1)tan\theta_2) \tag{5.2}\\ &= cos\theta_1cos\theta_2(y_1 + d_1x_1tan\theta_1 + d_2x_1tan\theta_2 - d_2d_1y_1tan\theta_1tan\theta_2) \end{align} $$ 可以看到每次旋轉都可以提取出$cos\theta_i$。$tan\theta_i$已經用移位替代了。接下來只用計算$\prod_{i=1}^{N}cos\theta_i$就行了，且$\prod_{i=1}^{N}cos\theta_i$只跟迭代次數有關，確定了迭代次數後，可以預先把$\prod_{i=1}^{N}cos\theta_i$算出來。
### 三：累計旋轉角度與旋轉方向 現在考慮最後一個問題，如何確定每次迭代的旋轉方向$d_i$呢？其實定義一個累計旋轉角度$z_i$ $$z_{i + 1} = z_i -d_i\theta_i = z_i -d_i2^{-i} \tag{6}$$ 令$z_1$等於目標角度值，然後每次迭代作個判斷就好，如果$z_i > 0$，說明當前旋轉還沒轉到目標角度，$d_{i+1} = 1$；如果$z_i < 0$，說明當前旋轉超過了目標角度，$d_{i+1} = -1$。 當我們最終轉到了目標角度$\phi$時，比如$\phi = 66^o$，可以此時$z_i$已經很小趨近於零了。 另外，在作比較判斷時，單次旋轉角度$\theta_i$則還是需要通過查一次$arctan(2^{-i})$表得到，但這個表比起文章開頭說的傻瓜式查表要小太多了。
### 四：計算cos和sin值 進行差不多十多次迭代，最後趨近到所需旋轉角度$\phi$時，最後一個座標可由如下公式計算： $$ \begin{cases} x(n) = \frac{1}{\prod_{i=1}^n cos\theta_i}(x(1)cosz_1 - y(1)sinz_1 \\ y(n) = \frac{1}{\prod_{i=1}^n cos\theta_i}(y(1)cosz_1 + x(1)sinz_1 \tag{7} \end{cases} $$ 關於公式$(6)$是如何通過公式$(2)(3)(4)(5)$推出來的，暫時還不太理解。但是我們從公式$(6)$可以看出，當我們設定初始座標$(x_1, y_1) = (\prod_{i=1}^n cos\theta_i, 0)$，再另初始累計旋轉角度$z_1 = \phi$時： $$ \begin{cases} cos\phi = x(n) \\ sin\phi = y(n) \tag{8} \end{cases} $$ 這樣就只用通過$(4)(6)$的移位、相加、一次查表，再迭代十多次，就能計算$cos\phi$和$\sin\phi$值啦！ 其實用CORDIC演算法還能計算arctan、sinh、cosh等值，以後學習了再來補充進階版。
### 五：完整MATLAB程式碼 ``` clc, clear, close all; %% 初始計算cos累乘值 N = 16; % 設定迭代次數16次 Nprod(1) = 1; for i = 1 : N Nprod(i + 1) = Nprod(i) * cos(atan(2^(-(i - 1)))); end %% Cordic演算法計算cos、sin值 x(1) = Nprod(N); % 橫座標初始值賦為cos累乘值，公式(7) y(1) = 0; % 縱座標初始值賦為0，公式(7) z(1) = 66 / 180 * pi; %目標旋轉角度值，66°，注意轉化成弧度值 d(1) = 1; %旋轉方向，初始肯定為1 for i = 1 : N x(i + 1) = x(i) - d(i) * y(i) * 2^(-(i - 1)); %移位運算，公式(4) y(i + 1) = y(i) + d(i) * x(i) * 2^(-(i - 1)); %移位運算，公式(4) z(i + 1) = z(i) - d(i) * atan(2^(-(i - 1))); %計算累計旋轉角度，查一次表，公式(6) if z(i + 1) >= 0 % 判斷下一次的旋轉方向 d(i + 1) = 1; else d(i + 1) = -1; end end COS = x(N) % 輸出cos66的值 SIN = y(N) % 輸出sin66的值 ```
### 六：參考文章 [1]：