WPF3D立方體圖形展開動畫思路
阿新 • • 發佈:2021-03-30
# WPF3D立方體圖形展開動畫
**效果圖:**
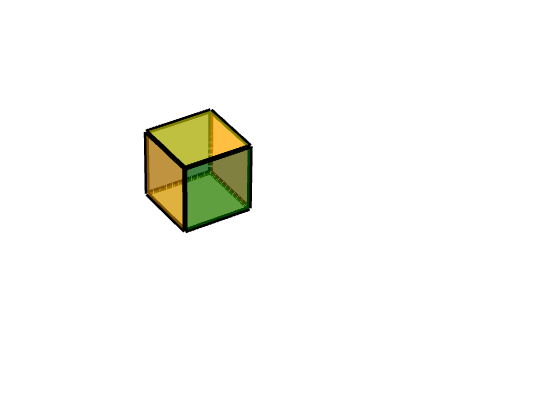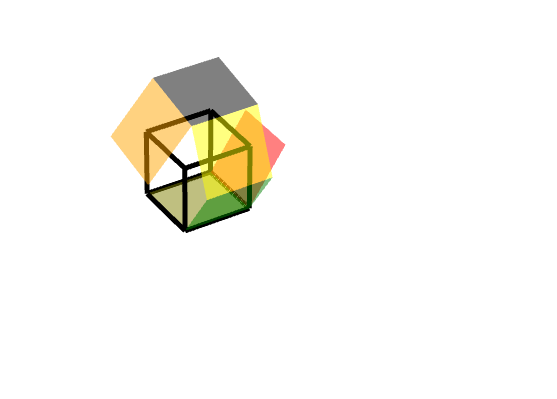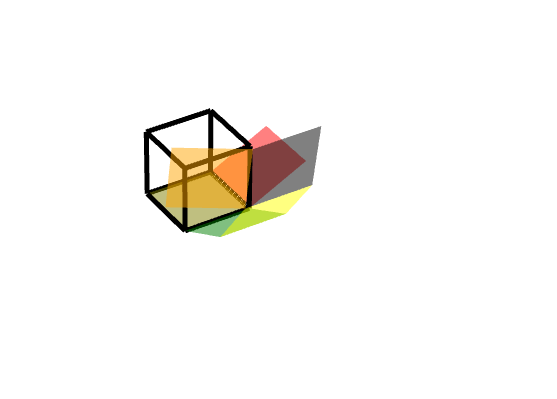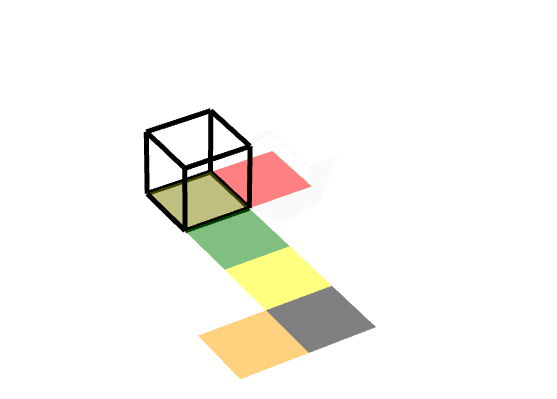
##### 規定:
立方體中心為(000),稜長為2,則(111)(-1-1-1)等1,-1三維組合的八個點為其頂點
**座標系:**
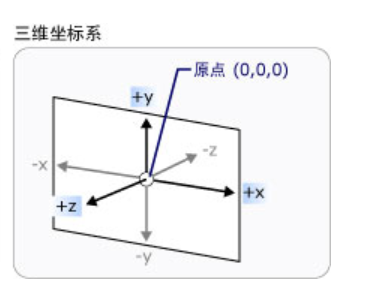
**補充:**
WPF 3D 分為**中心對稱旋轉**([RotateTransform3D](https://docs.microsoft.com/en-us/dotnet/api/system.windows.media.media3d.rotatetransform3d)),**平移旋轉**([TranslateTransform3D](https://docs.microsoft.com/en-us/dotnet/api/system.windows.media.media3d.translatetransform3d))和**比例縮減**([ScaleTransform3D](https://docs.microsoft.com/en-us/dotnet/api/system.windows.media.media3d.scaletransform3d)),立體圖形展開目前只用到**對稱和平移變換**
## 1 按軸旋轉的面
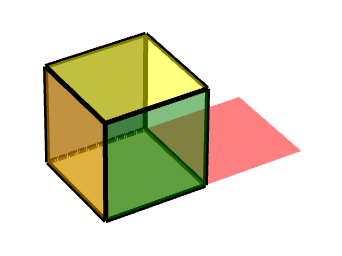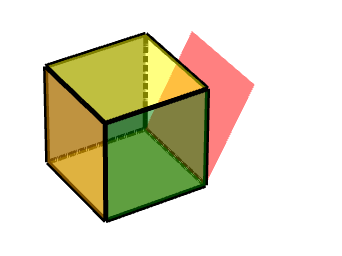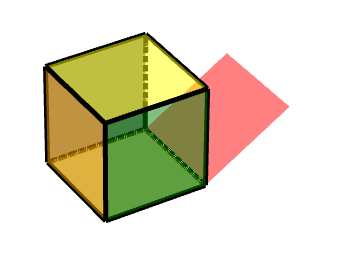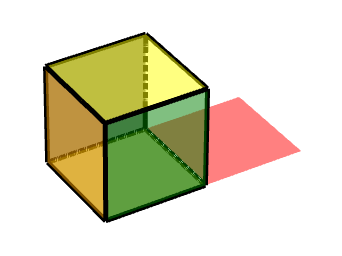
如圖所示,則其是按照由(-1-1-1)到(1-1-1)的軸運動
換算成中心對稱,也就是這條邊的中點,則對稱點為(0,-1,-1)
***此動畫可描述為,對點(0,-1,-1)做中心對稱變換,沿X軸旋轉90度。***
Code:
```c#
//設定對稱中心
face0RotateTransform3D.CenterX = 0;
face0RotateTransform3D.CenterY = -1;
face0RotateTransform3D.CenterZ = -1;
//設定旋轉角度
(face0RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(1, 0, 0);
DoubleAnimation face0AxisAngleRotation3DAnimation = new DoubleAnimation();
face0AxisAngleRotation3DAnimation.From = 0;
face0AxisAngleRotation3DAnimation.To = -90;
face0AxisAngleRotation3DAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));
```
同理可得另一個面:***對點(1,-1,-1)做中心對稱變換,沿Z軸旋轉90度。***
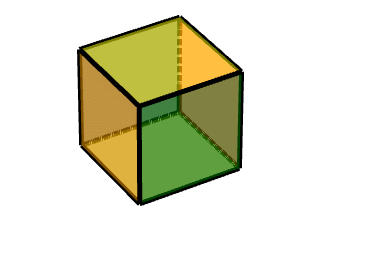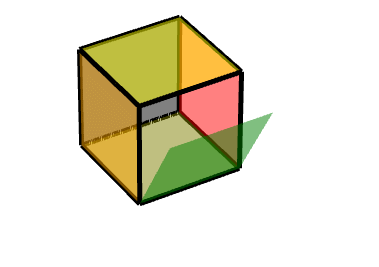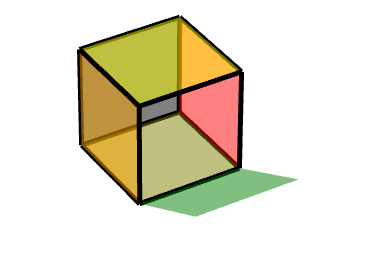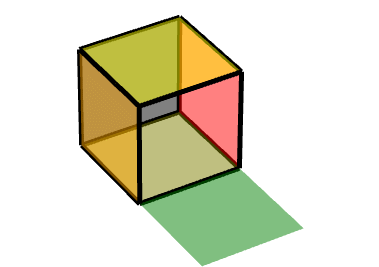
Code:
```c#
face3RotateTransform3D.CenterX = 1;
face3RotateTransform3D.CenterY = -1;
face3RotateTransform3D.CenterZ = -1;
(face3RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -90;
```
## 2 連線按軸旋轉的面的面
即二級旋轉面
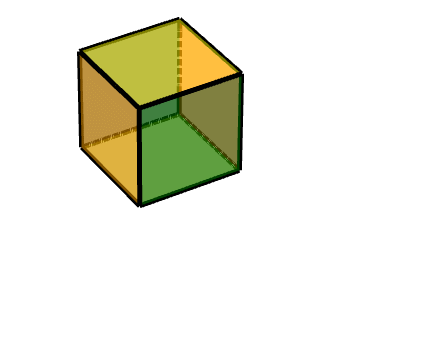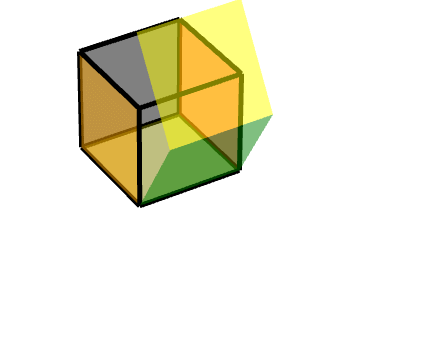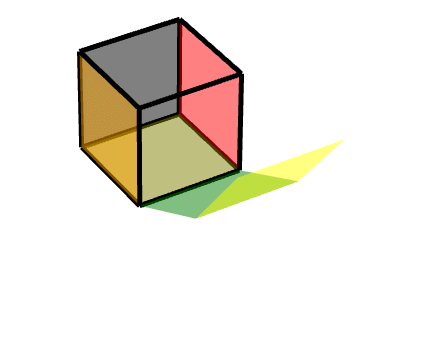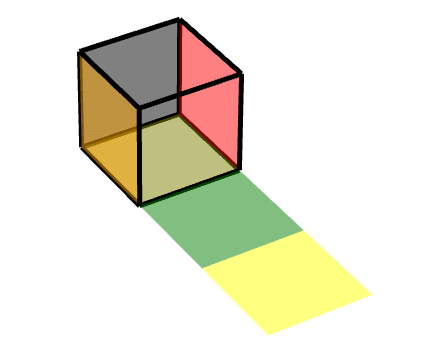
此時,我們可以把它理解為兩個旋轉的結合,**一個軸對稱旋轉+一個平移旋轉**
###### 1 軸對稱旋轉:
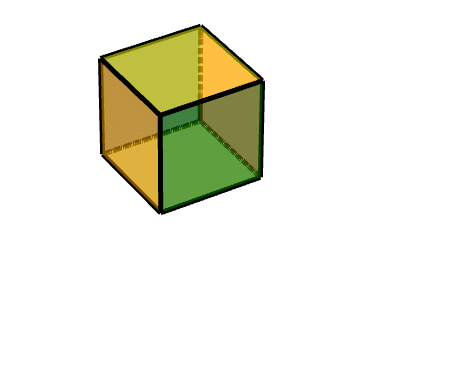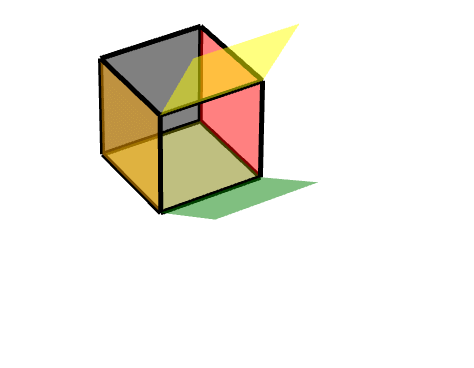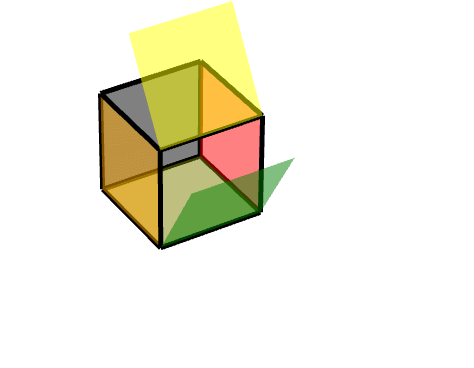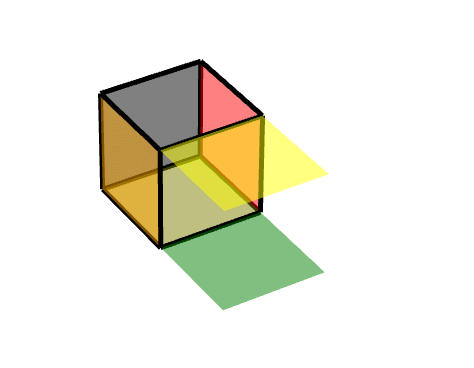
描述為,對點(11-1)進行旋轉,沿Z軸旋轉180度。
Code:
```c#
face4RotateTransform3D.CenterX = 1;
face4RotateTransform3D.CenterY = 1;
face4RotateTransform3D.CenterZ = -1;
(face4RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -180;
```
###### 2 平移旋轉:
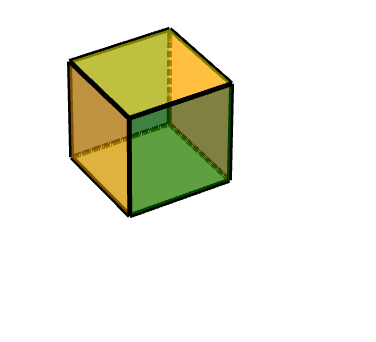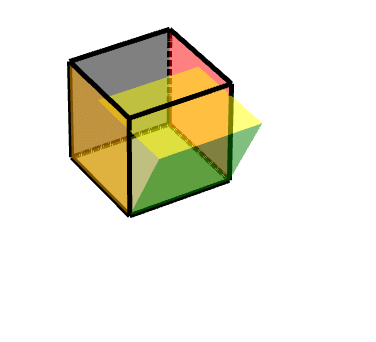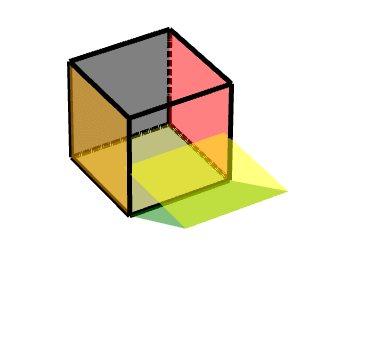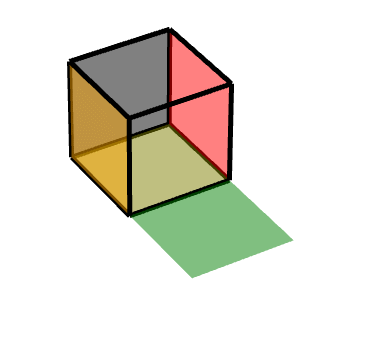
從側面看的平移軌跡:
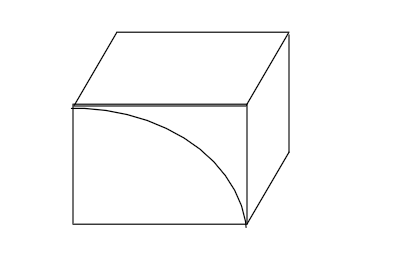
此平移按X和Y軸方向分解示意圖:
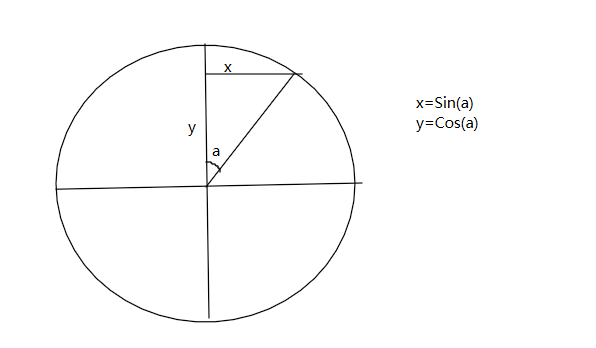
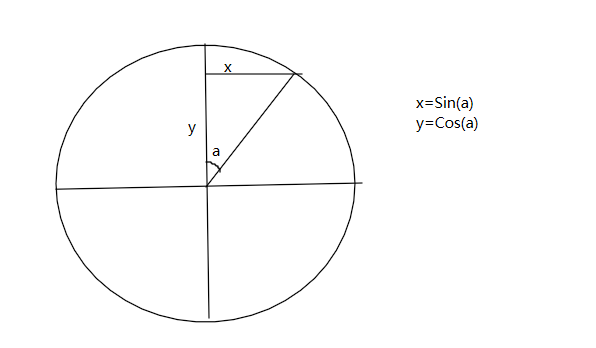
其中X方向可以描述為:
在t時間內,L為邊長
x方向值為:x=L*Sin(a)
y方向值為:y=L*Cos(a)
其中角度a可描述為:(PI/2)*currentTime/totalAnimationDuration
如果我們將動畫描述成幀動畫,綜上:
X方向平移動畫幀
```c#
LinearDoubleKeyFrame GetFace4OffsetXKeyFrame(double time)
{
return new LinearDoubleKeyFrame(borderLength * Math.Sin(time * (Math.PI / 2) / keyFrameAnimationTotalTimeM), KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
}
```
Y方向平移動畫幀
```c#
LinearDoubleKeyFrame GetFace4OffsetYKeyFrame(double time)
{
return new LinearDoubleKeyFrame(-(borderLength - borderLength * Math.Cos(time * (Math.PI / 2) / keyFrameAnimationTotalTimeM)), KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
}
```
## 3 三級旋轉面
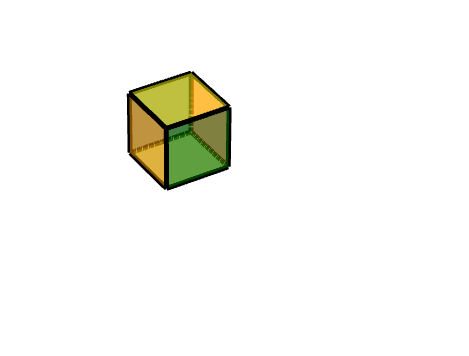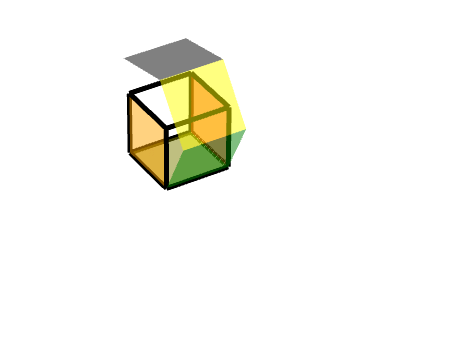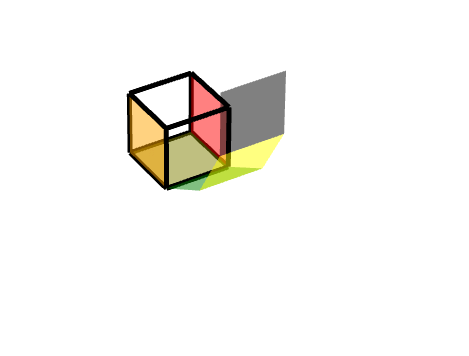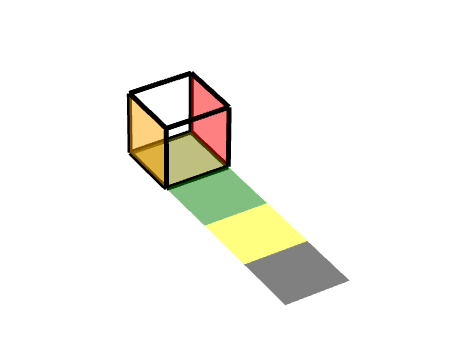
同理,我們可以把它理解為兩個旋轉的結合,**一個軸對稱旋轉+一個平移旋轉**
###### 軸對稱旋轉:

描述為,對點(-110)進行旋轉,沿Z軸旋轉270度。
Code:
```c#
face1RotateTransform3D.CenterX = -1;
face1RotateTransform3D.CenterY = 1;
face1RotateTransform3D.CenterZ = 0;
(face1RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -270;
DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));
```
###### 平移旋轉:
平移旋轉的量需要通過分解軸旋轉來得出。
通過觀察我們可以將其分為**兩個軸旋轉**,第一個旋轉是該面沿著**A軸**的軸對稱旋轉(自身旋轉),第二個是二級面的沿著**B軸**的軸對稱旋轉(相對面旋轉)
A稜邊沿著A·軌跡旋轉,B稜邊沿著B·軌跡旋轉
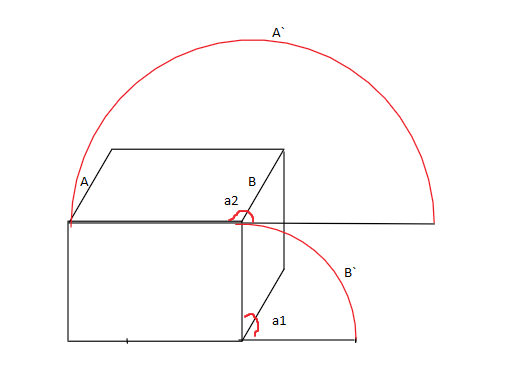
###### 則沿著B軸的旋轉,與二級面分解一樣:
###### A軸旋轉分解:
對於y,y=Sin(a2)
對於x,分為**兩種情況**:
當a2處於0-PI/2時,x=Cos(a2),
當a2處於PI/2-PI時,y=L-Cos(a2)

把上述兩個分解加一起就得到了X=xa+xb,y=ya+yb,
Code:
X
```c#
LinearDoubleKeyFrame GetFace1OffsetXKeyFrame(double time)
{
//自身邊的定位座標
double angle = time / keyFrameAnimationTotalTimeM;
double xa, xb;
double xTotal;
if (angle <= 1 / 2)
{
//0-1/2PI
xa = borderLength * Math.Cos(Math.PI * time / keyFrameAnimationTotalTimeM);
}
else
{
//1/2PI-PI
xa = borderLength - borderLength * Math.Cos(Math.PI * time / keyFrameAnimationTotalTimeM);
}
//前軸定位座標
xb = borderLength * Math.Sin((Math.PI / 2) * time / keyFrameAnimationTotalTimeM);
xTotal = xa + xb;
return new LinearDoubleKeyFrame(xTotal, KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
}
```
Y
```c#
Timeline Face1ExpandedAnimation_MoveOffsetY_UsingKeyFrames()
{
DoubleAnimationUsingKeyFrames DoubleAnimation = new DoubleAnimationUsingKeyFrames();
DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));
DoubleAnimation.Completed += ((sender, e) =>
{
faceStoryboard.Remove(tileButton);
});
Storyboard.SetTargetName(DoubleAnimation, "face1TranslateTransform3D");
Storyboard.SetTargetProperty(DoubleAnimation,
new PropertyPath(TranslateTransform3D.OffsetYProperty));
for (double i = 0; i <= keyFrameAnimationTotalTimeM + keyFrameAnimationIntervalM; i += keyFrameAnimationIntervalM)
{
DoubleAnimation.KeyFrames.Add(GetFace1OffsetYKeyFrame(i));
}
return DoubleAnimation;
}C
```
## 4 雙重軸對稱旋轉+平移旋轉面
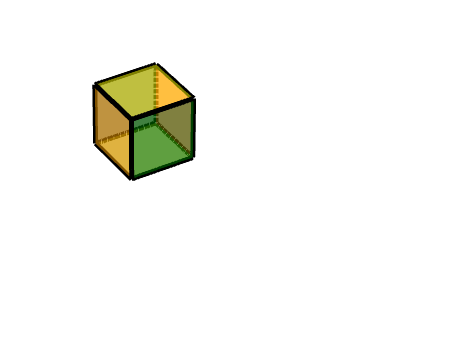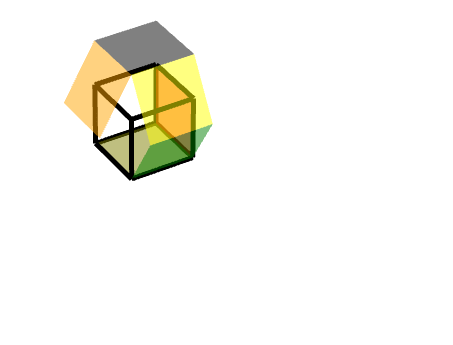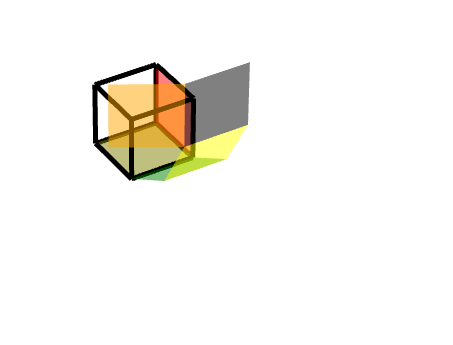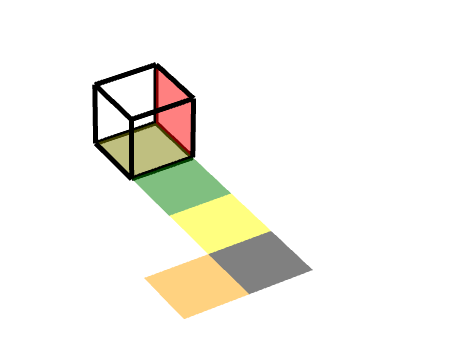
如圖所示,左邊這個橙色的面,在黑色的三級旋轉面之上又增加一個沿著Z軸的旋轉。
此時可以簡單地分解為**三級旋轉面的旋轉+沿著Z軸的旋轉**。
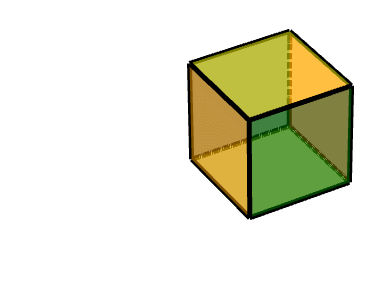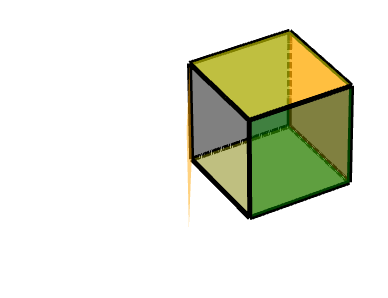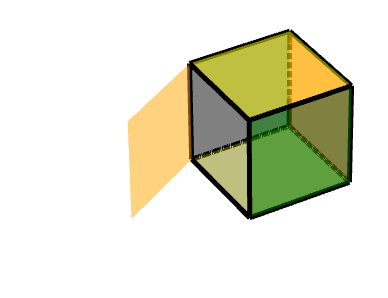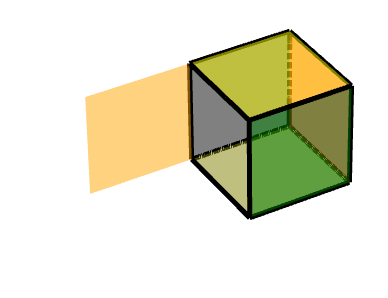
###### 三級旋轉面的旋轉:
見上文
###### Z軸旋轉
可描述為:對點(-1-11)進行旋轉,沿Z軸旋轉90度。
```
face5RotateTransform3D.CenterX = -1;
face5RotateTransform3D.CenterY = -1;
face5RotateTransform3D.CenterZ = 1;
(face5RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 1, 0);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -90;
DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM
