容斥原理（Inclusion–exclusion principle），是指在計數時，必須註意無一重復，無一遺漏，為了使重疊部分不被重復計算，人們研究出一種新的計數方法。這種方法的基本思想是：先不考慮重疊的情況，把包含於某內容中的所有對象的數目先計算出來，然後再把計數時重復計算的數目排斥出去，使得計算的結果既無遺漏又無重復，這種計數的方法稱為容斥原理。——以上來自百度百科

設S為有限集,,則

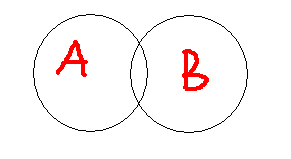
兩個集合的容斥關系公式：A∪B=A+B-A∩B(∩：重合的部分）

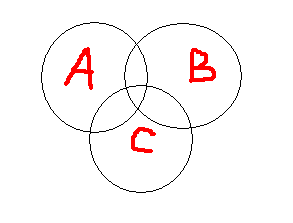
三個集合的容斥關系公式：A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C

詳細推理如下：

1、等式右邊改造={[（A+B-A∩B）+C-B∩C]-C∩A}+A∩B∩C

2、分塊標記如右圖圖：1245構成A，2356構成B，4567構成C

3、等式右邊（）裏指的是下圖的1+2+3+4+5+6六部分：

那麽A∪B∪C還缺部分7。

4、等式右邊[]號裏+C（4+5+6+7）後，相當於A∪B∪C多加了4+5+6三部分，

減去B∩C（即5+6兩部分）後，還多加了部分4。

5、等式右邊{}裏減去C∩A（即4+5兩部分）後，A∪B∪C又多減了部分5，

則加上A∩B∩C（即5）剛好是A∪B∪C。

原理 1

如果被計數的事物有A、B兩類，那麽，A類B類元素個數總和=屬於A類元素個數+屬於B類元素個數—既是A類又是B類的元素個數。（A∪B=A+B-A∩B)

原理 2

如果被計數的事物有A、B、C三類，那麽，A類和B類和C類元素個數總和=A類元素個數+B類元素個數+C類元素個數—既是A類又是B類的元素個數—既是A類又是C類的元素個數—既是B類又是C類的元素個數+既是A類又是B類而且是C類的元素個數。（A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C）

自己選的路，跪著也要走完！！！

容斥原理