摘自YYF的blog，斜率優化，敬一個！

　　P教授要去看奧運，但是他舍不下他的玩具，於是他決定把所有的玩具運到北京。他使用自己的壓縮器進行壓縮，其可以將任意物品變成一堆，再放到一種特殊的一維容器中。P教授有編號為1...N的N件玩具，第i件玩具經過壓縮後變成一維長度為Ci.為了方便整理，P教授要求在一個一維容器中的玩具編號是連續的。同時如果一個一維容器中有多個玩具，那麽兩件玩具之間要加入一個單位長度的填充物，形式地說如果將第i件玩具到第j個玩具放到一個容器中，那麽容器的長度將為 x=j-i+Sigma(Ck) i<=K<=j 制作容器的費用與容器的長度有關，根據教授研究，

Input

　　第一行輸入兩個整數N，L.接下來N行輸入Ci.1<=N<=50000,1<=L,Ci<=10^7

Output

　　輸出最小費用

Sample Input

5 4
3
4
2
1
4

Sample Output

1

　　先推出普通dp的方程

f[i] = min{f[j] + (sum[i] - sum[j] + i - j - 1 - L)²}

　　這方程明顯是O(n²)級別的，再看看這賣萌的數據範圍，不用質疑，鐵定超時。還是來考慮一下優化(例如斜率優化)吧。由於這方程長得太醜了，於是決定簡化一下

　　設S(i) = sum[i] + i，C = L + 1

　　於是方程變成了這樣

f[i] = min{f[j] + (S(i) - S（j） - C)²}

　　現在假設在狀態i之前有兩個可以轉移到i的兩個狀態j, k(j < k),現在使j比k更優，那麽它要滿足

f[j] + (S(i) - S（j） - C)² < f[k] + (S(i) - S（k） - C)²

　　看平方不爽，而且無法化簡，果斷完全平方公式拆掉

f[j] + [S(i) - (S（j） + C)]² < f[k] + [S(i) - (S（k） + C)]²

f[j] + (S(j) + C)²

　　（其實可以一起拆掉，只不過中途有些地方可以直接"抵消"）繼續"拆"括號，移項

f[j] + S(j)² + 2S(j)C - 2S(i)[S(j) - S(k)] < f[k] + S(k)² + 2S(k)C

　　繼續，右邊只留一個和i有關的單項式

(f[j] + S(j)² + 2S(j)C) - (f[k] + S(k)² + 2S(k)C) < 2S(i)[S(j) - S(k)]

　　繼續移項，右邊只留和i有關的式子

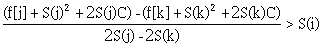
　　註意，S(i)是單調遞增，所以S(j) - S(k) < 0，移項的時候不等號方向相反，於是我們愉快地得到了斜率方程（幹什麽？斜率優化去掉一個n）。

　　對於狀態i，用(f[i] + S(i)² + 2S(i)C)作縱坐標，2S(i)作橫坐標，刪掉上凸點，維護一條斜率遞增的折線即可。

bzoj 1010 玩具裝箱toy