NOIP 華容道
描述
小 B 最近迷上了華容道,可是他總是要花很長的時間才能完成一次。於是,他想到用編程來完成華容道:給定一種局面,華容道是否根本就無法完成,如果能完成,最少需要多少時間。
小 B 玩的華容道與經典的華容道遊戲略有不同,遊戲規則是這樣的:
-
在一個 n*m 棋盤上有 n*m 個格子,其中有且只有一個格子是空白的,其余 n*m-1個格子上每個格子上有一個棋子,每個棋子的大小都是 1*1 的;
-
有些棋子是固定的,有些棋子則是可以移動的;
-
任何與空白的格子相鄰(有公共的邊)的格子上的棋子都可以移動到空白格子上。 遊戲的目的是把某個指定位置可以活動的棋子移動到目標位置。
給定一個棋盤,遊戲可以玩 q 次,當然,每次棋盤上固定的格子是不會變的,但是棋盤上空白的格子的初始位置、指定的可移動的棋子的初始位置和目標位置卻可能不同。第 i 次玩的時候,空白的格子在第 EX_iEX?i?? 行第 EY_iEY?i?? 列,指定的可移動棋子的初始位置為第 SX_iSX?i?? 行第 SY_iSY?i?? 列,目標位置為第 TX_iTX?i?? 行第 TY_iTY?i?? 列。
假設小 B 每秒鐘能進行一次移動棋子的操作,而其他操作的時間都可以忽略不計。請你告訴小 B 每一次遊戲所需要的最少時間,或者告訴他不可能完成遊戲。
格式
輸入格式
第一行有 3 個整數,每兩個整數之間用一個空格隔開,依次表示 n、m 和 q;
接下來的 n 行描述一個 n*m 的棋盤,每行有 m 個整數,每兩個整數之間用一個空格隔開,每個整數描述棋盤上一個格子的狀態,0 表示該格子上的棋子是固定的,1 表示該格子上的棋子可以移動或者該格子是空白的。
接下來的 q 行,每行包含 6 個整數依次是 EX_iEX?i??、EY_iEY?i??、SX_iSX?i??、SY_iSY?i??、TX_iTX?i??、TY_iTY?i??,每兩個整數之間用一個空格隔開,表示每次遊戲空白格子的位置,指定棋子的初始位置和目標位置。
輸出格式
輸出有 q 行,每行包含 1 個整數,表示每次遊戲所需要的最少時間,如果某次遊戲無法完成目標則輸出−1。
樣例1
樣例輸入1
3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2
樣例輸出1
2
-1
限制
每個測試點1s。
提示
###樣例說明
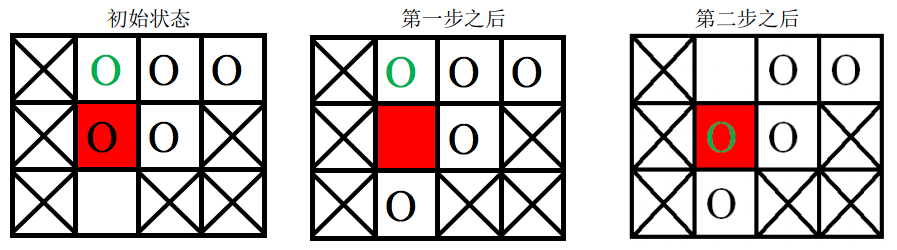
棋盤上劃叉的格子是固定的,紅色格子是目標位置,圓圈表示棋子,其中綠色圓圈表示目標棋子。
-
第一次遊戲,空白格子的初始位置是 (3, 2)(圖中空白所示),遊戲的目標是將初始位置在(1, 2)上的棋子(圖中綠色圓圈所代表的棋子)移動到目標位置(2, 2)(圖中紅色的格子)上。
移動過程如下:
-
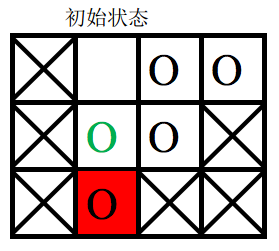
第二次遊戲,空白格子的初始位置是(1, 2)(圖中空白所示),遊戲的目標是將初始位置在(2, 2)上的棋子(圖中綠色圓圈所示)移動到目標位置 (3, 2)上。
要將指定塊移入目標位置,必須先將空白塊移入目標位置,空白塊要移動到目標位置,必然是從位置(2,2)上與當前圖中目標位置上的棋子交換位置,之後能與空白塊交換位置的只有當前圖中目標位置上的那個棋子,因此目標棋子永遠無法走到它的目標位置,遊戲無法完成。
###數據範圍
對於 30%的數據,1 ≤ n, m ≤ 10,q = 1;
對於 60%的數據,1 ≤ n, m ≤ 30,q ≤ 10;
對於 100%的數據,1 ≤ n, m ≤ 30,q ≤ 500。
來源
NOIP 2013 提高組 day 2
首先可以考慮全盤爆搜,讓空白方塊到處亂跑,狀態要記錄空白方塊的位置和目標棋子的位置,所以狀態總數為n2m2,時間復雜度為O(n2m2q).
然後來想想優化,當空白方塊跑到目標棋子周圍時,再到處瞎跑沒什麽意義而且多個詢問棋盤不會改變,所以呢,可以考慮預處理一下當目標棋子的位置為(i, j)時,空白方塊在目標棋子a方向時移到b方向最少要的步數。花費一個O(n2m2)的時間去跑nm次bfs。
這有什麽用呢?我們先把空白棋子移到目標棋子周圍然後就可以跑spfa了,spfa除了記錄目標棋子的位置再記錄一下空白棋子在哪個方向,轉移的時候方向相反,這個距離就可以用之前預處理的結果了。這樣總時間復雜度為O(n2m2 + qn2 + kqn2),其中k為spfa的常數。
Code
1 #include<iostream> 2 #include<fstream> 3 #include<sstream> 4 #include<string> 5 #include<cstdio> 6 #include<cstdlib> 7 #include<cstring> 8 #include<ctime> 9 #include<cmath> 10 #include<algorithm> 11 #include<cctype> 12 #include<vector> 13 #include<stack> 14 #include<set> 15 #include<map> 16 #include<queue> 17 #ifndef WIN32 18 #define Auto "%lld" 19 #else 20 #define Auto "%I64d" 21 #endif 22 using namespace std; 23 typedef bool boolean; 24 #define inf 0x3fffffff 25 #define smin(a, b) (a) = min((a), (b)) 26 #define smax(a, b) (a) = max((a), (b)) 27 28 template<typename T> 29 class Matrix { 30 public: 31 T* p; 32 int col, line; 33 Matrix():p(NULL), col(0), line(0) { } 34 Matrix(int line, int col):line(line), col(col) { 35 p = new T[(const int)(line * col)]; 36 } 37 38 T* operator [] (int pos) { 39 return p + pos * col; 40 } 41 }; 42 43 typedef class Point { 44 public: 45 int x; 46 int y; 47 Point(int x = 0, int y = 0):x(x), y(y) { } 48 }Point; 49 50 ifstream fin("puzzle.in"); 51 ofstream fout("puzzle.out"); 52 53 int n, m, q; 54 Matrix<boolean> walkable; 55 int dis[35][35][4][4]; 56 57 inline void init() { 58 fin >> n >> m >> q; 59 walkable = Matrix<boolean>(n, m); 60 for(int i = 0; i < n; i++) 61 for(int j = 0, x; j < m; j++) { 62 fin >> x; 63 if(x) walkable[i][j] = true; 64 else walkable[i][j] = false; 65 } 66 } 67 68 const int mov[2][4] = {{1, -1, 0, 0}, {0, 0, 1, -1}}; 69 70 boolean exceeded(int x, int y) { 71 if(x < 0 || x >= n) return true; 72 if(y < 0 || y >= m) return true; 73 return false; 74 } 75 76 int dep[35][35][35][35]; 77 queue<Point> que; 78 queue<Point> que1; 79 80 boolean vis1[35][35]; 81 int dep1[35][35]; 82 inline int bfs1(Point s, Point t, Point g) { 83 if(s.x == t.x && s.y == t.y) return 0; 84 memset(vis1, false, sizeof(vis1)); 85 dep1[s.x][s.y] = 0; 86 vis1[s.x][s.y] = true; 87 que.push(s); 88 while(!que.empty()) { 89 Point e = que.front(); 90 que.pop(); 91 for(int i = 0; i < 4; i++) { 92 Point eu(e.x + mov[0][i], e.y + mov[1][i]); 93 if(exceeded(eu.x, eu.y)) continue; 94 if(!walkable[eu.x][eu.y]) continue; 95 if(vis1[eu.x][eu.y]) continue; 96 if(eu.x == g.x && eu.y == g.y) continue; 97 dep1[eu.x][eu.y] = dep1[e.x][e.y] + 1; 98 if(eu.x == t.x && eu.y == t.y) { 99 while(!que.empty()) que.pop(); 100 return dep1[eu.x][eu.y]; 101 } 102 vis1[eu.x][eu.y] = true; 103 que.push(eu); 104 } 105 } 106 return -1; 107 } 108 109 inline void init_dis() { 110 for(int i = 0; i < n; i++) 111 for(int j = 0; j < m; j++) 112 for(int p = 0; p < 4; p++) { 113 Point w(i + mov[0][p], j + mov[1][p]); 114 for(int q = 0; q < 4; q++) { 115 Point t(i + mov[0][q], j + mov[1][q]); 116 if(exceeded(w.x, w.y) || exceeded(t.x, t.y)) dis[i][j][p][q] = -1; 117 else if(!walkable[w.x][w.y] || !walkable[i][j] || !walkable[t.x][t.y]) dis[i][j][p][q] = -1; 118 else if(p == q) dis[i][j][p][q] = 0; 119 else dis[i][j][p][q] = bfs1(w, t, Point(i, j)); 120 } 121 } 122 } 123 124 boolean vis2[4][35][35]; 125 int f[4][35][35]; 126 queue<int> que2; 127 inline int spfa(Point s, Point t, Point w) { 128 memset(vis2, false, sizeof(vis2)); 129 memset(f, 0x7f, sizeof(f)); 130 for(int i = 0; i < 4; i++) { 131 Point e(s.x + mov[0][i], s.y + mov[1][i]); 132 if(exceeded(e.x, e.y)) continue; 133 if(!walkable[e.x][e.y]) continue; 134 f[i][s.x][s.y] = bfs1(Point(w.x, w.y), e, Point(s.x, s.y)); 135 if(f[i][s.x][s.y] == -1) f[i][s.x][s.y] = 0x7f7f7f7f; 136 } 137 for(int i = 0; i < 4; i++) { 138 que.push(s); 139 que2.push(i); 140 } 141 while(!que.empty()) { 142 Point e = que.front(); 143 int ed = que2.front(); 144 que.pop(); 145 que2.pop(); 146 vis2[ed][e.x][e.y] = false; 147 for(int i = 0; i < 4; i++) { 148 Point eu(e.x + mov[0][i], e.y + mov[1][i]); 149 int eud = i ^ 1; 150 if(exceeded(eu.x, eu.y)) continue; 151 if(!walkable[eu.x][eu.y]) continue; 152 if(dis[e.x][e.y][ed][i] == -1) continue; 153 if(f[ed][e.x][e.y] + dis[e.x][e.y][ed][i] + 1 < f[eud][eu.x][eu.y]) { 154 f[eud][eu.x][eu.y] = f[ed][e.x][e.y] + dis[e.x][e.y][ed][i] + 1; 155 if(!vis2[eud][eu.x][eu.y]) { 156 vis2[eud][eu.x][eu.y] = true; 157 que.push(eu); 158 que2.push(eud); 159 } 160 } 161 } 162 } 163 int ret = inf; 164 for(int i = 0; i < 4; i++) 165 smin(ret, f[i][t.x][t.y]); 166 if(ret == inf) return -1; 167 return ret; 168 } 169 170 int res = inf; 171 inline void solve() { 172 int wx, wy, sx, sy, tx, ty; 173 while(q--) { 174 res = inf; 175 fin >> wx >> wy >> sx >> sy >> tx >> ty; 176 wx--, wy--, sx--, sy--, tx--, ty--; 177 if(sx == tx && sy == ty) { 178 fout << "0" << endl; 179 continue; 180 } 181 fout << spfa(Point(sx, sy), Point(tx, ty), Point(wx, wy)) << endl; 182 } 183 } 184 185 int main() { 186 init(); 187 init_dis(); 188 solve(); 189 return 0; 190 }
NOIP 華容道