強連通：在有向圖G中，兩個頂點間至少存在一條路徑，則兩個點強連通。

強連通圖：在有向圖中，每兩個頂點都強連通，則有向圖G就是一個強連通圖。

強連通分量：在非強連通圖中的極大強連通子圖，就稱為強連通分量。

直接根據定義，可以通過雙向遍歷取交集的方法求強連通分量，但是其復雜度為O(N^2+M)。更好的方法是用tarjan算法，其時間復雜度為O(N+M)。

tarjan:其實就是對圖的深度優先遍歷。

算法模擬：

定義 DFN [u]為節點u被搜索到時的次序編號（也就是所遍歷的第幾個）；

定義LOW[U]為U或者U 的子數能夠追溯到最早的棧中節點的次序號。

　　（當DFN[U] == LOE[U] 時，以U為根的搜索子樹上所有節點是一個強連通分量。實質上就是這個點的整個子樹回溯完了，沒有鏈接的路了）

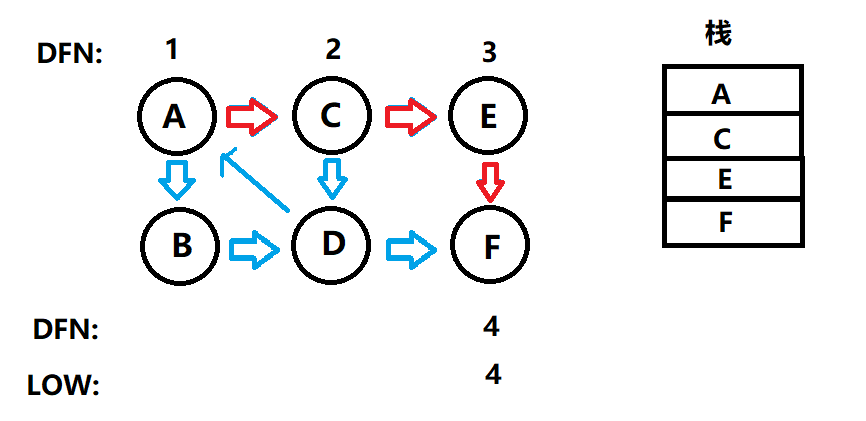
此時的F點DNF[F]==LOW[F]=4，所以F為一個強連通分量，只有它自己本身。

然後返回節點E，此時發現 DFN[E] == LOW[E] =5,所以E也單獨為一個強連通分量，只有他本身。

然後返回節點C:

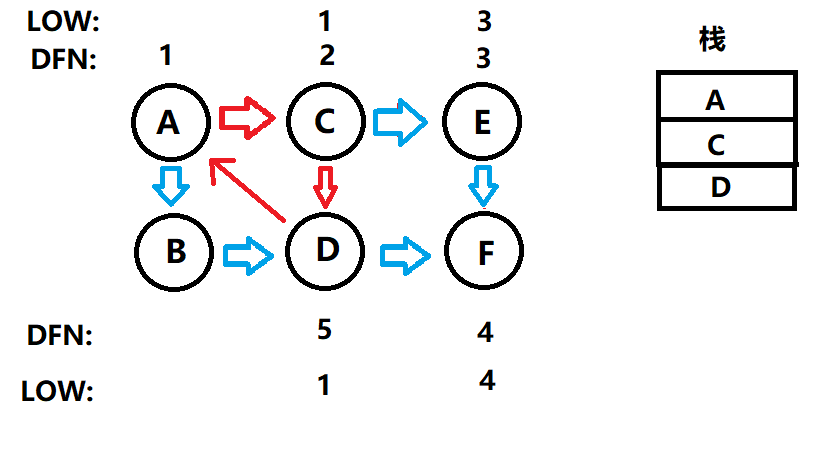
從C節點繼續搜其他的C的子樹，搜到節點D,將D加入棧中。然後D有 D -> F ，但是F 已經出棧，所以F節點直接跳過，

還有一個節點A ， 但是呢，A節點已經在棧中，所以LOW[D] = DFN[A] = 1,然後是一個回溯的過程，所以呢，LOW[C] = LOW [D] =1;

所以說明這三個節點已經是一個強連通分量了。

繼續回到節點A,最後訪問B節點，，然後 B-> D ，然而 D點還在棧中，所以LOW[B] = DFN [ D ] = 5 ,DFN[B] = 6 ;

沒有其他點了，算法結束，最後得到 {A,B,C,D} ，{E}, {F}為強連通分量。

在tarjan算法中，每個點只被訪問了一次，而且只進行了一次的棧，每條邊也只被訪問了一次，。所以該算法的時間復雜度為O(N+M);

程序模板：

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <iostream>
  4 using namespace std;
  5 
  6 #define N 100
  7 #define M 100
  8 
  9 struct node
 10 {
 11     int
 
 v;
 12     int next;
 13 };
 14 
 15 node edge[M];//邊的集合
 16 
 17 int a[N];//頂點的集合
 18 int instack[N];//模擬棧，標記是否在棧中
 19 int stack[N];
 20 int belong[N];//各個頂點屬於哪個強連通分量
 21 int DFN[N];
 22 int LOW[N];//棧中能夠追溯到最早的節點序號
 23 int n;//點的個數
 24 int m;//邊的個數
 25 int count;//邊的計數器
 26 int index;//序號（時間戳）
 27 int top;
 28 int sun;//強連通分量的個數
 29 
 30 //用鄰接表存儲 
 31 void add_edge(int u,int v)
 32 {
 33     edge[count].next=a[u];
 34     edge[count].v=v;
 35     a[u]=count++;
 36 } 
 37 
 38 void tarjan(int u)
 39 {
 40     int i,j;
 41     int v;
 42     DFN[u]=LOW[u]=++index;
 43     instack[u]=true;
 44     stack[++top]=u;//進棧 
 45     for(i=a[u];i!=-1;i=edge[i].next)
 46     {
 47         v=edge[i].v;
 48         if(!DFN[v])//如果DFN[v]為0，沒被訪問 
 49         {
 50             tarjan(v);
 51             //一個回溯的過程 
 52             if(LOW[v]<LOW[u])
 53                 LOW[u]=LOW[v];
 54         }
 55         else
 56         {
 57             if(instack[v]&&DFN[v]<LOW[u])
 58                 LOW[u]=DFN[v];
 59         }
 60     }
 61     if(DFN[u]==LOW[u])
 62     {
 63         sun++;
 64         //出棧 
 65         do
 66         {
 67             j=stack[top--];
 68             instack[j]=false;
 69             belong[j]=sun;
 70         }while(j!=u);
 71         
 72     }
 73 }
 74 
 75 void solve()
 76 {
 77     int i;
 78     top=index=sun=0;
 79     memset(DFN,0,sizeof(DFN));
 80     memset(LOW,0,sizeof(LOW));
 81     for(i=1;i<=n;i++)
 82     {
 83         if(!DFN[i])
 84             tarjan(i);
 85     }
 86 }
 87 
 88 int main()
 89 {
 90     int i,j,k;
 91     count=0;
 92     memset(a,-1,sizeof(a));
 93     scanf("%d %d",&n,&m);
 94     for(i=1;i<=m;i++)
 95     {
 96         scanf("%d %d",&j,&k);
 97         add_edge(j,k);
 98     }
 99     solve();
100     for(i=1;i<=n;i++)
101         printf("%d ",belong[i]);
102 }

tarjan有向圖的強連通