在處理類似下面的問題中，一般的計數方法會出現問題：假如你要用紅、藍兩種顏色給一個正四面體的四個頂點著色，試問存在多少種不同的著色方案？

在高中我們常用的方法是模擬塗色過程，分情況討論，然後基於分步乘法原理。但是在那裏沒有考慮幾何體通過旋轉等操作帶來的對稱性，在本文中，我們就來介紹一種專門處理這類問題的工具——Polya計數。

首先我們要做的是引入一些基本的概念。

置換：

關於置換更多的細節我們在《抽象代數基礎教程》中繼續討論，這裏我們只需簡單的了解其概念即可。

關於置換還需要了解的就是它的合乘運算。

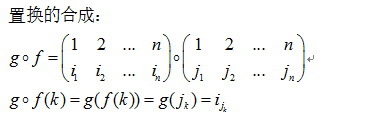
置換這個工具可以方便我們符號化圖形的對稱分析過程，下面給出要給非常簡單的例子，以幫助理解置換如何描述幾何體的對稱。

考察如下的正方形。

(一個正方形，四個頂點為1234)

我們需要去思考，如何利用置換來描述那些運動，使得正方形位置沒變(但是對應標號的頂點可能發生了移動)。

容易看到符合要求的運動有兩類。

1) 將正方形繞中心旋轉(取順時針即可)0°、90°、180°、270°.

2) 將正方形按照兩條對角線和兩條對邊中點連線，立體得翻轉180°。

那麽我們可以發現運動前的正方形頂點序號和運動後的，其實就形成了一個置換。

此時我們開始給出染色方案的數學描述。

基於以上的鋪墊，我們可以給出Burnside引理，用於給出一個計數非等價著色數的公式。

在給出Burnside定理之後，我們下面結合幾個簡單的題目，來加強對這個定理的理解。

問題到這裏，就得到很大的改觀，之前我們需要基於置換群和著色集合，進行遍歷考察來計算Burnside定理和式的一般項，而現在我們只需要，分析置換群G中的每個置換，然後結合顏色數，就可以進行計算了。

我們還需要進一步努力，因為從定理4可以看到，我們用k種顏色形成著色集合，是沒有顯示顏色的出現次數的，而如果規定某種顏色的出現的次數，我們應該如何處理呢？

最後我們給出立方體的非等價的染色分析，在一般帶的考察polya的題目中容易考察但是其對稱群較為繁冗容易出錯，因此最好一次分析之後記住結論。

例子(立方體的頂點與面的著色)：

用制定數量的顏色對立方體的頂點和面進行著色，嘗試求立方體的對稱群和非等價的著色方案數目。

考察立方體的對稱操作，它們一共可分為如下的四種類型共24種對稱：

(1) 恒等對稱1個。

(2) 固定一對對立面進行旋轉：

(a)90°

(b)180°

(c)270°

由於共有三對對立面，所以上面各有3個共9個。

(3) 繞一對對邊重點連線旋轉180°，由於有6對，這裏有6個對稱。

(4) 繞對頂點進行旋轉：

(a)120°

(b)240°

可以看到一個立方體的對稱群友24個置換，下面我們只需要考察每個置換f的type(f)，以期得到立方體的非等價染色的生成函數。

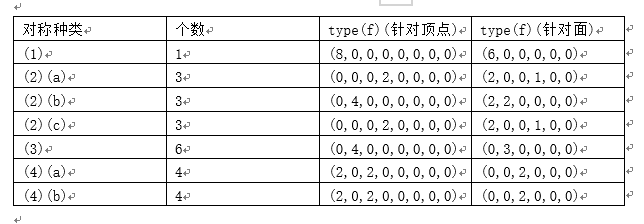
同理我們可以對面對稱群進行完全一樣的討論，結果如下：

組合數學及其應用——polya計數