一.kmeans聚類：

基本方法流程

1.首先隨機初始化k個中心點

2.將每個實例分配到與其最近的中心點，開成k個類

3.更新中心點，計算每個類的平均中心點

4.直到中心點不再變化或變化不大或達到叠代次數

優缺點：該方法簡單，執行速度較快。但其對於離群點處理不是很好，這是可以去除離群點。kmeans聚類的主要缺點是隨機的k個初始中心點的選擇不夠嚴謹，因為是隨機，所以會導致聚類結果準確度不穩定。

二.kmeans++聚類：

kmeans++方法是針對kmeans的主要缺點進行改進，通過在初始中心點的選擇上改進不足。

中心點的選擇：

1.首先隨機選擇一個中心點

2.計算每個點到與其最近的中心點的距離為dist，以正比於dist的概率，隨機選擇一個點作為中心點加入中心點集中，重復直到選定k個中心點

3.計算同kmeans方法

三.評估方法

誤差平方和可以評估每次初始中心點選擇聚類的優劣，公式如下：

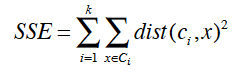
計算每個點到它自己的類的中心點的距離的平方和，外層是不同類間的和。根據每次初始點的選擇聚類結果計算SSE，SSE值越小結果越好。

四.代碼

  1 #!/usr/bin/python
  2 # -*- coding: utf-8 -*-
  3 import math
  4 import codecs
  5 import random
  6 
  7 #k-means和k-means++聚類，第一列是label標簽，其它列是數值型數據
  8 class KMeans:
  9 
 10
 
     #一列的中位數
 11     def getColMedian(self,colList):
 12         tmp = list(colList)
 13         tmp.sort()
 14         alen = len(tmp)
 15         if alen % 2 == 1:
 16             return tmp[alen // 2]
 17         else:
 18             return (tmp[alen // 2] + tmp[(alen // 2) - 1]) / 2
 19 
 20     #對數值型數據進行歸一化，使用絕對標準分[絕對標準差->asd=sum(x-u)/len(x),x的標準分->(x-u)/絕對標準差，u是中位數]
 

 21     def colNormalize(self,colList):
 22         median = self.getColMedian(colList)
 23         asd = sum([abs(x - median) for x in colList]) / len(colList)
 24         result = [(x - median) / asd for x in colList]
 25         return result
 26 
 27     ‘‘‘
 28     1.讀數據
 29     2.按列讀取
 30     3.歸一化數值型數據
 31     4.隨機選擇k個初始化中心點
 32     5.對數據離中心點距離進行分配
 33     ‘‘‘
 34     def __init__(self,filePath,k):
 35         self.data={}#原始數據
 36         self.k=k#聚類個數
 37         self.iterationNumber=0#叠代次數
 38         #用於跟蹤在一次叠代改變的點
 39         self.pointsChanged=0
 40         #誤差平方和
 41         self.SSE=0
 42         line_1=True
 43         with codecs.open(filePath,‘r‘,‘utf-8‘) as f:
 44             for line in f:
 45                 # 第一行為描述信息
 46                 if line_1:
 47                     line_1=False
 48                     header=line.split(‘,‘)
 49                     self.cols=len(header)
 50                     self.data=[[] for i in range(self.cols)]
 51                 else:
 52                     instances=line.split(‘,‘)
 53                     column_0=True
 54                     for ins in range(self.cols):
 55                         if column_0:
 56                             self.data[ins].append(instances[ins])# 0列數據
 57                             column_0=False
 58                         else:
 59                             self.data[ins].append(float(instances[ins]))# 數值列
 60         self.dataSize=len(self.data[1])#多少實例
 61         self.memberOf=[-1 for x in range(self.dataSize)]
 62 
 63         #歸一化數值列
 64         for i in range(1,self.cols):
 65             self.data[i]=self.colNormalize(self.data[i])
 66 
 67         #隨機從數據中選擇k個初始化中心點
 68         random.seed()
 69         #1.下面是kmeans隨機選擇k個中心點
 70         #self.centroids=[[self.data[i][r] for i in range(1,self.cols)]
 71         #                for r in random.sample(range(self.dataSize),self.k)]
 72         #2.下面是kmeans++選擇K個中心點
 73         self.selectInitialCenter()
 74 
 75         self.assignPointsToCluster()
 76 
 77     #離中心點距離分配點，返回這個點屬於某個類別的類型
 78     def assignPointToCluster(self,i):
 79         min=10000
 80         clusterNum=-1
 81         for centroid in range(self.k):
 82             dist=self.distance(i,centroid)
 83             if dist<min:
 84                 min=dist
 85                 clusterNum=centroid
 86         #跟蹤改變的點
 87         if clusterNum!=self.memberOf[i]:
 88             self.pointsChanged+=1
 89         #誤差平方和
 90         self.SSE+=min**2
 91         return clusterNum
 92 
 93 
 94     #將每個點分配到一個中心點，memberOf=[0,1,0,0,...]，0和1是兩個類別，每個實例屬於的類別
 95     def assignPointsToCluster(self):
 96         self.pointsChanged=0
 97         self.SSE=0
 98         self.memberOf=[self.assignPointToCluster(i) for i in range(self.dataSize)]
 99 
100     # 歐氏距離,d(x,y)=math.sqrt(sum((x-y)*(x-y)))
101     def distance(self,i,j):
102         sumSquares=0
103         for k in range(1,self.cols):
104             sumSquares+=(self.data[k][i]-self.centroids[j][k-1])**2
105         return math.sqrt(sumSquares)
106 
107     #利用類中的數據點更新中心點，利用每個類中的所有點的均值
108     def updateCenter(self):
109         members=[self.memberOf.count(i) for i in range(len(self.centroids))]#得到每個類別中的實例個數
110         self.centroids=[
111             [sum([self.data[k][i] for i in range(self.dataSize)
112                   if self.memberOf[i]==centroid])/members[centroid]
113              for k in range(1,self.cols)]
114             for centroid in range(len(self.centroids))]
115 
116     ‘‘‘叠代更新中心點（使用每個類中的點的平均坐標），
117     然後重新分配所有點到新的中心點，直到類中成員改變的點小於1%(只有不到1%的點從一個類移到另一類中)
118     ‘‘‘
119     def cluster(self):
120         done=False
121         while not done:
122             self.iterationNumber+=1#叠代次數
123             self.updateCenter()
124             self.assignPointsToCluster()
125             #少於1%的改變點，結束
126             if float(self.pointsChanged)/len(self.memberOf)<0.01:
127                 done=True
128         print("誤差平方和（SSE）: %f" % self.SSE)
129 
130     #打印結果
131     def printResults(self):
132         for centroid in range(len(self.centroids)):
133             print(‘\n\nCategory %i\n=========‘ % centroid)
134             for name in [self.data[0][i] for i in range(self.dataSize)
135                 if self.memberOf[i]==centroid]:
136                 print(name)
137 
138     #kmeans++方法與kmeans方法的區別就是初始化中心點的不同
139     def selectInitialCenter(self):
140         centroids=[]
141         total=0
142         #首先隨機選一個中心點
143         firstCenter=random.choice(range(self.dataSize))
144         centroids.append(firstCenter)
145         #選擇其它中心點，對於每個點找出離它最近的那個中心點的距離
146         for i in range(0,self.k-1):
147             weights=[self.distancePointToClosestCenter(x,centroids)
148                      for x in range(self.dataSize)]
149             total=sum(weights)
150             #歸一化0到1之間
151             weights=[x/total for x in weights]
152 
153             num=random.random()
154             total=0
155             x=-1
156             while total<num:
157                 x+=1
158                 total+=weights[x]
159             centroids.append(x)
160         self.centroids=[[self.data[i][r] for i in range(1,self.cols)] for r in centroids]
161 
162     def distancePointToClosestCenter(self,x,center):
163         result=self.eDistance(x,center[0])
164         for centroid in center[1:]:
165             distance=self.eDistance(x,centroid)
166             if distance<result:
167                 result=distance
168         return result
169 
170     #計算點i到中心點j的距離
171     def eDistance(self,i,j):
172         sumSquares=0
173         for k in range(1,self.cols):
174             sumSquares+=(self.data[k][i]-self.data[k][j])**2
175         return  math.sqrt(sumSquares)
176 
177 if __name__==‘__main__‘:
178     kmeans=KMeans(‘filePath‘,3)
179     kmeans.cluster()
180     kmeans.printResults()

kmeans與kmeans++的python實現