神經網路中BP演算法的原理與用Python實現原始碼
(1)什麼是梯度下降和鏈式求導法則
1.梯度下降
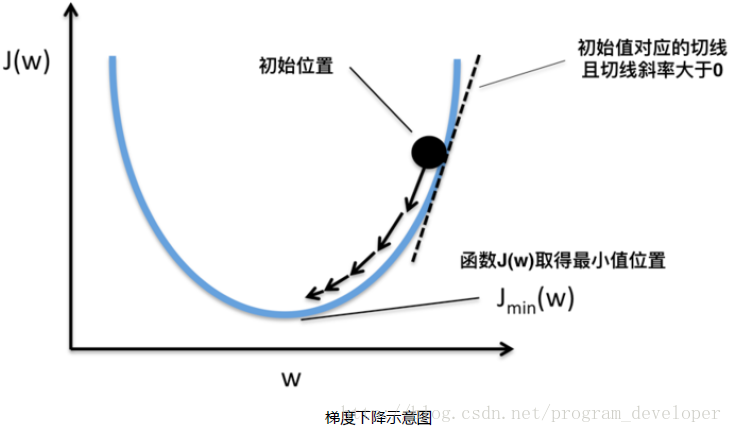
假設我們有一個函式J(w),如下圖所示。
現在,我們要求當w等於什麼的時候,J(w)能夠取到最小值。從圖中我們知道最小值在初始位置的左邊,也就意味著如果想要使J(w)最小,w的值需要減小。而初始位置的切線斜率a>0(也是該位置對應的導數大於0),w=w-eta*a(eta是學習率)就能讓w的值減小,迴圈求導更新w直到J(w)取到最小值。如果函式J(w)包含多個變數,那麼就要分別對不同的變數求偏導來更新不同變數的值。(這裡的梯度下降沒有詳細解釋,需要深入理解的同學自行查閱資料)
2.鏈式求導法則

舉個例子: 我們經常用到的啟用函式是sigmoid函式,那我們就拿這個函式來求導數。

(2)BP演算法的詳細介紹
參見《機器學習》周志華著,課本上的P101頁-P104頁,講的很詳細,仔細看看,公式推導一下,理解的很清楚。(3)用一個例子全面理解BP演算法
為了方便起見,這裡定義了三層網路,輸入層(第0層),隱藏層(第1層),輸出層(第二層)。並且每個結點沒有偏置(有偏置原理完全一樣),啟用函式為sigmod函式(不同的啟用函式,求導不同),符號和網路結構說明如下: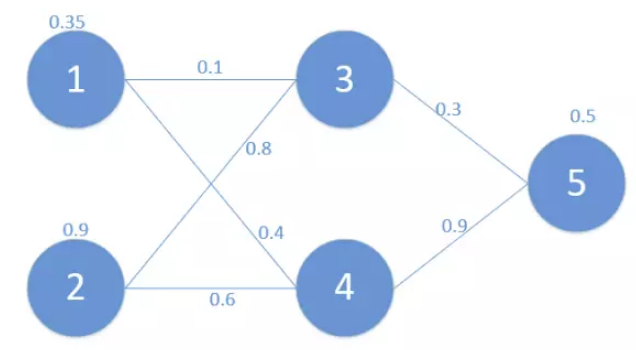
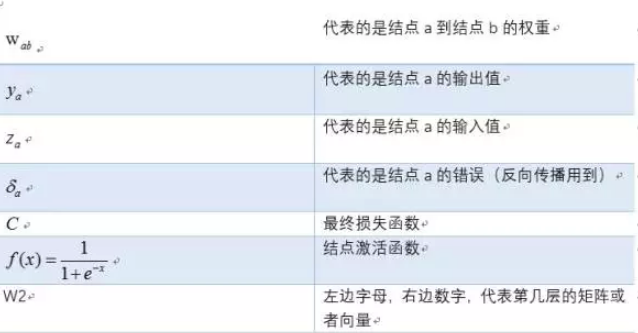
其中對應的矩陣表示如下:
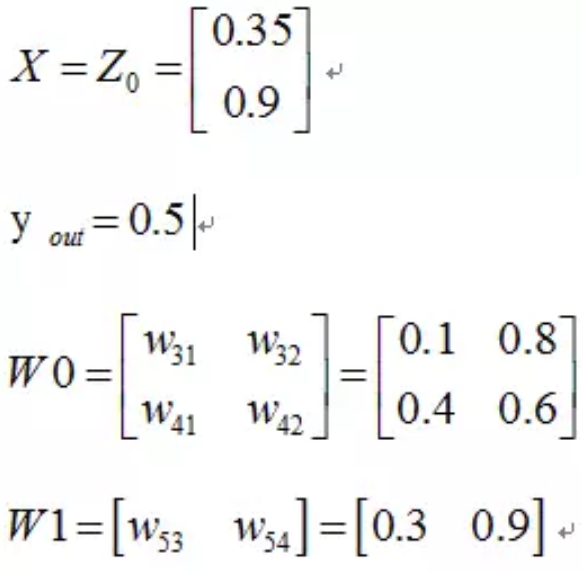
首先,我們先走一遍正向傳播,公式與相應的資料對應如下:
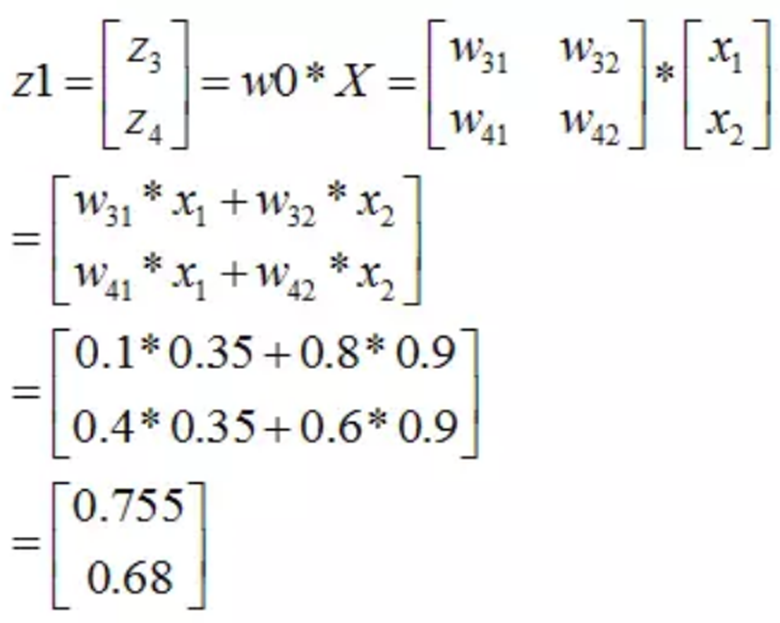 那麼第一層輸出:
那麼第一層輸出:
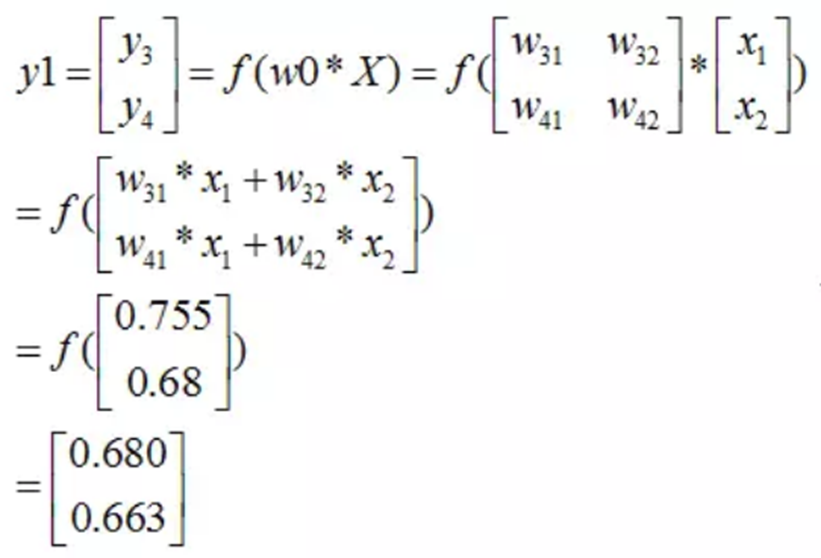
同理可以得到第二層的輸入和輸出:
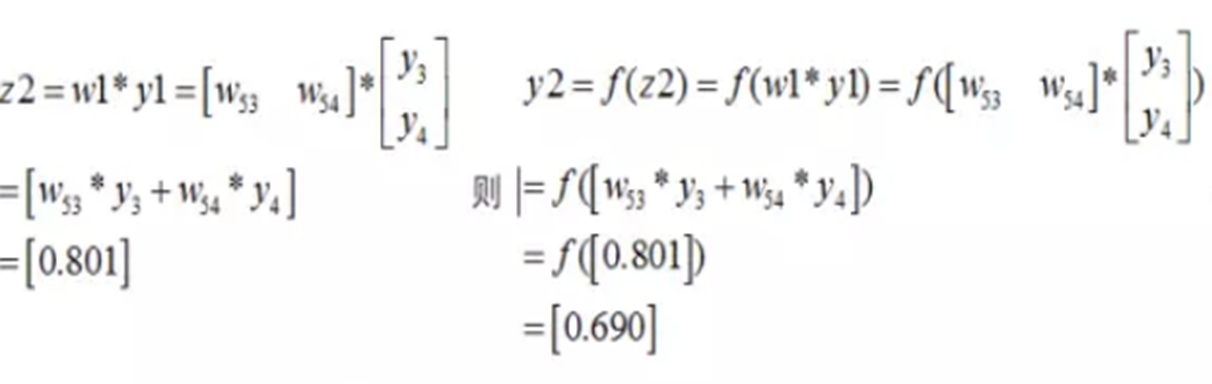
最終的損失為:
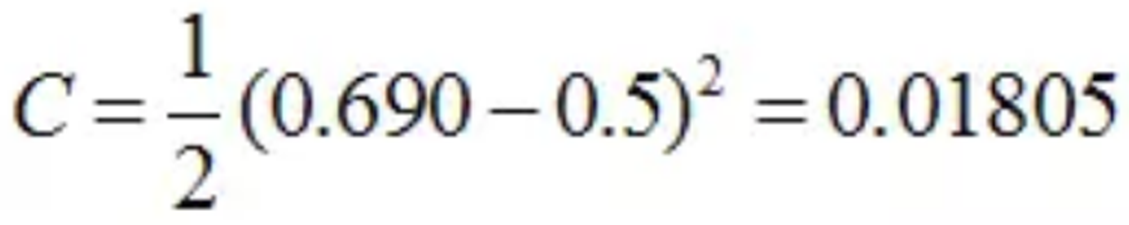
我們當然是希望這個值越小越好。這也是我們為什麼要進行訓練,調節引數,使得最終的損失最小。這就用到了我們的反向傳播演算法。
下面我們看如何反向傳播
根據公式,我們有:
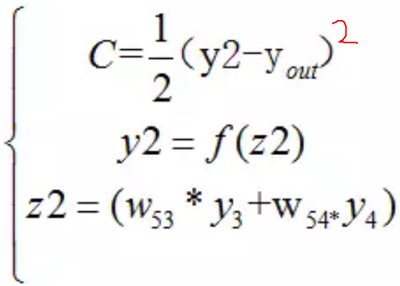
這個時候,我們需要求出C對w的偏導,則根據鏈式法則有:
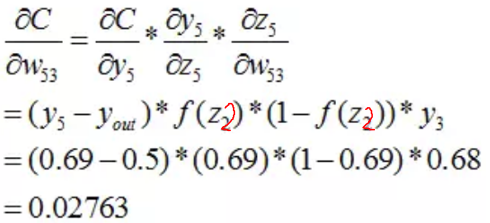
(在這裡我們可以看到不同啟用函式求導是不同的,所謂的梯度消失,梯度爆炸如果瞭解bp演算法的原理,也是非常容易理解的!)
同理W54:
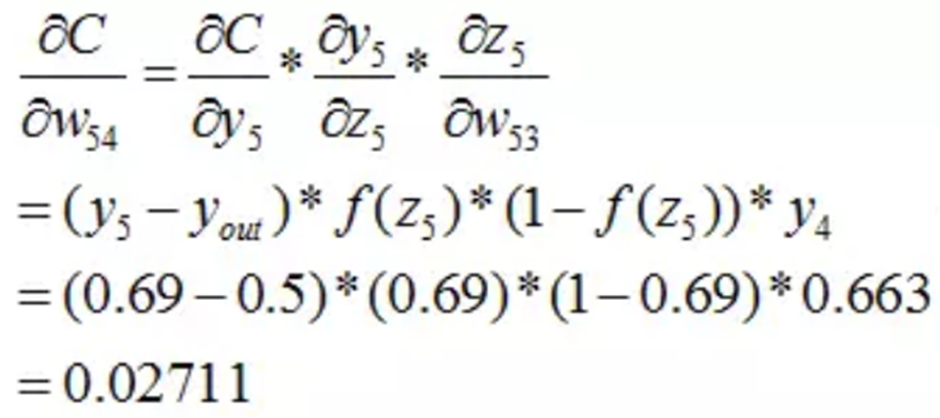
到此我們已經算出了最後一層的引數偏導了.我們繼續往前面鏈式推導:
我們現在還需要求W31,W32,W41,W42
下面給出其中的一個推到,其它完全類似:

同理可得到其它幾個式子:
則最終的結果為:
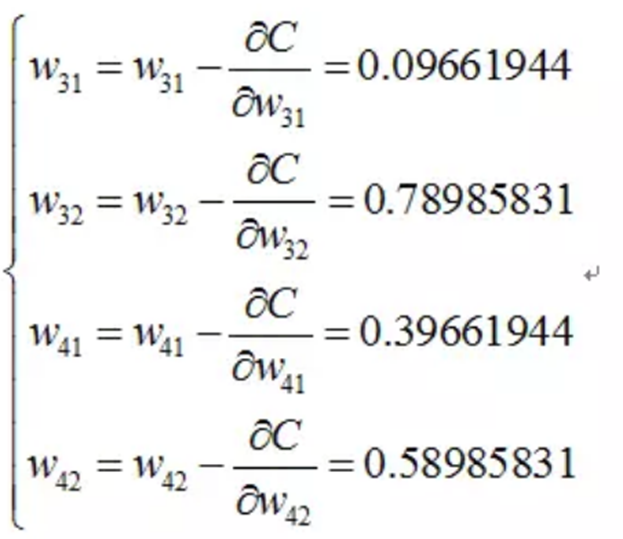
這裡,我們設定學習率=1。
再按照這個權重引數進行一遍正向傳播得出來的Error為0.165
而這個值比原來的0.19要小,則繼續迭代,不斷修正權值,使得代價函式越來越小,預測值不斷逼近0.5.我迭代了100次的結果,Error為5.92944818e-07(已經很小了,說明預測值與真實值非常接近了),最後的權值為:
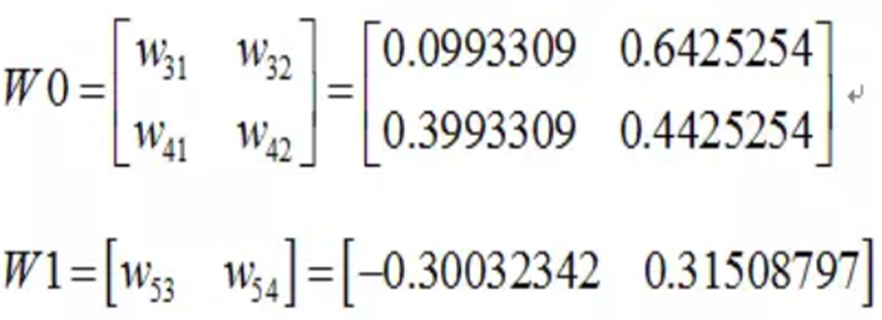
在貼出最後程式碼執行出來的結果:

(4)BP演算法的Python實現程式碼
程式碼是基於Python3.5。import numpy as np
# sigmoid function
def nonlin(x, deriv = False):
if (deriv == True):
return x * (1 - x) #如果deriv為true,求導數
return 1 / (1 + np.exp(-x)) #exp()是以e為底的指數函式
X = np.array([[0.35],[0.9]]) #輸入層
y = np.array([[0.5]]) #輸出值
np.random.seed(1)
#初始權重
W0 = np.array([[0.1,0.8],[0.4,0.6]])
W1 = np.array([[0.3,0.9]])
print("original",W0,"\n",W1)
for j in range(100):
# forward propagation
l0 = X #相當於文章中x0
l1 = nonlin(np.dot(W0,l0)) #相當於文章中y1
l2 = nonlin(np.dot(W1,l1)) #相當於文章中y2
l2_error = y - l2
Error = 1/2.0*(y - l2)**2
print("Error:",Error)
#back Propagation
l2_delta = l2_error * nonlin(l2,deriv=True) #
l1_error = l2_delta * W1 #反向傳播
l1_delta = l1_error * nonlin(l1, deriv=True)
W1 += l2_delta*l1.T; #修改權值
W0 += l0.T.dot(l1_delta)
print(W0, "\n", W1)
(5)BP神經網路的優缺點
1.BP網路優點: 1) 非線性對映能力:BP神經網路實質上實現了一個從輸入到輸出的對映功能,數學理論證明三層的神經網路就能夠以任意精度逼近任何非線性連續函式。這使得其特別適合於求解內部機制複雜的問題,即BP神經網路具有較強的非線性對映能力。2) 自學習和自適應能力:BP神經網路在訓練時,能夠通過學習自動提取輸出、輸出資料間的“合理規則”,並自適應的將學習內容記憶於網路的權值中。即BP神經網路具有高度自學習和自適應的能力。
3) 泛化能力:所謂泛化能力是指在設計模式分類器時,即要考慮網路在保證對所需分類物件進行正確分類,還要關心網路在經過訓練後,能否對未見過的模式或有噪聲汙染的模式,進行正確的分類。也即BP神經網路具有將學習成果應用於新知識的能力。
4) 容錯能力:BP神經網路在其區域性的或者部分的神經元受到破壞後對全域性的訓練結果不會造成很大的影響,也就是說即使系統在受到區域性損傷時還是可以正常工作的。即BP神經網路具有一定的容錯能力。
2.BP網路缺點: 1) 區域性極小化問題:從數學角度看,傳統的 BP神經網路為一種區域性搜尋的優化方法,它要解決的是一個複雜非線性化問題,網路的權值是通過沿區域性改善的方向逐漸進行調整的,這樣會使演算法陷入區域性極值,權值收斂到區域性極小點,從而導致網路訓練失敗。加上BP神經網路對初始網路權重非常敏感,以不同的權重初始化網路,其往往會收斂於不同的區域性極小,這也是很多學者每次訓練得到不同結果的根本原因。
2) BP 神經網路演算法的收斂速度慢:由於BP神經網路演算法本質上為梯度下降法,它所要優化的目標函式是非常複雜的,因此,必然會出現“鋸齒形現象”,這使得BP演算法低效;又由於優化的目標函式很複雜,它必然會在神經元輸出接近0或1的情況下,出現一些平坦區,在這些區域內,權值誤差改變很小,使訓練過程幾乎停頓;BP神經網路模型中,為了使網路執行BP演算法,不能使用傳統的一維搜尋法求每次迭代的步長,而必須把步長的更新規則預先賦予網路,這種方法也會引起演算法低效。以上種種,導致了BP神經網路演算法收斂速度慢的現象。
3) BP 神經網路結構選擇不一:BP神經網路結構的選擇至今尚無一種統一而完整的理論指導,一般只能由經驗選定。網路結構選擇過大,訓練中效率不高,可能出現過擬合現象,造成網路效能低,容錯性下降,若選擇過小,則又會造成網路可能不收斂。而網路的結構直接影響網路的逼近能力及推廣性質。因此,應用中如何選擇合適的網路結構是一個重要的問題。
4) 應用例項與網路規模的矛盾問題:BP神經網路難以解決應用問題的例項規模和網路規模間的矛盾問題,其涉及到網路容量的可能性與可行性的關係問題,即學習複雜性問題。
5) BP神經網路預測能力和訓練能力的矛盾問題:預測能力也稱泛化能力或者推廣能力,而訓練能力也稱逼近能力或者學習能力。一般情況下,訓練能力差時,預測能力也差,並且一定程度上,隨著訓練能力地提高,預測能力會得到提高。但這種趨勢不是固定的,其有一個極限,當達到此極限時,隨著訓練能力的提高,預測能力反而會下降,也即出現所謂“過擬合”現象。出現該現象的原因是網路學習了過多的樣本細節導致,學習出的模型已不能反映樣本內含的規律,所以如何把握好學習的度,解決網路預測能力和訓練能力間矛盾問題也是BP神經網路的重要研究內容。
6) BP神經網路樣本依賴性問題:網路模型的逼近和推廣能力與學習樣本的典型性密切相關,而從問題中選取典型樣本例項組成訓練集是一個很困難的問題。
Reference:
(1)https://www.jianshu.com/p/679e390f24bb#
(2)https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247483676&idx=1&sn=3f6a0c53b0cd9ff017f92cf55220e8fe&chksm=ebb439c8dcc3b0deb49b1ba0c8c66d0af64848bb49238135786454852ed056ca2dc7f5bbf33a&mpshare=1&scene=1&srcid=0103I306pXihp9SgKJjfbNhh#rd (文章第三四節引用了,例子寫的很好,簡單易懂)
(3)http://blog.csdn.net/jiajunlee/article/details/50456921
(4)http://blog.csdn.net/chengl920828/article/details/69946881