維納過程切片
iener[x_, y_, z_] :=
Module[{o},
o = Flatten[
RandomFunction[WienerProcess[x, y], {1, z, 1}]["SliceData",
Table[i, {i, z}]]]; o = 1 + o + Abs[Min[o]]]
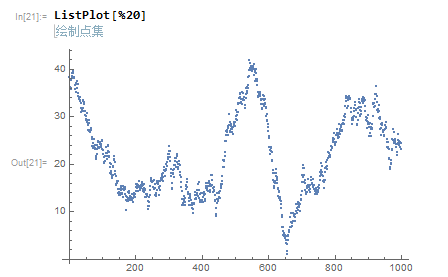
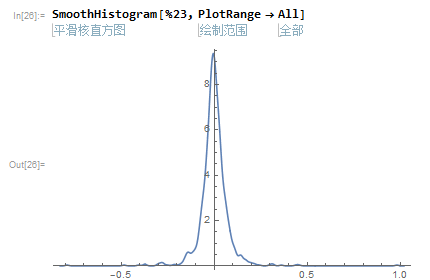
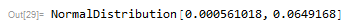
維納過程切片
相關推薦
維納過程切片
切片 ces logs -1 flat min pro matlab rand iener[x_, y_, z_] := Module[{o}, o = Flatten[ RandomFunction[WienerProcess[x, y], {1, z
維納濾波實現
wid proc 灰度 auto sig play png size and 參考鏈接:Matlab Wiener2函數 一、算法原理及公式: 二、算法實現: 步驟一:計算局部均值圖localMean與局部方差圖localVar,可采用積分圖加速;
真實美國維納斯大學畢業證書樣本原版
遞增 美國大學 解決辦法 快捷 必須 國家 QQ 親戚 事業單位 維納斯大學畢業證樣本聯系【微/Q:767161412 —— WeChat:rbdx767161412】畢業證、成績單、學歷認證、回國證明、留信網認證、留服網認證、學位證、學士證、碩士證、辦理聯系【V信:rbd
維納濾波LMS matlab
LMS演算法的前提是:參考輸入端進入的訊號與需要的訊號具有相關關係;同時與純淨的有用訊號相互獨立。 常用在干擾相消的情況下,比如心電圖訊號常常會混有50Hz的噪聲,需要慮除這個噪聲,我就可以在參考輸入的輸入一個50hz的訊號。即這個訊號與噪聲是相關的(頻率一致),故可以消除噪聲。而心電圖訊號是個
Numpy 筆記: 多維陣列的切片(slicing)和索引(indexing)【轉】
目錄 切片(slicing)操作 索引(indexing) 操作 最簡單的情況 獲取多個元素 切片和索引的同異 切片(slicing)操作 Numpy 中多維陣列的切片操作與 Py
數字影象處理 維納濾波
function [f,noise] = mywiener2(g, nhood, noise) if (nargin<3) noise = []; end % Estimate the local mean of f. localMean = fil
Wiener維納濾波基本原理及其演算法實現
文章轉載自:http://blog.sina.com.cn/s/blog_bb81c2230102xdbl.html 如果有侵權,請聯絡博主刪除 To learn, to share, to debate, then comes progress. 1.演算法背景: 訊號濾波
三維地圖新增切片“lods of null”報錯
問題描述: 將圖層的投影轉換後釋出服務,然後載入到底圖上時,關於座標系的報錯已經消失,但又出現了一個新的錯誤資訊“Cannot read property 'lods' of null at Object.g.checkIfTileIn
三維地圖新增切片圖層座標系報錯
問題描述: 在學習4.X版本的API開發時,想建立一個切片圖層並將它新增至底圖上,按照官網教程進行編寫程式碼之後執行,出現如下圖所示的錯誤: 解決方法: &nbs
03 三維地圖新增切片圖層
在介紹了建立二維、三維地圖之後,我們接下來介紹三維地圖如何新增切片圖層。地圖新增切片圖層的最終結果如下圖所示,在此過程中預設實現了將業務圖層居中顯示的效果: 具體操作如下所示: 1 建立HTML基本架構,建立
維納濾波器---看完必懂(不懂再看一遍就懂)
首先我們討論一下什麼叫濾波器,一個濾波器就是一段含有噪聲的訊號,經過這個濾波器之後,變成了另一個訊號,只不過,這個訊號比較特殊,它和原來的訊號有聯絡,這個聯絡就是現在的訊號是原來訊號的+噪聲訊號。這就是輸出訊號,和輸入訊號的相關性。 既然濾波器就是這麼一個東西h(n),我們
list迴圈、多維陣列、切片、字典基本操作
1、list迴圈 1)for迴圈 stus = ['域內','ysng','xln','yg','gx','jy'] for i in range(len(stus)): print(i) 2)while迴圈 stus = ['域內','
Python建立二維陣列和切片操作
在推薦系統的資料構造時,經常要使用二維陣列,通常先建立元素均為0的陣列,這要使用Numpy模組中的zeros()函式 1.建立一個元素為0的二維陣列: from numpy import * b=zeros((2,3))>> array([[ 0., 0.
三維重建過程與演算法介紹
一、影象預處理 影象預處理的目的在於改善影象的視覺效果,提高影象的清晰度,有選擇的突出某些感興趣的資訊,抑制 無用的資訊,以提高影象的使用價值。 影象平滑處理:中值濾波、形態學濾波、雙邊濾
自適應濾波:維納濾波器——FIR及IIR設計
作者:桂。 時間:2017-03-23 06:28:45 【讀書筆記02】 前言 仍然是西蒙.赫金的《自適應濾波器原理》第四版,距離上次看這本書已經過去半個月,要抓點緊了。本文主要包括: 1)何為維納濾波器(Wiener Filter); 2)Wiener濾波器的推導;
濾波器設計(3):維納(Wiener)濾波器的設計
引言通訊領域中,當然完全不止通訊領域,一個很常見的需求就是,從含有噪聲,或是已經畸變的訊號中,提取出或恢復出原始的、有用的訊號。怎麼做?可以用濾波器(Filter)。濾波器的變數(輸入)是訊號,訊號又是時間or空間or時間空間or…的函式。於是,函式的函式——泛函。至今,我沒
影象去模糊(維納濾波)
在數學應用上,對於運動引起的影象模糊,最簡單的方法是直接做逆濾波,但是逆濾波對加性噪聲特別敏感,使得恢復的影象幾乎不可用。最小均方差(維納)濾波用來去除含有噪聲的模糊影象,其目標是找到未汙染影象的一個估計,使它們之間的均方差最小,可以去除噪聲,同時清晰化模糊影象
維納濾波器(一)
很久沒有靜下心來整理一下了,我很早之前就想做一個從Wiener 濾波器了開始講的部落格了,現在終於有了安靜坐下來總結一下的理由。從這裡開始入手我感覺是對這一年多時間的尊敬,我會從模型開始講起,會把我從論文和書中的理解呈現出來,如果有時間,我會把我的程式碼放到我的git上,有興
卡爾曼濾波和維納濾波
--總覺得網上其他部落格上寫的都不太適合自己理解,百般翻閱書籍理解了一下,供自己日後複習之用。 本文的程式整理可到此處下載:http://download.csdn.net/download/sillykog/10123483 用過去的觀測值來估計當前或者
使用 matlab 數字影象處理(十)—— 維納濾波復原
逆濾波只能解決只有退化函式,沒有加性噪聲的問題。維納濾波又稱最小均方誤差濾波,綜合考慮了退化函式和噪聲。均方誤差由下式給出: e2=|f(x)−f^(x)|2 假定噪聲與影象是不相關的,復原影象的最佳估計可用下式表示: F^(u,v)=[HH(u,v)|H
