合並石子大總結
合並石子大總結
石子合並問題是最經典的DP問題。首先它有如下3種題型:
一、非相鄰兩堆石子合並
有N堆石子,現要將石子有序的合並成一堆,規定如下:每次只能移動任意的2堆石子合並,合並花費為新合成的一堆石子的數量。求將這N堆石子合並成一堆的總花費最小(或最大)。
分析:當然這種情況是最簡單的情況,合並的是任意兩堆,直接貪心即可,每次選擇最小的兩堆合並。本問題實際上就是哈夫曼的變形。
二、直線型相鄰兩堆石子合並
有N堆石子,現要將石子有序的合並成一堆,規定如下:每次只能移動相鄰的2堆石子合並,合並花費為新合成的一堆石子的數量。求將這N堆石子合並成一堆的總花費最小(或最大)。
有四種方法可以做這個:
(1)、
1、狀態:
f[i][j]表示從第i堆合並到第j堆的最小代價
sum[i][j]表示第i堆石子到第j堆石子的總和
最終狀態:
f[1][n]
初始狀態:
f[i][i]=0
狀態轉移方程:
f[i][j] = min(f[i][k]+f[k+1][j]+sum[i][j])(i<=k<j)
f[i][j]初始設置為INT_MAX.
2、dp過程:
三層循環,最外層枚舉一串合並的長度len,最小是2堆石子合並,最大是n堆.
然後枚舉i,那麽j就是i+len-1,在i和j之間枚舉破點k,比較.
len…2->n
i…1->n-len+1 起點
k…i->j-1

3、其它
矩陣連乘與這類問題非常相似。矩陣連乘每次也是合並相鄰兩個矩陣(只是計算方式不同)。那麽石子合並問題可用矩陣連乘的方法來解決。
那麽最優子結構是什麽呢?如果有N堆,第一次操作肯定是從n-1個對中選取一對進行合並,第二次從n-2對中選取一對進行合並,以此類推……
求出w的前綴和s,s[0]設為0,s[i]表示w[1]+w[2]+...+w[i],這樣的話w[i]+w[i+1]+...+w[j]就是s[j]-s[i-1].
f[i][j]表示從第i堆合並到第j堆的最小代價,則f[i][j] = min(f[i][k]+f[k+1][j]+s[j]-s[i-1])(i<=k<j),f[i][j]初始設置為
INT_MAX.
以長度為5的石子堆12345為例
|
下標 |
1 |
2 |
3 |
4 |
5 |
|
值 |
1 |
2 |
3 |
4 |
5 |
len為2 那麽起點的最大值就是n-len+1=4
- for(int len=2;len<=n;len++)//歸並的石子長度
- {
- for(i=1;i<=n-len+1;i++)//i為起點,j為終點
- {
- j=i+len-1; //由於len,表示有len個石子進行歸並,從i開始,由於只有相鄰的石子才能合並,所以結束位置j=i+len-1
- f[i][j]=INF; //初始值都置為無窮大
- for(k=i;k<=j-1;k++) //中間斷開位置,查找在[i,j]什麽位置設置斷點k,f[i][j]取最優值
- {
- if(f[i][j]>f[i][k]+f[k+1][j]+sum[i][j])
- 10. f[i][j]=f[i][k]+f[k+1][j]+sum[i][j];
- 11. }
- 12. }
- 13. }
DP 過程:
階段:以歸並石子的長度為階段,一共有n-1個階段。
狀態:每個階段有多少堆石子要歸並,當歸並長度為2時,有n-1個狀態;
當歸並長度為3時,有n-2個狀態;
當歸並長度為n時,有1個狀態。
決策:當歸並長度為2時,有1個決策;當歸並長度為3時,有2個決策;
當歸並長度為n時,有n-1個決策。
(2)、
狀態:
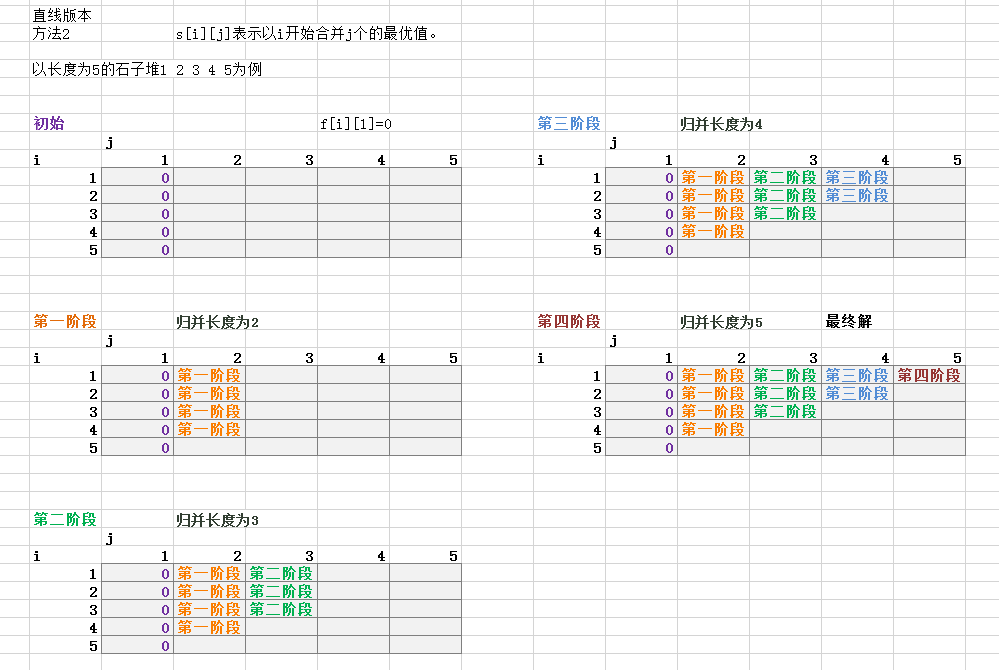
s[i][j]表示以i開始合並j個的最優值。
sum[i][j]表示第i堆石子到第j堆石子的總和
最終狀態:
s[1][n]
初始狀態
s[i][1]=0
狀態轉移方程:
以i開始的k個,結束下標為i+k-1
k表示從i開始合並的個數
f[i][j] = min(f[i][k]+f[i+k][j-k]+sum[i][i+j-1])(0<=k<j)
f[i][j]初始設置為INT_MAX.
以長度為5的石子堆12345為例
|
下標 |
1 |
2 |
3 |
4 |
5 |
|
值 |
1 |
2 |
3 |
4 |
5 |
例如i=1 j=5 k=2
f[1][5]= f[1][2]+ f[3][3]+ sum[1][5]
dp過程:
j…1->n
i…1->n-j+1
k…1->j
那麽下面就是每一個階段的具體合並
初始階段就是s[1,1],s[2,1],s[3,1],s[4,1],s[5,1],因為一開始還沒有合並,所以這些值應該全部為0。
第二階段:兩兩合並過程如下,其中sum(i,j)表示從i開始數j個數的和
s[1,2]=s[1,1]+s[2,1]+sum(1,2)
s[2,2]=s[2,1]+s[3,1]+sum(2,2)
s[3,2]=s[3,1]+s[4,1]+sum(3,2)
s[4,2]=s[4,1]+s[5,1]+sum(4,2)
第三階段:三三合並可以拆成兩兩合並,拆分方法有兩種,前兩個為一組或後兩個為一組
s[1,3]=s[1,2]+s[3,1]+sum(1,3)或s[1,3]=s[1,1]+s[2,2]+sum(1,3),取其最優
s[2,3]=s[2,2]+s[4,1]+sum(2,3)或s[1,3]=s[2,1]+s[3,2]+sum(2,3),取其最優
.
.
.
第四階段:四四合並的拆分方法用三種,同理求出三種分法的得分,取其最優即可。
以此類推
(3)、
狀態:
dp[i][j]表示以i開始合並j次的最優值。
sum[i][j]表示第i堆石子到第j堆石子的總和
最終狀態:
dp[1][n-1]
初始狀態:
dp[i][0]
狀態轉移方程:
dp[i][j]=min(dp[i][k]+dp[i+k+1][j-k-1]+sum[i][j])(0<k<=j-1)
dp過程:
j…1->n-1
i…1->n-j
k…1->j-1

(4)、
狀態:
f[i][j]表示從第i堆合並到第j堆的最小代價
s[i]表示前i堆石子的和
最終狀態:
f[1][n]
初始狀態:
f[i][i]=0
狀態轉移方程:
f[i][j] = min(f[i][k]+f[k+1][j]+s[j]-s[i-1])(i<=k<j)
f[i][j]初始設置為INT_MAX.
dp過程:
i…n->1
j…i+1->n
k…i->j-1

參考代碼:
1 #include <iostream> 2 #include <string.h> 3 #include <stdio.h> 4 5 using namespace std; 6 const int INF = 1 << 30; 7 const int N = 205; 8 9 int dp[N][N]; 10 int sum[N]; 11 int a[N]; 12 13 int getMinval(int a[],int n) 14 { 15 for(int i=0;i<n;i++) 16 dp[i][i] = 0; 17 for(int v=1;v<n;v++) 18 { 19 for(int i=0;i<n-v;i++) 20 { 21 int j = i + v; 22 dp[i][j] = INF; 23 int tmp = sum[j] - (i > 0 ? sum[i-1]:0); 24 for(int k=i;k<j;k++) 25 dp[i][j] = min(dp[i][j],dp[i][k]+dp[k+1][j] + tmp); 26 } 27 } 28 return dp[0][n-1]; 29 } 30 31 int main() 32 { 33 freopen("mergerStone2.txt","r",stdin); 34 int n; 35 while(scanf("%d",&n)!=EOF) 36 { 37 for(int i=0;i<n;i++) 38 scanf("%d",&a[i]); 39 sum[0] = a[0]; 40 for(int i=1;i<n;i++) 41 sum[i] = sum[i-1] + a[i]; 42 printf("%d\n",getMinval(a,n)); 43 } 44 return 0; 45 }
三、環型相鄰兩堆石子合並

上面的四種直線型相鄰兩堆石子合並都可以修改少量代碼後變成環型相鄰兩堆石子合並的解。
方法一:環化成兩倍線長
方法二:%n
(1)、
因為圓形是首尾相接的,初一想,似乎與直線排列完全成了兩個不同的問題。因為每次合並後我們都要考慮最後一個與第一個的合並關系。直線版的最優子結構不見了。f(i, j)表示i—>j合並的最優值似乎並不可行,因為我們可以得到的最優值第一步就是第一個與最後一個合並,那麽f(i, j)並不能表示這種關系。
但是可以用兩倍線性長的方法。
去看4吧。
(2)、
狀態:
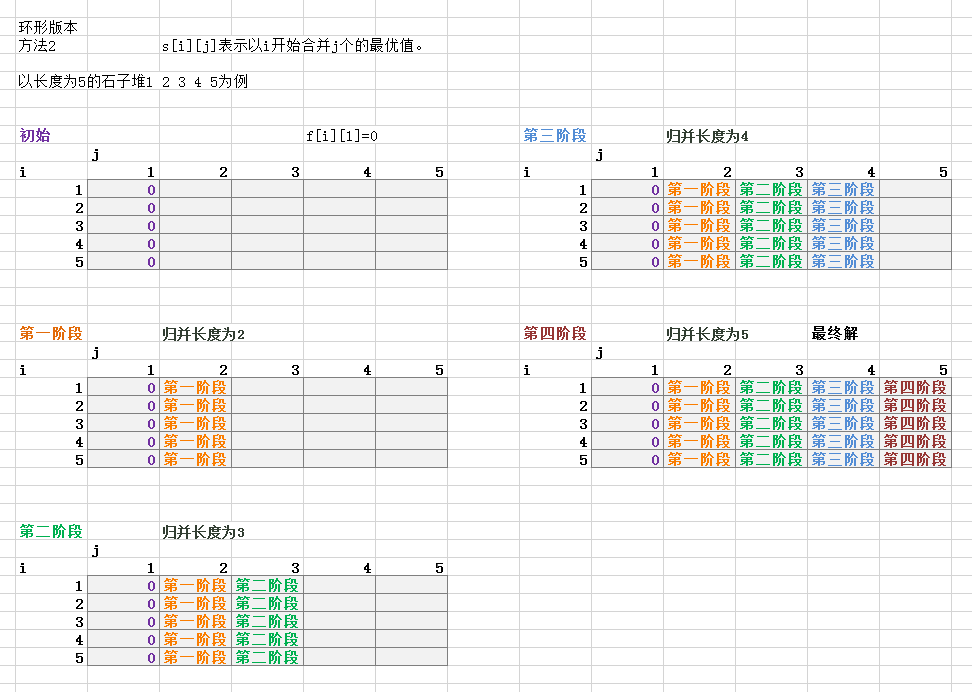
s[i][j]表示以i開始合並j個的最優值。
sum[i][j]表示第i堆石子到第j堆石子的總和
最終狀態:
max(s[1][n])
初始狀態
s[i][1]=0
狀態轉移方程:
以i開始的k個,結束下標為i+k-1
k表示從i開始合並的個數
f[i][j] = min(f[i][k]+f[(i+k)%n][j-k]+sum[i][i+j-1])(0<=k<j)
f[i][j]初始設置為INT_MAX.
以長度為5的石子堆12345為例
|
下標 |
1 |
2 |
3 |
4 |
5 |
|
值 |
1 |
2 |
3 |
4 |
5 |
例如i=1 j=5 k=2
f[1][5]= f[1][2]+ f[3][3]+ sum[1][5]
dp過程:
j…1->n
i…1->n
k…1->j
(3)、
狀態:
dp[i][j]表示以i開始合並j次的最優值。
sum[i][j]表示第i堆石子到第j堆石子的總和
最終狀態:
max(dp[i][n-1])
初始狀態:
dp[i][0]=0
狀態轉移方程:
dp[i][j]=min(dp[i][k]+dp[(i+k+1)%n][j-k-1]+sum[i][j])(0<k<=j-1)

dp過程:
j…1->n-1
i…1->n
k…1->j-1
以長度為5的石子堆12345為例
|
下標 |
1 |
2 |
3 |
4 |
5 |
|
值 |
1 |
2 |
3 |
4 |
5 |
例如當j等於1(也就是合並一次,兩個數),那麽i的取值範圍是(1,n-j+1)=(1,5)
就是保證有5 1這次合並
所以j為1時候的合並為(1,2),(2,3),(3,4),(4,5),(5,1)

註意和直線的時候的運行過程做對比。
(4)、
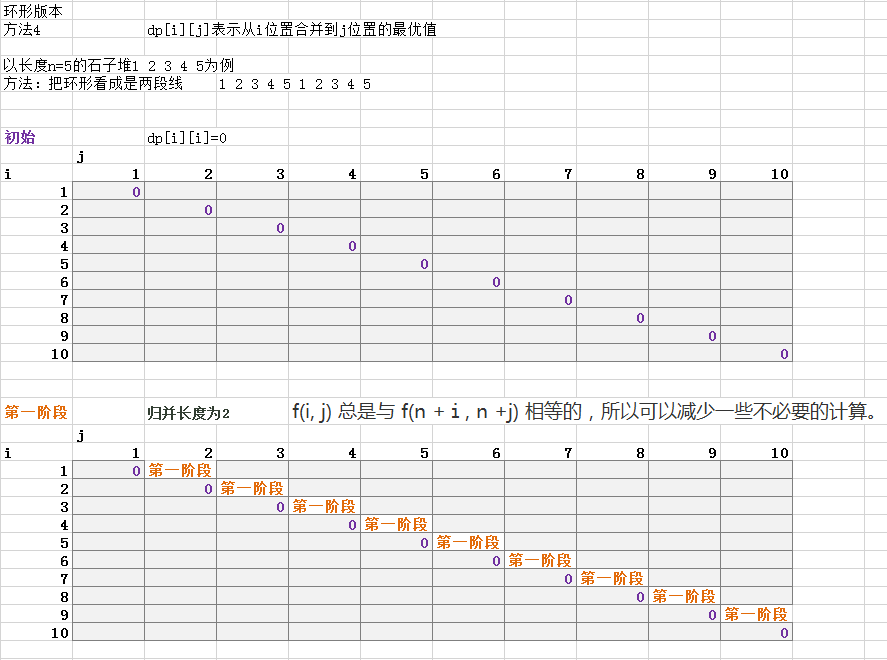
環形結構,經常采用雙倍長度線性化手段,也就是說,把環形結構看成是長度為環的兩倍的線性結構來處理。
環的長度是N,所以題目相當於有一排石子1....N+1....N,然後就可以用線性的石子合並問題的方法做了。
有個要註意的地方,f(i, j) 總是與 f(N +i, N +j) 相等的,所以可以減少一些不必要的計算。
此題的關鍵在於化環為線性結構,與N個數圍成一圈,連續多少個數的最大和,異曲同工。
將N結構的線性表,轉換為雙倍長度的2N結構的線性表,然後在2N長度的表中,截取我們需要的長度為N的部分就可以了。
狀態:
f[i][j]表示從第i堆合並到第j堆(合並成一堆的)的最小代價
s[i]表示前i堆石子的和
最終狀態:
初始狀態:
f[i][i]=0
狀態轉移方程:
f[i][j] = min(f[i][k]+f[k+1][j]+s[j]-s[i-1])(i<=k<j)
f[i][j]初始設置為INT_MAX.
dp過程:
len…1->n len表示歸並的長度
i…1->2n i表示起點
那麽j=i+len-1
k…i->j-1

參考代碼:
1 #include <iostream> 2 #include <string.h> 3 #include <stdio.h> 4 5 using namespace std; 6 const int INF = 1 << 30; 7 const int N = 205; 8 9 int mins[N][N]; 10 int maxs[N][N]; 11 int sum[N],a[N]; 12 int minval,maxval; 13 int n; 14 15 int getsum(int i,int j) 16 { 17 if(i+j >= n) return getsum(i,n-i-1) + getsum(0,(i+j)%n); 18 else return sum[i+j] - (i>0 ? sum[i-1]:0); 19 } 20 21 void Work(int a[],int n) 22 { 23 for(int i=0;i<n;i++) 24 mins[i][0] = maxs[i][0] = 0; 25 for(int j=1;j<n;j++) 26 { 27 for(int i=0;i<n;i++) 28 { 29 mins[i][j] = INF; 30 maxs[i][j] = 0; 31 for(int k=0;k<j;k++) 32 { 33 mins[i][j] = min(mins[i][j],mins[i][k] + mins[(i+k+1)%n][j-k-1] + getsum(i,j)); 34 maxs[i][j] = max(maxs[i][j],maxs[i][k] + maxs[(i+k+1)%n][j-k-1] + getsum(i,j)); 35 } 36 } 37 } 38 minval = mins[0][n-1]; 39 maxval = maxs[0][n-1]; 40 for(int i=0;i<n;i++) 41 { 42 minval = min(minval,mins[i][n-1]); 43 maxval = max(maxval,maxs[i][n-1]); 44 } 45 } 46 47 int main() 48 { 49 freopen("mergerStone3.txt","r",stdin); 50 while(scanf("%d",&n)!=EOF) 51 { 52 for(int i=0;i<n;i++) 53 scanf("%d",&a[i]); 54 sum[0] = a[0]; 55 for(int i=1;i<n;i++) 56 sum[i] = sum[i-1] + a[i]; 57 Work(a,n); 58 //printf("%d %d\n",minval,maxval); 59 printf("%d\n",minval); 60 } 61 return 0; 62 }
合並石子大總結
