[數學建模]蒙特卡羅方法
1.概念
蒙特卡羅方法(隨機取樣法)是一種計算方法。原理是通過大量隨機樣本,去了解一個系統,進而得到所要計算的值。
2.兩個應用例子
例子1:求π的值。
正方形內部有一個相切的圓,它們的面積之比是π/4。現在,在這個正方形內部,隨機產生1000000個點(即1000000個坐標對 (x, y)),計算它們與中心點的距離,從而判斷是否落在圓的內部。如果這些點均勻分布,那麽圓內的點應該占到所有點的 π/4,因此將這個比值乘以4,就是π的值。

MATLAB實現:
N=1000000; %隨機點的數目
x=rand(N,1); %rand 生成均勻分布的偽隨機數。分布在(0~1)之間
y=rand(N,1); %矩陣的維數為N×1
count=0;
for i=1:N
if (x(i)^2+y(i)^2<=1)
count=count+1;
end
end
PI=4*count/N
例子2:計算積分
計算函數 y = x^2 在 [0, 1] 區間的積分,就是求出紅色曲線下面的面積。這個函數在 (1,1) 點的取值為1,所以整個紅色區域在一個面積為1的正方形裏面。在該正方形內部,產生大量隨機點,可以計算出有多少點落在紅色區域(判斷條件 y < x^2)。這個比重就是所要求的積分值。
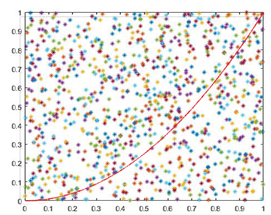
MATLAB實現:
clear
clc
N=10000;
x=rand(N,1);
y=rand(N,1);
count=0;
for i=1:N
if (y(i)<=x(i)^2)
count=count+1;
end
end
result=count/N
3. 與拉斯維加斯方法的比較
(1)蒙特卡羅算法:假如筐裏有100個蘋果,讓我每次閉眼拿1個,挑出最大的。於是我隨機拿1個,再隨機拿1個跟它比,留下大的,再隨機拿1個……我每拿一次,留下的蘋果都至少不比上次的小。拿的次數越多,挑出的蘋果就越大,但我除非拿100次,否則無法肯定挑出了最大的。——盡量找好的,但不保證是最好的。
特點:采樣越多,越近似最優解;
(2)拉斯維加斯方法:假如有一把鎖,給我100把鑰匙,只有1把是對的。於是我每次隨機拿1把鑰匙去試,打不開就再換1把。我試的次數越多,打開(最優解)的機會就越大,但在打開之前,那些錯的鑰匙都是沒有用的。——盡量找最好的,但不保證能找到。
特點:采樣越多,越有機會找到最優解。
4.更深度的應用
蒙特卡洛樹搜索---深度學習,強化學習
[數學建模]蒙特卡羅方法
