在深度網路中，不同層的學習速度差異很大。尤其是在網路後面層學習的情況很好的時候，先前的層常常會在訓練時停止不變，基本上學不到東西，這些原因是與基於梯度的學習方法有關。
我們用MNIST數字分類問題作為研究和實驗的物件：
這個網路有784個輸入神經元，對應於圖片28*28=784個畫素點，我們設定隱藏神經元為30個，輸出層為10個神經元，對應於MNIST的10個數字（0~9），我們訓練30epochs，使用minibatch大小為10，學習率為0.01，正則化引數為5.0。在訓練時我們也會在驗證集上監控分類的準確度。最總我們得到分類準確率為96.48%。
現在另外增加一個隱藏層，同樣地是 30 個神經元，試著使用相同的超引數進行訓練：

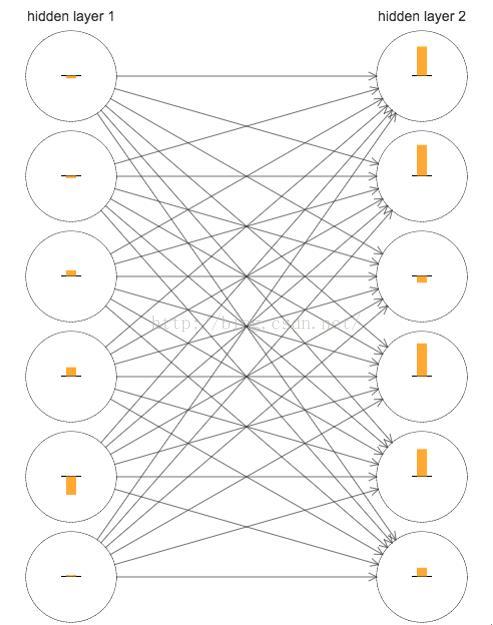
下面，畫出了一部分[784, 30, 30, 10] 的網路，也就是包含兩層各有30 個隱藏神經元的隱藏層。圖中的每個神經元有一個條形統計圖，表示這個神經元在網路進行學習時改變的速度。更大的條意味著更快的速度，而小的條則表示變化緩慢。更加準確地說，這些條表示了每個神經元上的cost function關於偏置項b的偏導數，也就是代價函式關於神經元的偏差更變的速率delta。因為我們知道delta的數值不僅僅是在學習過程中偏差改變的速度，而且也控制了輸入到神經元權重的變數速度。

從上圖中我們可以明顯的發現這樣一個規律，第二個隱藏層上的數值基本上都要比第一個隱藏層上的要大。所以，在第二個隱藏層的神經元將學習得更加快速。為了進一步解釋上一結論，使用一種全域性的方式來比較學習的速度。我們使用向量delta1和delta2分別表示第一個和第二個隱藏層的學習速率，向量中的每個元素表示該層上每個神經元的小學習速率：

所以，我們可以使用這些向量的長度作為全域性衡量這些隱藏層的學習速度的度量。||delta1|| 就代表第一層隱藏層學習速度，而||delta2|| 就代表第二層隱藏層學習速度。

藉助這些定義，在和上圖同樣的配置下，發現||delta1|| = 0.07而||delta2|| =0.31，所以通過數量上的計算也說明了在第二層隱藏層的神經元學習速度確實比第一層要快。

對於三個隱藏層的情況，比如在[784, 30, 30, 30, 10] 的網路中，那麼對應的學習速度就是 0.012, 0.060, 0.283。也證明了我們上面的結論。假設我們增加另一個包含30 個隱藏神經元的隱藏層[784, 30, 30, 30, 30, 10] 對應的學習速度是：0.003,0.017, 0.070, 0.285。還是同樣說明了前面的層學習速度低於後面的層。

上述的全域性速度的計算是剛剛初始化之後的情況。隨著訓練的推移學習速度變化如下：

對於只有兩個隱藏層時net([784, 30, 30, 10])，為了防止使用minibatch隨機梯度下降對結果帶來更多的噪聲，我在 1000 個訓練影象上進行了 500 輪 batch 梯度下降，而沒有使用minibatch方法。
如圖所示，兩層在開始時就有著不同的速度。然後兩層的學習速度在觸底前迅速下落。在最後，我們發現第一層的學習速度變得比第二層更慢了。

對於有四個隱藏層時net([784, 30, 30, 30, 30, 10])，也可以得到與前兩種情況相同的結論：前面的隱藏層要比後面的隱藏層學習的更慢。這裡，第一層的學習速度和最後一層要差了兩個數量級，也就是比第四層慢了100倍，這就比較容易解釋為什麼在MNIST手寫數字識別時，4個隱藏層的網路的效果並沒有比2個隱藏層的要好，因為這種速度的下降從另一個角度看實際上是梯度的消失，即使隱藏層多了，但是卻並沒有學到知識。上述的現象就是我們在深度學習中經常會遇到的梯度彌散問題（vanishing gradient problem）或梯度消失問題

相似的，對於在前面的層中的梯度會變得非常的情況稱為爆炸的梯度問題（exploding gradient problem）或梯度膨脹問題。更加一般地說，在深度神經網路中的梯度是不穩定的，在前面的層中或會消失，或會爆炸。這種不穩定性才是深度神經網路中基於梯度學習的根本問題。這就是我們需要理解的東西，如果可能的話，採取合理的步驟措施解決問題。

為了進一步弄清楚為何會出現消失的梯度，來看看一個極簡單的深度神經網路：每一層都只有一個單一的神經元。下圖就是有三層隱藏層的神經網路：

下面求目標函式C關於第一個神經元的梯度：

先看看下面的sigmoid 函式導數的影象：

也就是說sigmoid函式的導數在0出取得最大值1/4。現在，如果我們使用標準方法來初始化網路中的權重，那麼會使用一個均值為0 標準差為 1 的高斯分佈。因此所有的權重通常會滿足|wj| < 1。所以權重與sigmiod函式導數的乘積是小於1/4的。並且在我們進行了所有這些項的乘積時，最終結果肯定會指數級下降：項越多，乘積的下降的越快。這裡我們可以理解了消失的梯度問題的合理解釋。

比較目標函式關於第三個神經元和第一個神經元的梯度值，兩個表示式有很多相同的項。但是後者還多包含了兩個項。由於這些項都是小於1/4的，所以後者的梯度值是前者的 1/16 或者更小。這其實就是消失的梯度出現的本質原因了。

如果乘積項變得很大超過 1，那麼我們將不再遇到消失的梯度問題，這時候梯度會在我們 BP 的時候發生指數級地增長。也就是說，我們遇到了梯度爆炸或梯度膨脹的問題，但由於目前我們的初始化策略以及所使用的啟用函式的關係，梯度膨脹問題很少出現。

梯度彌散和梯度膨脹都屬於不穩定的梯度問題：根本的問題其實是在前面的層上的梯度是來自後面的層上項的乘積。當存在過多的層次時，就出現了內在本質上的不穩定場景。唯一讓所有層都接近相同的學習速度的方式是所有這些項的乘積都能得到一種平衡。如果沒有某種機制或者更加本質的保證來達成平衡，那網路就很容易不穩定了。簡而言之，真實的問題就是神經網路受限於不穩定梯度的問題。所以，如果我們使用標準的基於梯度的學習演算法，在網路中的不同層會出現按照不同學習速度學習的情況。