梯度下降與梯度上升的區別
我們往往能看到在對模型進行優化時,有的說用梯度下降,有的說用梯度上升,這是為什麼呢。最主要是因為目標不一樣,梯度下降是求區域性極小值,而梯度上升是求區域性最大值。
如logistic的目標函式:
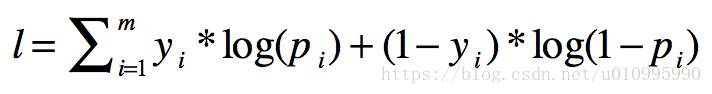
這裡的優化目標是出現的概率值,我們要求概率的最大值,也就是MLE(極大似然估計),所以用梯度上升法。
而線性迴歸的代價函式為:
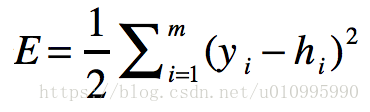
優化的目標值是誤差,我們要求誤差最小值,所以使用的是梯度下降演算法。
相關推薦
梯度下降與梯度上升的區別
我們往往能看到在對模型進行優化時,有的說用梯度下降,有的說用梯度上升,這是為什麼呢。最主要是因為目標不一樣,梯度下降是求區域性極小值,而梯度上升是求區域性最大值。 如logistic的目標函式: 這裡的優化目標是出現的概率值,我們要求概率的最大值,也
對數幾率回歸法(梯度下降法,隨機梯度下降與牛頓法)與線性判別法(LDA)
3.1 初始 屬性 author alt closed sta lose cnblogs 本文主要使用了對數幾率回歸法與線性判別法(LDA)對數據集(西瓜3.0)進行分類。其中在對數幾率回歸法中,求解最優權重W時,分別使用梯度下降法,隨機梯度下降與牛頓法。 代碼如下:
最小二乘法和梯度下降法有哪些區別?
https://www.zhihu.com/question/20822481 最小二乘法的目標:求誤差的最小平方和,對應有兩種:線性和非線性。線性最小二乘的解是closed-form即,而非線性最小二乘沒有closed-form,通常用迭代法求解。 迭代法,即在每一步update未知量逐漸
【Ian Goodfellow課件】梯度下降與神經網路代價函式的結構
本課件主要內容包括: 導數與二階導數 方向曲率 泰勒級數近似 臨界點 牛頓法 牛頓法失效的情況 為何不會收斂? 鞍點或區域性極小值更常見嗎? 為何優化過程如此之慢? 二維子空間視覺化
梯度下降與隨機梯度下降概念詳解及推導過程
同這一張的梯度下降部分加起來,才是我們要講的如何求解多元線性迴歸.如果寫在一章中,內容過長,擔心有的同學會看不完,所以拆分成兩章.[壞笑] 上一章中有提到利用解析解求解多元線性迴歸,雖然看起來很方便,但是在解析解求解的過程中會涉及到矩陣求
從最初的感動開始--數值計算【1】--梯度下降與牛頓法
直觀來說,牛頓法因為使用了二階導資訊,比單純的一階導數的梯度下降法,其發現極值點回收斂得更快。 我個人的理解,梯度下降考慮了函式值下降最快的方向(梯度方向)。而在有些情況下,按這樣的規則改變自變數取值,可能會走彎路。 其根本原因在於,梯度下降法,能夠保證函式值在改點處的變化
《白話深度學習與Tensorflow》學習筆記(2)梯度下降、梯度消失、引數、歸一化
1、CUDA(compute unified device architecture)可用於平行計算: GTX1060 CUDA核心數:1280 視訊記憶體大小:6G 2、隨機梯度下降:計算偏導數需要的計算量很大,而採用隨機梯度下降(即採用取樣的概念)從中提取一部分樣
梯度下降法(上升法)的幾何解釋
梯度下降法是機器學習和神經網路學科中我們最早接觸的演算法之一。但是對於初學者,我們對於這個演算法是如何迭代執行的從而達到目的有些迷惑。在這裡給出我對這個演算法的幾何理解,有不
機器學習案例——梯度下降與邏輯迴歸簡單例項
梯度下降例項 下圖是f(x) = x2+3x+4 的函式影象,這是初中的一元二次函式,它的導數為g(x) = f’(x) = 2x+3。我們很明確的知道,當x = -1.5時,函式取得最小值。 下面就通過梯度下降法來計算函式取最小值時x的
AdamOptimizer和隨機梯度下降法SGD的區別
Adam 這個名字來源於adaptive moment estimation,自適應矩估計,如果一個隨機變數 X 服從某個分佈,X 的一階矩是 E(X),也就是樣本平均值,X 的二階矩就是 E(X^2),也就是樣本平方的平均值。Adam 演算法根據損失函式對每個引數的梯度
感知機3 -- 梯度下降與隨機梯度下降的對比
宣告: 1,本篇為個人對《2012.李航.統計學習方法.pdf》的學習總結,不得用作商用,歡迎轉載,但請註明出處(即:本帖地址)。 2,由於本人在學習初始時有很多數學知識都已忘記,所以為了弄懂其中的內容查閱了很多資料,所以裡面應該會有引用
梯度下降與delta法則
delta法則 儘管當訓練樣例線性可分時,感知器法則可以成功地找到一個權向量,但如果樣例不是線性可分時它將不能收斂。 因此,人們設計了另一個訓練法則來克服這個不足,稱為 delta 法則(delta rule)。如果訓練樣本不是線性可分的,那麼 delta 法則會收斂到目
梯度彌散與梯度彌散
損失函數 tput ges xpl 參考文獻 聯合 其他 等等 image 問題描述 先來看看問題描述。 當我們使用sigmoid funciton 作為激活函數時,隨著神經網絡hidden layer層數的增加,訓練誤差反而加大了,如上圖所示。 下面以2層隱藏層神經網
梯度下降 隨機梯度下降 批量梯度下降
函數 算法 學習 梯度 target 最快 每次 深度學習 sun 梯度下降(GD) 梯度的本意是一個向量,表示某一函數在該點處的方向導數沿著該方向取得最大值,導數對應的是變化率 即函數在該點處沿著該方向變化最快,變化率最大(為該梯度的模) 隨機梯度下降(SGD):每次叠代
梯度下降 隨機梯度下降 演算法
一、一維梯度下降 演算法思想: 我們要找到一個函式的谷底,可以通過不斷求導,不斷逼近,找到一個函式求導後為0,我們就引入了一個概念 學習率(也可以叫作步長),因為是不斷逼近某個x,所以學習率過大會導致超過最優解,而學習率過小,會導致收斂速度過慢。 二、多維梯度下降
梯度爆炸與梯度消失
梯度消失: 這種情況往往在神經網路中選擇了不合適的啟用函式時出現。如神經網路使用sigmoid作為啟用函式,這個函式有個特點,就是能將負無窮到正無窮的數對映到0和1之間,並且對這個函式求導的結果是f′
梯度爆炸與梯度消失的原因以及解決方法,區域性極小值問題以及學習率問題(對SGD的改進)
梯度爆炸與梯度消失的原因:簡單地說,根據鏈式法則,如果每一層神經元對上一層的輸出的偏導乘上權重結果都小於1的話( ),那麼即使這個結果是0.99,在經過足夠多層傳播之後,誤差對輸入層的偏導會趨於0( )。下面是數學推導推導。假設網路輸出層中的第 個神經元輸出為,而要學習的目標
梯度消失與梯度爆炸總結
神經網路中梯度消失與梯度爆炸問題綜述前言隨著計算資源和資料量的增加,深度學習方法又再次回到公眾的視野。但是隨著深度的增加,神經網路的訓練越來越難,一個重要的原因是,深度的增加會導致梯度消失和梯度爆炸問題的出現,使網路權重難以訓練。文章分為兩部分,第一部分簡單介紹梯度消失和
[深度學習] 梯度消失與梯度爆炸的原因及解決方法
前言本文主要深入介紹深度學習中的梯度消失和梯度爆炸的問題以及解決方案。本文分為三部分,第一部分主要直觀的介紹深度學習中為什麼使用梯度更新,第二部分主要介紹深度學習中梯度消失及爆炸的原因,第三部分對提出梯度消失及爆炸的解決方案。有基礎的同鞋可以跳著閱讀。 其中,梯度消失爆炸的解
梯度消失與梯度爆炸
LSTM 與 Gradient Vanish 上面說到,LSTM 是為了解決 RNN 的 Gradient Vanish 的問題所提出的。關於 RNN 為什麼會出現 Gradient Vanish,上面已經介紹的比較清楚了,本質原因就是因為矩陣高次冪導致的。下面簡要解釋一下為什麼 LSTM 能有效避免 Gr
