P1283 平板塗色
P1283 平板塗色
題目描述
CE數碼公司開發了一種名為自動塗色機(APM)的產品。它能用預定的顏色給一塊由不同尺寸且互不覆蓋的矩形構成的平板塗色。
為了塗色,APM需要使用一組刷子。每個刷子塗一種不同的顏色C。APM拿起一把有顏色C的刷子,並給所有顏色為C且符合下面限制的矩形塗色:
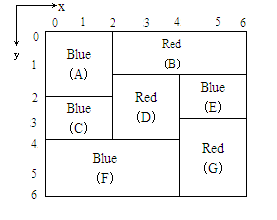
為了避免顏料滲漏使顏色混合,一個矩形只能在所有緊靠它上方的矩形塗色後,才能塗色。例如圖中矩形F必須在C和D塗色後才能塗色。註意,每一個矩形必須立刻塗滿,不能只塗一部分。
寫一個程序求一個使APM拿起刷子次數最少的塗色方案。註意,如果一把刷子被拿起超過一次,則每一次都必須記入總數中。
輸入輸出格式
輸入格式:
第一行為矩形的個數N。下面有N行描述了N個矩形。每個矩形有5個整數描述,左上角的y坐標和x坐標,右下角的y坐標和x坐標,以及預定顏色。
顏色號為1到20的整數。
平板的左上角坐標總是(0, 0)。
坐標的範圍是0..99。
N小於16。
輸出格式:
輸出至文件paint.out,文件中記錄拿起刷子的最少次數。
輸入輸出樣例
輸入樣例#1:7 0 0 2 2 1 0 2 1 6 2 2 0 4 2 1 1 2 4 4 2 1 4 3 6 1 4 0 6 4 1 3 4 6 6 2輸出樣例#1:
3
分析:
來自洛谷題解 1、一看到n<=16,顏色<=20,馬上就要想到裸的狀壓dp,
設dp[S][i]表示在集合S(已經塗的矩形的集合)中,最後塗色的顏色是i,所需的最少拿刷子的次數。至於集合,就是用二進制表示。
先預處理出每個矩形上面有哪些矩形,這個由於數據範圍比較小,都不用離散化,直接開個二維數組弄個矩形覆蓋就行了。
至於具體的Dp,應該還算是比較好寫的。
枚舉一下最後一次塗的是第j個矩形,而第j個矩形的顏色是col[j],當然,這個第j個矩形必須滿足兩個限制:
1.j屬於S
2.j上面的矩形都屬於S
那麽Dp(S,col[j])=min(Dp(S-(1<<(j-1)),k)+1){枚舉另一個顏色k,並且k!=col[j]}
Dp(S,col[j])=min(Dp(S-(1<<(j-1)),col[j]))
這個還是很好理解的。
參考代碼:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 template<class T>void ChkMin(T &a,T b){if (a>b)a=b;} 6 const int INF=0x3f3f3f3f; 7 const int N=101; 8 const int M=21; 9 int lx[M],size[M],ly[M],col[M],rx[M],ry[M]; 10 int n,a[N][N],dp[1<<16+1][M],up[M][M]; 11 inline bool in(int i,int S){ 12 return (S>>(i-1))&1; 13 } 14 inline bool ok(int i,int S){ 15 bool flag=true; 16 for (int j=1;j<=size[i] && flag;j++)flag&=in(up[i][j],S); 17 return flag; 18 } 19 int main(){ 20 scanf("%d",&n); 21 for (int i=1;i<=n;i++){ 22 scanf("%d%d%d%d%d",&lx[i],&ly[i],&rx[i],&ry[i],&col[i]); 23 for (int x=lx[i];x<rx[i];x++) 24 for (int y=ly[i];y<ry[i];y++) 25 a[x][y]=i; 26 } 27 for (int i=1;i<=n;i++){ 28 if (!lx[i])continue; 29 lx[i]--; 30 for (int j=ly[i]+1;j<=ry[i];j++) 31 if (a[lx[i]][j]!=a[lx[i]][j-1])up[i][++size[i]]=a[lx[i]][j-1]; 32 if (a[lx[i]][ry[i]]==a[lx[i]][ry[i]-1])up[i][++size[i]]=a[lx[i]][ry[i]-1]; 33 } 34 memset(dp,0x3f,sizeof(dp)); 35 for (int i=1;i<=20;i++) 36 dp[0][i]=1; 37 for (int i=1;i<(1<<n);i++){ 38 for (int j=1;j<=n;j++) 39 if (in(j,i) && ok(j,i)){ 40 for (int k=1;k<=20;k++) 41 if (k!=col[j])ChkMin(dp[i][col[j]],dp[i-(1<<(j-1))][k]+1); 42 ChkMin(dp[i][col[j]],dp[i-(1<<(j-1))][col[j]]); 43 } 44 } 45 int ans=INF; 46 for (int i=1;i<=20;i++) 47 ChkMin(ans,dp[(1<<n)-1][i]); 48 printf("%d",ans); 49 return 0; 50 }
2、
看到數據範圍: n < 16 ?直接搜索,但是應該要剪枝
搜索思路
讀入數據,統計顏色,然後每個顏色都試一遍,即把該顏色的且能塗的磚塗上。
下一次塗色不能塗上次塗過的色。塗完了記錄結果
為了不超時,加了兩個剪枝
-
最優化剪枝:當前塗色次數大於等於當前答案,直接退出(這個好理解吧)
- 可行性剪枝:如果當前沒有塗到一個磚,直接退出(如果接著搜,會多一個次數,可能還會死循環,,,)
至於判斷該磚是否能塗,先預處理,把緊鄰該磚上方的磚用數組記錄下來,再判斷那些磚是否被塗
代碼如下(格式醜勿噴)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<cstdlib> 7 using namespace std; 8 struct lbq //結構體 a1b1 該磚左上角坐標 a2b2 右下角坐標 x 顏色 9 { 10 int a1,b1,a2,b2,x; 11 }a[20]; 12 int ccmp(lbq a,lbq b) 13 { 14 if(a.a1!=b.a1) return a.a1<b.a1; 15 return a.b1<b.b1; 16 } 17 bool d=false; 18 int de[20]={0};//de數組表示是否有該顏色 19 int n,m,ans=999,b[20],fk[20][20]; //b數組代表該磚是否被塗 fk[i][j]表示第i個磚是否緊鄰上方第j個磚 m 最大顏色編號 20 bool OK(int o) 21 { 22 for(int i=1;i<=n;i++) 23 if(fk[o][i]&&!b[i]) return false; //如果i磚下面緊鄰o,但i沒塗過,返回false 24 return true; 25 } 26 void dfs(int o,int pq,int xx) //o 塗色次數 pq 塗過顏色的磚 xx 上次塗的顏色 27 { 28 if(o>=ans) return; //當前塗色次數大於等於當前答案,直接退出 29 if(pq==n) //塗完了,記錄答案 30 { 31 ans=o; 32 return; 33 } 34 for(int i=1;i<=m;i++) //枚舉顏色 35 { 36 int qq=0; //代表現在用這個顏色塗的磚數 37 if(i!=xx&&de[i])//如果有這個顏色,並且這種顏色上次沒用過 38 { 39 for(int j=1;j<=n;j++) //塗色 40 { 41 if(!b[j]&&a[j].x==i&&OK(j)) //如果沒塗過該磚,並且能塗 42 { 43 b[j]=1; 44 qq++; 45 } 46 else if(b[j]&&a[j].x==i) b[j]++; 47 } 48 if(qq>0) dfs(o+1,pq+qq,i); 如果塗了磚,進行下一步 49 for(int j=n;j>=1;j--) //回溯一步 50 { 51 if(b[j]==1&&a[j].x==i&&OK(j)) 52 { 53 b[j]=0; 54 qq--; 55 } 56 else if(b[j]>1&&a[j].x==i) b[j]--; 57 } 58 } 59 } 60 } 61 int main() 62 { 63 cin>>n; 64 for(int i=1;i<=n;i++) 65 { 66 scanf("%d%d%d%d%d",&a[i].a1,&a[i].b1,&a[i].a2,&a[i].b2,&a[i].x); 67 a[i].a1++; //個人習慣把左上角坐標+1,就可以看成它左上角所占的方格 68 a[i].b1++; // 例如 0 0 2 2 +1後為 1 1 2 2 ,表示該磚左上角,右下角所占的方格 69 de[a[i].x]++; //記錄顏色 70 } 71 for(int i=1;i<=20;i++) if(de[i]) m=i; //求最大顏色編號 72 sort(a+1,a+n+1,ccmp); //按左上角坐標大小從小到大排序(先考慮縱,再考慮橫) 73 for(int i=2;i<=n;i++) 74 for(int j=i-1;j>=1;j--) 75 if(a[i].a1==a[j].a2+1&& ( (a[i].b1>=a[j].b1&&a[i].b1<=a[j].b2) || (a[i].b2>=a[j].b1&&a[i].b2<=a[j].b2) ) ) 76 fk[i][j]=1; //如果i磚的最上面緊鄰j磚最下面,且兩磚橫坐標有重疊部分,即j磚為i磚緊鄰上面的磚 77 dfs(0,0,0); 78 cout<<ans;//結果 79 return 0; 80 }
3、
用二進制壓縮狀態,一個n位二進制數的第i位為0或1表示第i塊板是否圖上了色。
f[A][i]表示達到A狀態,最後一次塗色的顏色是i的最少換顏色次數。
位運算不懂的自己百度。
檢查二進制數A第i位是否為0: A&(1<<(i-1))==(1<<(i-1))
二進制數A的第i位上的1變為0後的數: A-(1<<(i-1))
詳見代碼:
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout) 4 int f[(1<<16)+1][21],n,color[20],b[100][100],maxcolor=0; 5 int num[20],temp[20][20],xx[20],xy[20],yx[20],yy[20],ans=INT_MAX; 6 bool check(int A,int x)//檢查A狀態下第x個矩形上方的所有矩形是否已經塗完色 7 { 8 bool flag=true; 9 for(int i=1;i<=num[x]&&flag;i++)//num[x]是第x個矩形上方相鄰的矩形個數,temp[x][i]是這些矩形的編號 10 if(((1<<(temp[x][i]-1))&A)!=(1<<(temp[x][i]-1)))flag=false;//如果上方某個矩形還未被塗色,則第x個矩形就不能塗色,就標記flag為false 11 return flag;//如果上方沒有矩形則num[x]==0,就不會進行循環,直接return ture 12 } 13 int main() 14 { 15 //file(paint); 16 memset(f,32,sizeof f);//初始化 17 scanf("%d",&n); 18 for(int i=1;i<=n;i++) 19 { 20 scanf("%d%d%d%d%d",&xx[i],&yx[i],&xy[i],&yy[i],&color[i]); 21 if(color[i]>maxcolor)maxcolor=color[i];//記錄顏色的個數,即最大顏色編號 22 for(int j=xx[i];j<xy[i];j++) 23 for(int k=yx[i];k<yy[i];k++) 24 b[j][k]=i;//b[i][j]表示第i行j列所在的矩形編號 25 } 26 for(int i=1;i<=n;i++) 27 { 28 int k=xx[i]-1;//掃一遍矩形上面一行,num[i]表示矩形i上方的不同矩形個數,temp[i][j]表示第i個矩形上方第j個矩形的編號。 29 if(k<0)continue; 30 for(int j=yx[i];j<yy[i];)//從左往右掃上方的矩形 31 if(b[k][j])//如果有矩形 32 { 33 int l=j; 34 while(b[k][l]==b[k][j]&&l<yy[i])l++;//跳過編號相同的矩形 35 temp[i][++num[i]]=b[k][j];//記錄上方的矩形編號 36 j=l;//繼續掃 37 } 38 } 39 for(int i=1;i<=maxcolor;i++) 40 f[0][i]=1;//初始化,所有平板未塗色時需要拿一次刷子。 41 for(int A=1;A<=((1<<n)-1);A++)//枚舉每個著色狀態,n塊平板的狀態用二進制表示就是0到(2^n-1),位運算優化 42 for(int i=1;i<=n;i++)//枚舉放第i塊平板 43 if(((1<<(i-1))&A)==(1<<(i-1))&&check(A,i))//檢查該狀態中是否已經塗上了第i個矩形,還有該狀態下第i個矩形的上方矩形是否都已塗完 44 {//狀態轉移: for(int j=1;j<=maxcolor;j++)//枚舉每種顏色 45 46 if(j!=color[i])f[A][color[i]]=min(f[A][color[i]],f[A-(1<<(i-1))][j]+1);//如果前驅狀態的顏色不同就要換刷子 47 48 f[A][color[i]]=min(f[A][color[i]],f[A-(1<<(i-1))][color[i]]);//顏色相同就不換刷子 49 50 } 51 for(int i=1;i<=maxcolor;i++) 52 ans=min(ans,f[(1<<n)-1][i]);//枚舉最後顏色不同的最終狀態,取最小值為結果 53 printf("%d\n",ans); 54 return 0; 55 }
P1283 平板塗色
