堆的實現

雖然我們之前的介紹堆的時候是一個二叉樹，但是我們實現堆的時候並不是按照傳統的二叉樹實現（傳統的二叉樹是用鏈的形式，即一個父節點存放兩個子節點的引用）

為什麽要這樣說呢？

我們先看一下堆的結構：

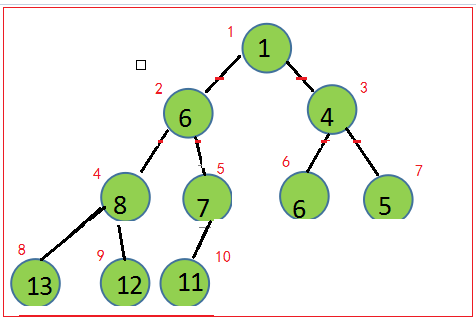
如果我們觀察每一個節點的順序，我們會發現一個有趣的規律：

對於任意個下標a的元素，他的左孩子下標是2*a,右孩子下標是2*a+1，父節點下標是a/2取整。

而堆又有分層添加（一層添加完才需要添加下一層）的特性，所以用數組來實現堆，才是一個最佳的選擇。

那麽如果是一個數組，堆的插入和取值如何實現呢？

插入：

上圖的堆如果轉換成數組就是下面這樣，紅色為數組下標：

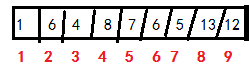
當要進行插入操作時，堆會把新值放到堆的最後，對數組來說就是數組的最後啦~實現起來很簡單！

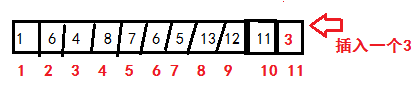
然後，我們需要判斷是否滿足條件：父元素比子元素小（我們按最小堆來解釋）。

3的下標是11，那麽根據上面的公式：每個節點的父節點下標是此節點下標/2取整，那麽他的父元素就是下標11/2=5，下標5對於的數字是7

由於7>3，所以需要替換

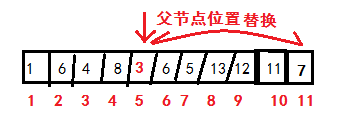
再次比較3的父節點(5/2=2,即第2個元素6)，發現比父節點小，依然替換

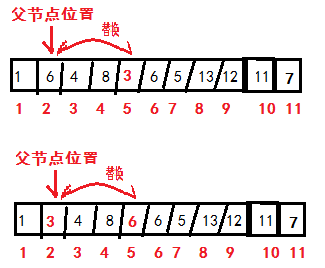
再次按上述規則比較，發現符合條件，插入完成！

取最小數：

由之前的內容可以知道，取最小數就是取第一個數，然後把最後一個數放到第一個數的位置，如下圖所示：

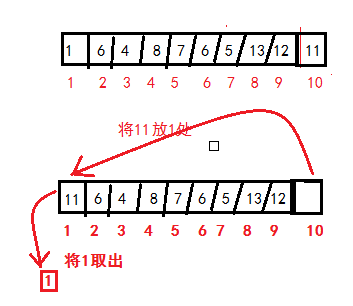
然後我們比較是否滿足條件：父元素小於兩個子元素

下標 1的兩個子節點下標分別為分別2（1*2）和3（1*2+1），對應值

下標1的對應值為11，大於4，不滿足條件，所以替換

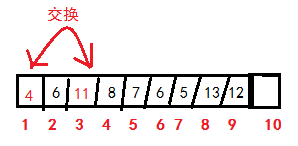
再次比較是否滿足條件：

下標3的兩個子節點下標為6（3*2）和7（3*2+1），對應值6和5

下標3對應值為11，大於5，不滿足條件，所以替換

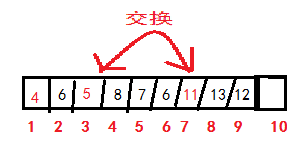
再次按上述規則比較，發現滿足條件，至此，取最小值完成；

堆的實現（圖片演示+文字講解）