線性近似

　　假設一般函數上存在點(x₀, f(x₀))，當x接近基點x₀時，可以使用函數在x₀點的切線作為函數的近似線。函數f(x)≈f(x₀)+f‘(x₀)(x- x₀)即稱為函數f在x₀點的線性近似或切線近似。

f(x) ≈ f(x₀) + f‘(x₀)(x- x₀)

公式來源

幾何意義

　　線性近似求解的是近似值，其幾何意義是在基點的切線近似於原函數的曲線。

　　以f(x)=lnx為例，根據公式，在x₀=1，lnx≈x-1，曲線和切線如下圖所示：

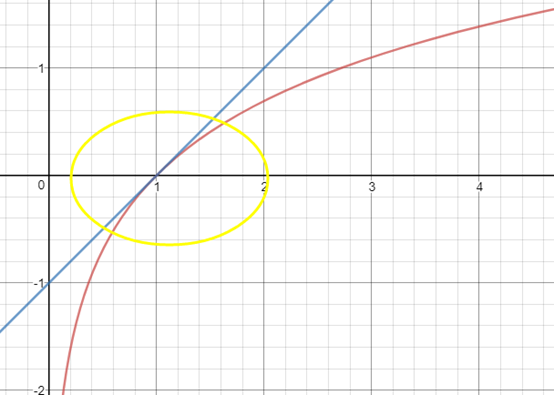
　　在x₀=1點附近，曲線近似於直線，x越接近x₀，二者的近似度越高。在討論近似時，只有指定基點才有意義。這很容易理解，x越遠離x₀，曲線和直線的差距越大；同時，當基點不同時，切線的斜率也不同。

常用線性近似

　　x₀=0　　

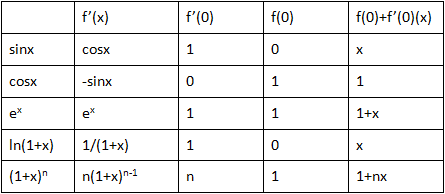
　　以下是上述線性近似的幾何意義：

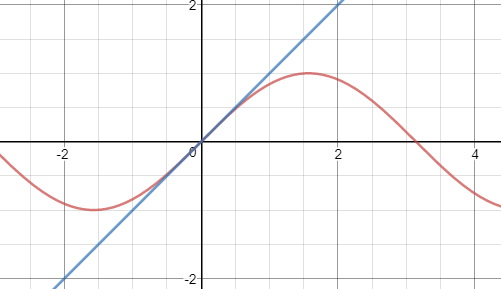
sinx≈x

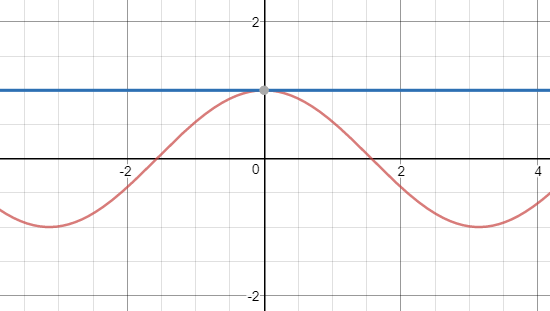
cosx≈1

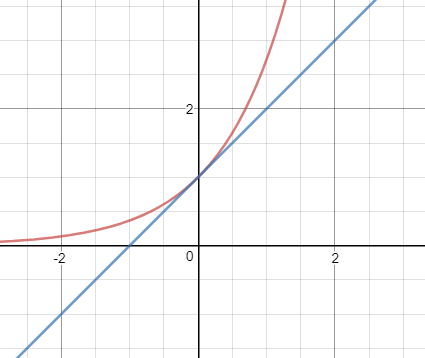
e^x≈x+1

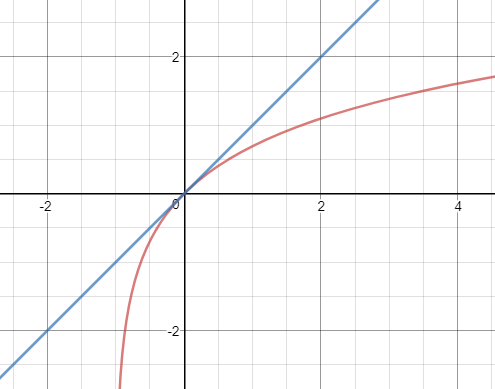
ln(x+1)≈x

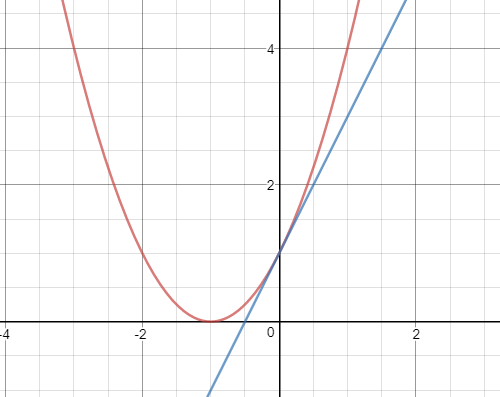
(1+x)ⁿ≈1+nx,n=2

化繁為簡

　　例1：ln(1.1) = ?

　　這需要計算器了，但實際工作中往往只需要尋找近似值。

　　如果設x=0.1，則 ln(1.1) = ln(1+x)，當x≈0時，ln(1+x) ≈ x，在此， 我們認為0.1接近於0，ln(1.1) = ln(1+x) ≈ x = 0.1

　　0.1是否接近於0，這是個及其主觀的判斷，要視具體問題而定。某些時候，0.1可能距離0很遠，另一些時候，10也可能距離0很近。

　　例2：在x≈0時，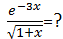

　　這不需要計算器，直接將代入x=0即可，結果為1，然而這種方法不總是有效，如果分母是1-x或x≈-1就不靈了。

　　還是使用線性近似的思路，首先需要把式子轉換成我們認識的寫法：

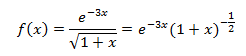
　　當x≈0時，根據公式f(x) ≈ f‘(0)(x) + f(0)，重點是計算f’(0)：

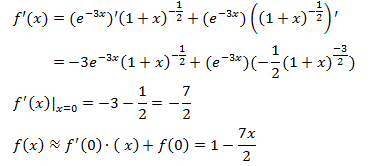
　　對這個長長的式子求導非常麻煩，涉及到多個求導法則，我們希望用簡單的方式求解。

　　對於本例來說，非常幸運，我們已經知道x≈0時 e^x≈1+x，xⁿ≈1+nx，代入本例：

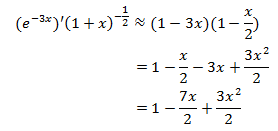
　　當x≈0時，高階函數3x²/2≈0，隨著x→0，3x²/2更快地趨近於0，所以上式可舍棄高階函數：

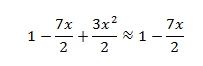
　　通過這兩個例子可以看出線性近似的作用——化繁為簡。等號左側的式子是繁，比如ln1.1和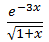，通過線性近似將其轉化為簡單的式子，0.1和1-7x/2

　　在轉換過程中當然會損失一些精度，但絕大多數時候我們都無需得到精確的解，例如在x=0.0001的時候，原式的計算量相當大，化簡後將極大地簡化計算，而付出的代價相當少，幾乎可以忽略；某些時候甚至根本無法得到精確解，比如無理數的計算。取而代之，我們求得可接受的近似解，通過近似解化繁為簡。

　　化繁為簡的思路也貫穿於整個數學，後續我們將看到，在求解復雜問題時，采取的方法幾乎都是不斷尋找近似、舍棄。

　　在利用計算機尋找最優解時，幾個常用的算法是爬山法、模擬退火算法、遺傳算法，這些算法都是采用化繁為簡的思路，舍棄全局最優解，尋找可以接受的較好解，故每次得到的結果都會稍有偏差。

二階近似

公式

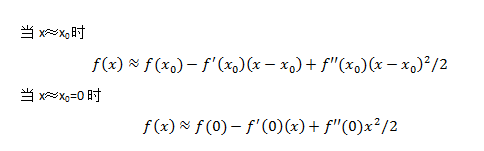
幾何意義

　　二階近似的幾何意義是最接近原函數的拋物線，它比線性近似更為精確。

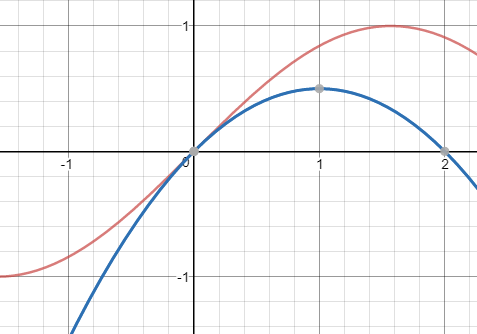
　　以f(x)=ln(1+x)為例，根據公式，在x₀=0，

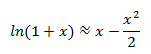
　　曲線如下：

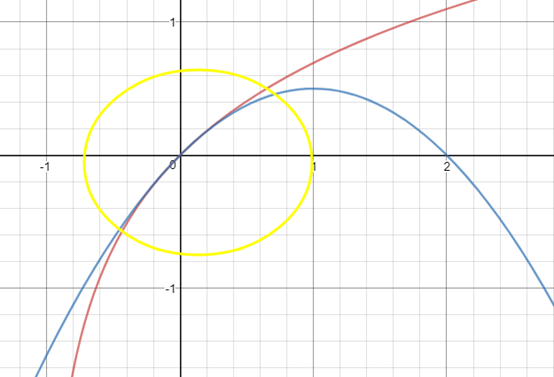
ln(1+x)≈x-x²/2

　　對比線性近似可以看出，二階近似在基點附近更貼近原函數。

常用二階近似

　　x₀=0

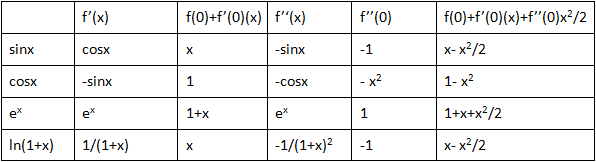
　　以下是上述線性近似的幾何意義：

sinx≈x-x²/2

cosx≈1-x²

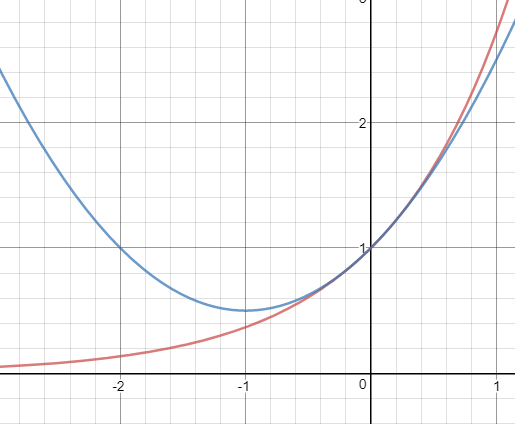
e^x≈1+x+x²/2

ln(1+x)≈x-x²/2

總結

作者：我是8位的

出處：http://www.cnblogs.com/bigmonkey

本文以學習、研究和分享為主，如需轉載，請聯系本人，標明作者和出處，非商業用途！

數學筆記6——線性近似和二階近似