希臘的哲學家芝諾曾經辯論說，一支箭永遠不能達到它的目標。他說，首先箭要到達目標距離的一半，然後又必須到達剩餘距離的一半，然後還有一半，這樣就沒有窮盡。因為這個旅程有無限個部分，所以箭要花費無限的時間才能結束這個旅程。這就是“芝諾悖論”。芝諾的結論是——時間是不存在的。儘管他自己也不相信這個結論。這個問題看似詭異，但在數學面前，神祕蕩然無存，破解問題的關鍵就是無窮級數。

悖論的謎底

　　把芝諾問題用數學表達就是：

　　更普遍的寫法是：

　　其實很早就有人揭開了悖論的謎底，先將等號兩邊同時乘以a：

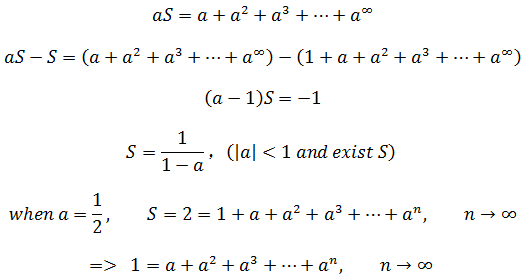
　　所以芝諾問題的最終答案是1。需要注意的是，只有當 -1 < a < 1時上述公式才成立，否則結果將是發散的。

無窮級數

　　對於和幾何級數類似的和式，用數學符號表示：

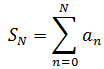
　　稱S_N為部分和，當N→∞時，和式就是無窮極限：

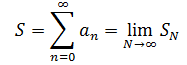
　　無窮極限S的結果可能是收斂的，有可能是發散的。

無窮級數的收斂性

　　我們感興趣的第一個問題是無窮級數的收斂性。

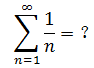
　　上式的收斂性沒有那麼明顯，應當如何判斷？

　　仔細觀察上式會發現，它和黎曼和及其類似，如果Δx =1，那麼

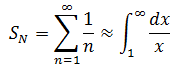
　　需要注意的的，二者接近但並不相等，積分處理的是當Δx→0的情況。

　　對於黎曼和，如果當Δx = 1時使用左矩形公式（數值積分可參考《數學筆記19——數值積分》），則：

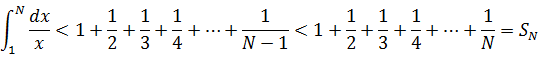
　　如果使用右矩形公式，則：

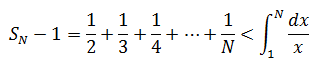
　　綜上：

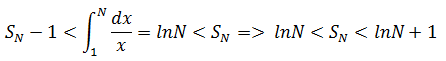
　　由於lnN是發散的，所以S_N也是發散的。

積分比較判別法

　　上面的例子展示了和式和積分的關係，這樣描述“積分比較法”：如果f(x)是減函式，且f(x) > 0，則：

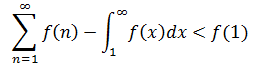
　　和式和積分的收斂性一致。

　　積分比較的基本思想就是用積分代替和式，因為和式通常很難計算，但和式對應的積分往往很容易，所以需要化繁為簡，這也是數學的基本思想。

極限比較判別法

　　與積分比較類似，如果f(x)等價於g(x)，即x→∞時f(x)/g(x) = 1，其中n > 0, f, g >，則∑f(x)和∑g(x)的收斂性一致。

比值判別法

　　當積分法和極限法出現困難時，比值法將是一個值得嘗試的方案，對於∑a_n，a_n > 0 來說，

　　如果L < 1，∑a_n是收斂的；如果L > 1∑a_n

示例

　　判斷下面三個式子的收斂性：

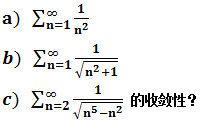
　　a.使用積分判別法

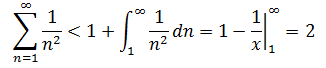
　　答案是收斂的，最終結果≈2

　　該求解過程也可以推廣到f(x) = 1/n^m

　　b.使用極限比較判別法

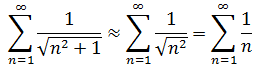
　　結果是發散的。

　　c.使用極限比較判別法

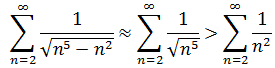
　　結果是收斂的。

綜合示例

示例1

　　判斷下面三個式子的收斂性：

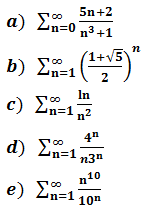
　　a.使用極限比較判別法

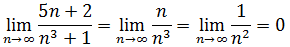
　　答案是收斂。

　　b.

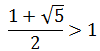
　　題目是幾何級數，答案是發散。

　　c.使用極限比較判別法

　　lnn << n，lnn/n² << 1/n，所以結果是收斂。

　　d.使用比值判別法

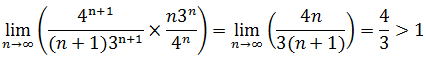
　　答案是發散。

　　e.使用比值判別法

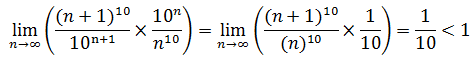
　　答案是收斂的。

示例2

　　判斷下面式子的收斂性：

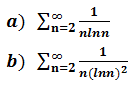
　　a.使用積分判別法，

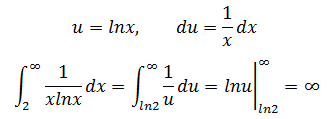
　　答案是發散

　　b.使用積分判別法，

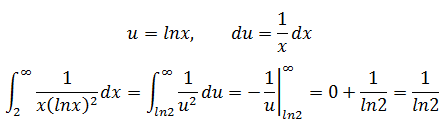
　　答案是收斂的。

 　　作者：我是8位的

　　出處：http://www.cnblogs.com/bigmonkey

　　本文以學習、研究和分享為主，如需轉載，請聯絡本人，標明作者和出處，非商業用途！