強連通分量-----Kosaraju
阿新 • • 發佈:2017-09-14
define can size scan true 其他 algo 模板 找到
芝士:
有向圖強連通分量在有向圖G中,如果兩個頂點vi,vj間(vi>vj)有一條從vi到vj的有向路徑,同時還有一條從vj到vi的有向路徑,則稱兩個頂點強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通,稱G是一個強連通圖。有向圖的極大強連通子圖,稱為強連通分量。
如圖中1,2,3,4是一個強連通分量。
Kosaraju算法:
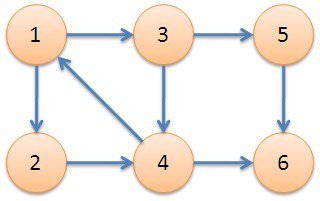
如果這是一個無向圖,那麽從一個節點出發,深搜得到的所有節點都是連通的。
但這是一個有向圖,起始節點的不同會導致結果的不同,舉個栗子,從5搜可以搜到6,但是從6搜不能搜到5。
這說明需要按照一個特定的順序深搜。假設1,2,3,4是強連通分量a,5,6分別是強連通分量b,c。a可以搜到b,c,但b,c不能搜到a,由於我們不希望搜到不屬於同一個強連通分量的點,所以會先搜b,c,再搜a。
那麽這個順序就是被指向的強連通分量要在指向的強連通分量之前被搜到,即被指向的強連通分量中的至少一個點在指向的強連通分量的任意一個點之前被搜到。
為了得到這個順序,聰明的Kosaraju想到了一個方法:新建原圖G的逆圖GT(其定義為GT=(V,ET),ET={(u,v):(v,u)∈E}}),按照節點編號順序在GT上深搜,每搜到一個節點,先把這個節點所能到達的所有未被訪問過的節點加入棧中,再把自己加入棧中,然後按照從棧頂到棧底的順序深搜,這樣保證了在原圖G中能到達我的點,都在我之後被搜到;
最後原圖中強連通分量的個數就等於深搜的次數,每一次深搜到達的未被訪問過的節點屬於一個強連通分量(可以用一個數組記錄一下);
模板:
/*
約翰的N (2 <= N <= 10,000)只奶牛非常興奮,因為這是舞會之夜!她們穿上禮服和新鞋子,別 上鮮花,她們要表演圓舞.
只有奶牛才能表演這種圓舞.圓舞需要一些繩索和一個圓形的水池.奶牛們圍在池邊站好, 順時針順序由1到N編號.每只奶牛都面對水池,這樣她就能看到其他的每一只奶牛.
為了跳這種圓舞,她們找了 M(2<M< 50000)條繩索.若幹只奶牛的蹄上握著繩索的一端, 繩索沿順時針方繞過水池,另一端則捆在另一些奶牛身上.這樣,一些奶牛就可以牽引另一些奶 牛.有的奶牛可能握有很多繩索,也有的奶牛可能一條繩索都沒有.
對於一只奶牛,比如說貝茜,她的圓舞跳得是否成功,可以這樣檢驗:沿著她牽引的繩索, 找到她牽引的奶牛,再沿著這只奶牛牽引的繩索,又找到一只被牽引的奶牛,如此下去,若最終 能回到貝茜,則她的圓舞跳得成功,因為這一個環上的奶牛可以逆時針牽引而跳起旋轉的圓舞. 如果這樣的檢驗無法完成,那她的圓舞是不成功的.
如果兩只成功跳圓舞的奶牛有繩索相連,那她們可以同屬一個組合.
給出每一條繩索的描述,請找出,成功跳了圓舞的奶牛有多少個組合?
輸入n,m,接下來m行
*/
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define nn 10010
#define mm 100010
using namespace std;
int e=0,l=0,ee=0,cir;
int nx[mm],fi[nn],too[mm];
int fir[nn],nxt[mm],to[mm],li[nn];
bool vis[nn];
void add(int u,int v)
{
nxt[++e]=fir[u];fir[u]=e;to[e]=v;
}
void add2(int u,int v)
{
nx[++ee]=fi[u];fi[u]=e;too[e]=v;
}
void dfs(int s)
{
vis[s]=1;
for(int i=fi[s];i;i=nx[i])
{
if(!vis[too[i]])
dfs(too[i]);
}
li[++l]=s;
}
void dfs2(int s)
{
vis[s]=1;cir++;
for(int i=fir[s];i;i=nxt[i])
{
if(!vis[to[i]])
dfs2(to[i]); //寫成了dfs
}
}
int main()
{
int n,m,u,v,ma=-1,sum=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add(u,v);
add2(v,u);
}
for(int i=1;i<=n;i++)
if(!vis[i])
dfs(i);
fill(vis,vis+n+1,0);
for(int i=l;i>=1;i--)
if(!vis[li[i]]) //寫成了vis[i]
{
cir=0;
dfs2(li[i]);
if(cir>=2) sum++;
}
printf("%d",sum);
return 0;
}
強連通分量-----Kosaraju
