9.17模擬賽
T1 巧克力棒
題目描述
LYK 找到了一根巧克力棒,但是這根巧克力棒太長了,LYK 無法一口吞進去。
具體地,這根巧克力棒長為nn,它想將這根巧克力棒折成nn段長為11的巧克力棒,然後慢慢享用。
它打算每次將一根長為kk的巧克力棒折成兩段長為aa和bb的巧克力棒,此時若a=ba=b,則LYK 覺得它完成了一件非常困難的事,並會得到11點成就感。
LYK 想知道一根長度為nn的巧克力棒能使它得到最多幾點成就感。
輸入輸出格式
輸入格式:
第一行一個數nn。
輸出格式:
一個數表示答案。
輸入輸出樣例
輸入樣例#1:7
輸出樣例#1:4
說明
對於20\%20%的數據,n \leq 5n≤5。
對於50\%50%的數據,n \leq 20n≤20。
對於80\%80%的數據,n \leq 2000n≤2000。
對於100\%100%的數據,n \leq 1000000000n≤1000000000。
樣例解釋
將77掰成3+43+4, 將33掰成1+21+2, 將44掰成2+22+2獲得11點成就感, 將剩下的所有22掰成 1+11+1
獲得33點成就感。總共44點成就感。
題解:
考試80分dp,計算局部最優值 枚舉斷點取最大
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n,f[2017]; intmain(){ freopen("chocolate.in","r",stdin); freopen("chocolate.out","w",stdout); scanf("%d",&n); f[1]=0;f[2]=1;f[3]=1; for(int i=4;i<=n;i++){ for(int j=0;j<=i;j++){ f[i]=max(f[i],f[j]+f[i-j]); } if(i%2==0)f[i]=max(f[i],f[i/2]*2+1); } printf("%d\n",f[n]); fclose(stdin); fclose(stdout); return 0; }
正解:貪心
發現最後肯定分成n個長度為1,要求有貢獻,那麽長度為1的一定是由長度為2的分來的,分成長度為2 想要有貢獻 必須從長度為4分來的,分成
長度為4想要有貢獻 必須分成長度為8的.....所以將巧克力棒分成2^k得到的結果更優。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; long long n,ans,js; void dfs(long long n){ if(n==1||n==0)return; long long i; for( i=1;i*2<=n;i*=2); ans+=i-1; dfs(n-i); } int main(){ scanf("%lld",&n); dfs(n); cout<<ans<<endl; return 0; }
T2 LYK 快跑!
題目描述
LYK 陷進了一個迷宮! 這個迷宮是網格圖形狀的。 LYK 一開始在(1,1)(1,1)位置, 出口在(n,m)(n,m)。
而且這個迷宮裏有很多怪獸,若第aa行第bb列有一個怪獸,且此時 LYK 處於第 cc行dd列,此時這個怪獸對它的威脅程度為|a-c|+|b-d|∣a?c∣+∣b?d∣。 LYK 想找到一條路徑,使得它能從(1,1)(1,1)到達(n,m)(n,m),且在途中對它威脅程度最小的怪獸的威脅程度盡可能大。
當然若起點或者終點處有怪獸時,無論路徑長什麽樣,威脅程度最小的怪獸始終=0=0。
輸入輸出格式
輸入格式:
第一行兩個數n,mn,m。
接下來nn行,每行mm個數,如果該數為00,則表示該位置沒有怪獸,否則存在怪獸。
數據保證至少存在一個怪獸。
輸出格式:
一個數表示答案。
輸入輸出樣例
輸入樣例#1:3 4
0 1 1 0
0 0 0 0
1 1 1 0
輸出樣例#1:1
說明
對於20\%20%的數據n=1n=1。
對於40\%40%的數據n \leq 2n≤2。
對於60\%60%的數據n,m \leq 10n,m≤10。
對於80\%80%的數據n,m \leq100n,m≤100。
對於90\%90%的數據n,m \leq 1000n,m≤1000。
對於另外10\%10%的數據n,m \leq 1000n,m≤1000且怪獸數量\leq 100≤100。
題目大意:要求從(1,1)-->(n,m)的路徑中距離最小的怪獸的距離最大值
題解:題目描述最小值最大應該是二分...可是我沒想出來...
40搜索....(吐槽:只有40分不該呀.....
#include<iostream> #include<cstdio> #include<queue> #include<algorithm> #include<cstring> using namespace std; int n,m,cnt,ans,js; int map[102][102],vis[102][102]; int mx[4]={0,1,0,-1}, my[4]={1,0,-1,0}; struct WW{ int x,y; }w[10005]; struct T{ int x,y,minl; }s[50003]; int zs(int x){ if(x<0)return -x; return x; } void slove(){ queue<T>q;T s;s.x=1;s.y=1;s.minl=0x7fffffff; q.push(s); while(!q.empty()){ T now; now=q.front();q.pop(); vis[now.x][now.y]=0; int minl=0x7ffffff; for(int i=1;i<=cnt;i++){ int xx=w[i].x,yy=w[i].y; minl=min(minl,zs(xx-now.x)+zs(yy-now.y)); } if(minl<now.minl)now.minl=minl;js++; cout<<now.x<<" "<<now.y<<" "<<now.minl<<endl; if(js==10){ exit(0); } if(now.x==n&&now.y==m)ans=max(ans,now.minl); for(int i=0;i<4;i++){ int xx=now.x+mx[i],yy=now.y+my[i]; if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!vis[xx][yy]){ vis[xx][yy]=1; q.push((T){xx,yy,now.minl}); } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ int x; scanf("%d",&x); if(x)w[++cnt].x=i,w[cnt].y=j; if((i==1&&j==1&&x)||(i==n&&j==m&&x)||n==1){ printf("0\n"); return 0; } } } slove(); printf("%d\n",ans); return 0; }
正解:bfs預處理到每個非怪獸節點的最近的怪獸的距離,然後二分答案。
隊列要開大點
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n,m,l,r,ans,map[1002][1002],vis[1002][1002],qx[1000000],qy[1000000],b[1002][1002]; int mx[4]={0,1,-1,0}, my[4]={1,0,0,-1}; int head=1,tail; bool check(int limt){ memset(vis,0,sizeof(vis)); memset(qx,0,sizeof(qx)); memset(qy,0,sizeof(qy)); head=1;tail=0; qx[++tail]=1;qy[tail]=1;vis[1][1]=1; while(head<=tail){ int nowx=qx[head],nowy=qy[head++]; for(int i=0;i<4;i++){ int xx=nowx+mx[i],yy=nowy+my[i]; if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!vis[xx][yy]&&b[xx][yy]>=limt){ qx[++tail]=xx;qy[tail]=yy; vis[xx][yy]=1; } } } return vis[n][m]; } void bfs(){ while(head<=tail){ int nowx=qx[head],nowy=qy[head++]; for(int i=0;i<4;i++){ int xx=nowx+mx[i],yy=nowy+my[i]; if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!vis[xx][yy]&&!b[xx][yy]&&!map[xx][yy]){ b[xx][yy]=b[nowx][nowy]+1; vis[xx][yy]=1; qx[++tail]=xx;qy[tail]=yy; } } } l=0;r=n*m; while(l<=r){ int mid=(l+r)>>1; if(check(mid)){ ans=mid;l=mid+1; } else r=mid-1; } printf("%d\n",ans); } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ scanf("%d",&map[i][j]); if(map[i][j]){ qx[++tail]=i; qy[tail]=j; } } } if(map[1][1]||map[n][m]||n==1){ printf("0\n"); return 0; } bfs(); return 0; }
T3 仙人掌(cactus)
題目描述
LYK 在沖刺清華集訓(THUSC)於是它開始研究仙人掌,它想來和你一起分享它最近研究的結果。
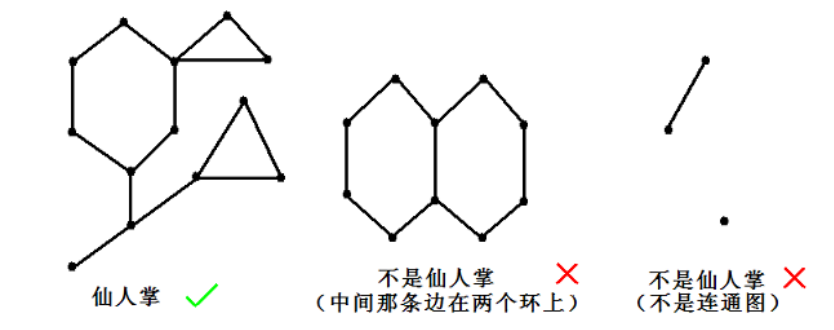
如果在一個無向連通圖中任意一條邊至多屬於一個簡單環 (簡單環的定義為每個點至多經過一次) ,且不存在自環,我們稱這個圖為仙人掌。
LYK 覺得仙人掌還是太簡單了,於是它定義了屬於自己的仙人掌。
定義一張圖為美妙的仙人掌, 當且僅當這張圖是一個仙人掌且對於任意兩個不同的點i,ji,j,存在一條從ii出發到jj的路徑,且經過的點的個數為|j-i|+1∣j?i∣+1個。 給定一張nn個點mm條邊且沒有自環的圖,LYK 想知道美妙的仙人掌最多有多少條邊。
數據保證整張圖至少存在一個美妙的仙人掌。
輸入輸出格式
輸入格式:
第一行兩個數n,mn,m表示這張圖的點數和邊數。
接下來mm行,每行兩個數u,vu,v表示存在一條連接u,vu,v的無向邊。
輸出格式:
一個數表示答案
輸入輸出樣例
輸入樣例#1:4 6
1 2
1 3
1 4
2 3
2 4
3 4
輸出樣例#1:4
說明
對於20\%20%的數據n \leq 3n≤3。
對於40\%40%的數據n \leq 5n≤5。
對於60\%60%的數據n \leq 8n≤8。
對於80\%80%的數據n \leq 1000n≤1000。
對於100\%100%的數據n \leq 100000n≤100000且m \leq min(200000,n*(n-1)/2)m≤min(200000,n?(n?1)/2)。
樣例解釋
選擇邊1-21?2,1-31?3,2-32?3,3-43?4,能組成美妙的仙人掌,且不存在其它美妙仙人掌有超過44條邊。
題解:30騙分(就問你強不強...
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n; int main(){ freopen("cactus.in","r",stdin); freopen("cactus.out","w",stdout); scanf("%d",&n); printf("%d\n",n); fclose(stdin); fclose(stdout); return 0; }
正解:由於i--j滿足節點數等於|i-j|+1,那麽i和i+1一定由一條邊直接連著,剩下的邊用線段覆蓋解決。
#include<cstdio> #include<algorithm> #define maxn 100010 using namespace std; int n,m,cnt; struct node{ int u,v; bool operator < (const node &x)const{ return v<x.v; } }e[maxn*2]; int init(){ int x=0,f=1;char s=getchar(); while(s<‘0‘||s>‘9‘){if(s==‘-‘)f=-1;s=getchar();} while(s>=‘0‘&&s<=‘9‘){x=x*10+s-‘0‘;s=getchar();} return x*f; } int main() { freopen("cactus.in","r",stdin); freopen("cactus.out","w",stdout); n=init();m=init(); int u,v; for(int i=1;i<=m;i++){ u=init();v=init(); if(u>v)swap(u,v); if(u!=v-1){ e[++cnt].u=u;e[cnt].v=v; } } sort(e+1,e+1+cnt); int r=0,sum=0; for(int i=1;i<=cnt;i++) if(e[i].u>=r){ sum++;r=e[i].v; } printf("%d\n",sum+n-1); return 0; }
9.17模擬賽
