常用矩陣導數公式
1 矩陣\(Y=f(x)\)對標量x求導
矩陣Y是一個\(m\times n\)的矩陣,對標量x求導,相當於矩陣中每個元素對x求導
\[\frac{dY}{dx}=\begin{bmatrix}\dfrac{df_{11}(x)}{dx} & \ldots & \dfrac{df_{1n}(x)}{dx} \\ \vdots & \ddots &\vdots \\ \dfrac{df_{m1}(x)}{dx} & \ldots & \dfrac{df_{mn}(x)}{dx} \end{bmatrix}\]
2 標量y=f(x)對矩陣X求導
註意與上面不同,這次括號內是求偏導,\(X\)是是一個\(m\times n\)的矩陣,函數\(y=f(x)\)對矩陣\(X\)中的每個元素求偏導,對\(m\times n\)矩陣求導後還是\(m\times n\)矩陣
\[\frac{dy}{dX} = \begin{bmatrix}\dfrac{\partial f}{\partial x_{11}} & \ldots & \dfrac{\partial f}{\partial x_{1n}}\\ \vdots & \ddots & \vdots \\\dfrac{\partial f}{\partial x_{m1}} & \ldots & \dfrac{\partial f}{\partial x_{mn}}\end{bmatrix}\]
3 函數矩陣Y對矩陣X求導
矩陣\(Y=F(x)\)對每一個\(X\)的元素求導,構成一個超級矩陣
\[F(x)=\begin{bmatrix}f_{11}(x) & \ldots & f_{1n}(x)\\ \vdots & \ddots &\vdots \\ f_{m1}(x) & \ldots & f_{mn}(x) \end{bmatrix}\]
\[X=\begin{bmatrix}x_{11} & \ldots & x_{1s}\\ \vdots & \ddots &\vdots \\ x_{r1} & \ldots & x_{rs}\end{bmatrix}\]
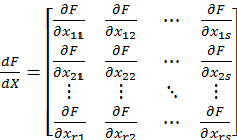 ,其中
,其中![clip_image002[4] 技術分享](http://images2017.cnblogs.com/blog/361409/201709/361409-20170924194834509-540541069.gif)
\[\frac{dF}{dX} = \begin{bmatrix}\dfrac{\partial F}{\partial x_{11}} & \ldots & \dfrac{\partial F}{\partial x_{1s}}\\ \vdots & \ddots & \vdots \\\dfrac{\partial F}{\partial x_{r1}} & \ldots & \dfrac{\partial F}{\partial x_{rs}}\end{bmatrix}\]
其中
\[\frac{\partial F}{\partial x_{ij}} = \begin{bmatrix}\dfrac{\partial f_{11}}{\partial x_{ij}} & \ldots & \dfrac{\partial f_{1n}}{\partial x_{ij}}\\ \vdots & \ddots & \vdots \\\dfrac{\partial f_{m1}}{\partial x_{ij}} & \ldots & \dfrac{\partial f_{mn}}{\partial x_{ij}}\end{bmatrix}\]
\[\frac{\partial F}{\partial x_{ij}} = \begin{bmatrix} \end{bmatrix}\]
重要結論:假設![]() 是一個向量:
是一個向量:
![]() ,
,![]() ,
,![]()
常用矩陣導數公式
