小x的質數

題目描述

小 X 是一位熱愛數學的男孩子，在茫茫的數字中，他對質數更有一種獨特的情感。小 X 認為，質數是一切自然數起源的地方。

在小 X 的認知裏，質數是除了本身和 11 以外，沒有其他因數的數字。

但由於小 X 對質數的熱愛超乎尋常，所以小 X 同樣喜歡那些雖然不是質數，但卻是由兩個質數相乘得來的數。

於是，我們定義，一個數是小 X 喜歡的數，當且僅當其是一個質數，或是兩個質數的乘積。

而現在，小 X 想要知道，在 LL 到 RR 之間，有多少數是他喜歡的數呢？

輸入格式

第一行輸入一個正整數 QQ，表示詢問的組數。

接下來 QQ 行。包含兩個正整數 LL 和 RR。保證 L \le RL≤R。

輸出格式

輸出 QQ 行，每行一個整數，表示小 X 喜歡的數的個數。

數據範圍與約定

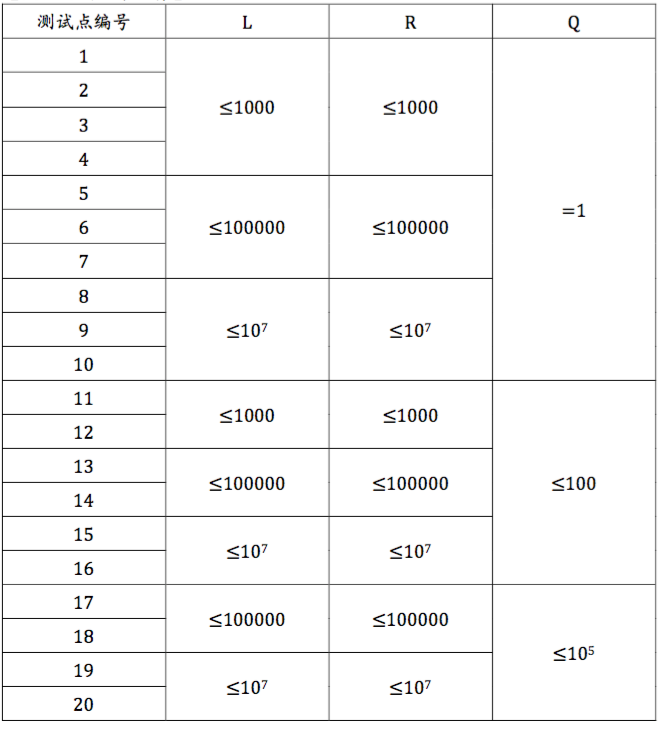
樣例

樣例解釋 1

66 以內的質數有 2,3,52,3,5，而 4=2 * 2,6 = 2 * 34=2∗2,6=2∗3。因此 2,3,4,5,62,3,4,5,6 都是小 X 喜 歡的數，而 1 不是。

樣例輸入1

1
1 6

樣例輸出1

5

樣例輸入2

10
282 491
31 178
645 856
227 367
267 487
474 697
219 468
582 792
315 612
249 307

樣例輸出2

97
78
92
65
102
98
114
90
133
29

樣例輸入3

10
20513 96703
15236 86198
23185 78205
40687 48854
42390 95450
63915 76000
36793 92543
35347 53901
44188 76922
82177 90900

樣例輸出3

24413
23001
17784
2669
16785
3833
17712
6028
10442
2734

code

 1 #include<cstdio>
 2
 
 #include<cmath>
 3 const int MAXN = 10000100;
 4 bool lk[MAXN],noprime[MAXN];
 5 int prime[MAXN];
 6 int sum[MAXN];
 7 
 8 int read() {
 9     int x = 0,f = 1;char ch = getchar();
10     for (; ch<‘0‘||ch>‘9‘; ch = getchar())
11         if (ch==‘-‘) f = -1;
12     for (; ch>=‘0‘&&ch<=‘9‘; ch = getchar())
13         x = x*10+ch-‘0‘;
14     return x*f;
15 }
16 
17 
18 
19 int main() {
20     
21     int tot = 0;
22     
23     for (int i=2; i<=10000000; i++) {
24         if (!noprime[i]) {
25             prime[++tot]=i;
26             lk[i] = true;
27             for (int j=1; j<=tot && i*prime[j]<=10000000; j++) {
28                 noprime[i*prime[j]] = true;
29                 lk[i*prime[j]] = true;
30             }
31         }
32         else {
33             for (int j=1; j<=tot&&i*prime[j]<=10000000; j++) {
34                 noprime[i*prime[j]] = true;
35                 if(i % prime[j] == 0) break ;  
36             }
37         }
38     }
39     for (int i=1; i<=10000000; ++i) {
40         if (lk[i]) sum[i] = sum[i-1]+1;
41         else sum[i] = sum[i-1];
42     }
43     
44     int L,R,q = read();
45     while (q--) {
46         L = read();R = read();
47         printf("%d\n",sum[R]-sum[L-1]);
48     }
49     
50     return 0;
51 }

小x的質數（線性O（n）篩素數）