本文作者frankchenfu，blogs網址http://www.cnblogs.com/frankchenfu/，轉載請保留此文字。

在數學上，圖是表示物件與物件之間聯系的數學對象；而在計算機中，每個物件可以抽象成一個節點，而關系就是一條邊。

這裏主要介紹圖的一些較關鍵的性質以及鄰接矩陣、鄰接表的應用。

1、有向圖和無向圖

圖分為有向圖和無向圖。顧名思義，有向圖就是每條邊都具有方向，一條從$A$->$B$的有向邊它可以讓一個東西從$A$走到$B$，卻不能沿同一條邊從$B$走回$A$；反之，無向圖就是不具有方向的，既可以從$A$到$B$，也可以沿同一條邊從$B$到$A$。一條邊可能有一個權值，叫邊權。

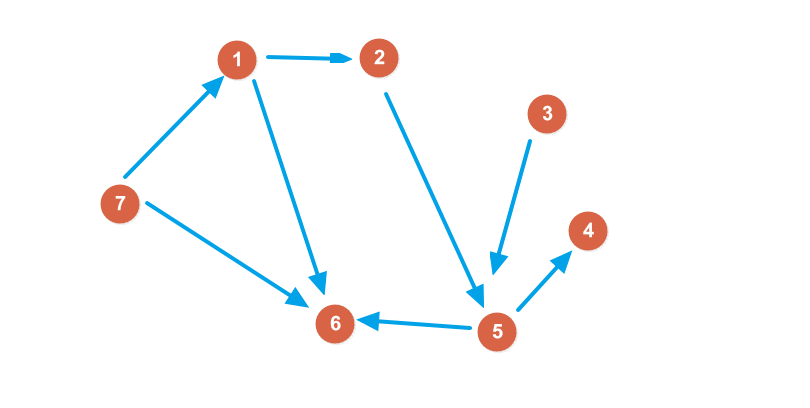
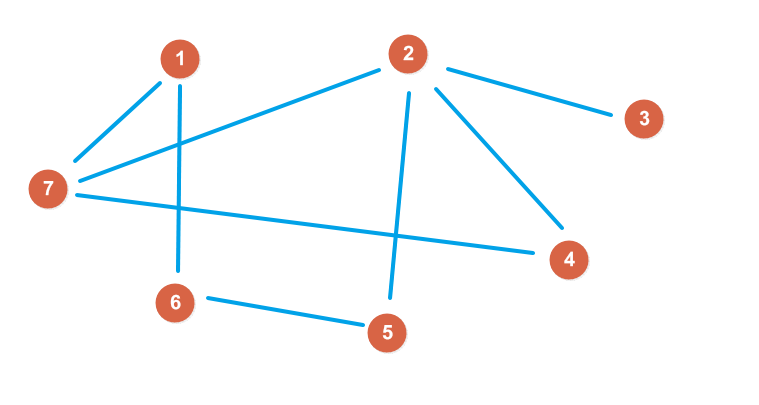
　　　　　　　　　　　有向圖　　　　　　　　　　　　　　　　　　　　　　　　　　　　　無向圖

註意到上面這一句話中，我強調了同一條邊。這表明，一張圖中可能會有重復的邊，即起點和終點相同的邊（在無向圖中可能是起點終點位置調換的邊），我們把這樣的邊成為重邊。

如果一張圖中，有$n$個結點，同時還有著$n-1$條邊，那麽這張圖事實上是一顆樹。

如果這張圖中，從$A$一直沿著某些不重復的邊走，然後能走回$A$，那麽這張圖中就存在著環。一張圖中可能存在著很多個環，也可能一個都沒有。例如，在上面的有向圖中，不存在環，而在無向圖中，結點$2,4,7$構成了一個環。

2、圖的存儲

限於篇幅，這裏僅介紹最常用的鄰接矩陣和鄰接表

2.1 鄰接矩陣法

我們可以構造一個矩陣，矩陣的第$i$行第$j$列（即$g_{i,j}$）表示結點$i$和結點$j$的關系，而沒有連邊的兩個節點，我們就設置為“假想無窮大”。例如，上面的有向圖可以表示為（inf即“假想無窮大”）：

這裏為第$i$行第$j$列為1表示有連邊。大家可以自行驗證是否表示上述有向圖。用代碼表示就可以是 g[i][j]=1; .無向圖也可以類似的表示，註意，因為邊是無向的，所以一旦第$i$行第$j$列有連邊，那麽第$j$行第$i$列也一定是有連邊的。用代碼表示即為 g[i][j]=g[j][i]=1; 。那麽鄰接矩陣法就講完了。可是，如果對於這樣一個數據範圍：

對於$100$%的數據滿足$n \le 10^6 , m \le 10^6$，其中$n$表示節點數，$m$表示邊數。

如果空間限制是標準的256MB或512MB，即使是1GB，存鄰接矩陣也是不夠的啊！鄰接矩陣的二維數組的空間消耗是O($n^2$)的。註意到有很多無用的空間，也就是上面的inf，事實上比我們有用的空間還多（在瀏覽上面的表格時你有沒有這麽想呢？）。因為邊的數量較小，於是我們考慮，能不能主要存邊的信息，而盡量不存點呢？於是我們的鄰接表就出來了。

2.2 鄰接表法

鄰接表的思想就是存邊的信息，而不是點的信息。我們給每一條邊一個編號。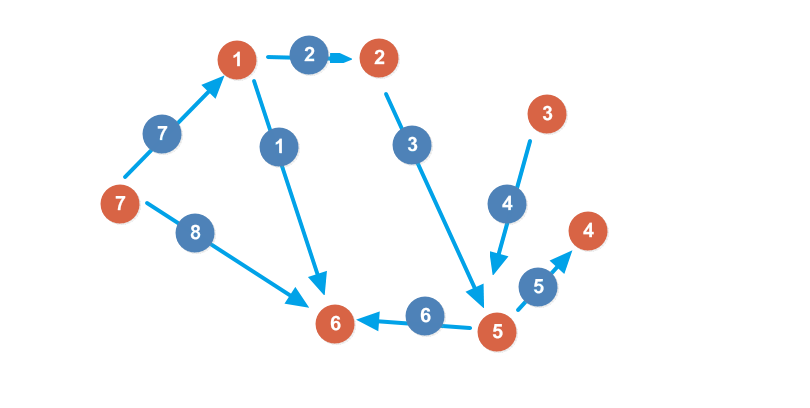

仍然對於上面的有向圖，我們鄰接表裏存的內容可以這麽表示：（其中冒號前的數字表示表示這一條邊的編號）

鄰接表存的就是這麽一個東西。它首先每個節點都有存一個“從這條邊出發的第一條邊”，然後每一條邊除了保存自身的信息（包括到哪裏去，權值等）以外，還有指向下一條邊的編號。這讓我們想起了什麽？對，鏈表！它每個節點內存的內容就很像鏈表，然後下一條邊指向0就表示結束了，這個節點的邊就遍歷忘了。這樣也是可以存儲一個圖的。這種方法的優點就是空間復雜度上的優勢，它的空間復雜度（如果不考慮每個節點存的“第一條邊”的話）是O($m$)的。那麽對於上面的數據範圍就可以很輕松的解決了。

可是這種方法也有缺點，例如判斷點之間是否聯通，那麽查找最壞情況下要O($m$)的復雜度，而鄰接矩陣只需要O($1$)。

接下來給出兩種存圖方法的Cpp代碼：

#include<cstdio>
#include<cstring>
//鄰接矩陣
const int MAXN=3010;
int g[MAXN][MAXN];//graph
int n,m;

//在一般情況下，u和v分別表示邊的起點和終點，w表示權值
void init()
{
    memset(g,0x7f,sizeof(g));//inf
    for(int i=1;i<=n;i++)
        g[i][i]=0;
}
void adde(int u,int v,int w)
{
    g[u][v]=w;//有向
    g[u][v]=g[v][u]=w;//無向
}

#include<cstdio>
#include<cstring>
//鄰接表
const int MAXN=100010;
const int MAXM=200010;//註意，無向圖空間雙倍!

struct edge
{
    int to,w,nxt;
}e[MAXM];
int fir[MAXN];
int n,m,tot=0;

void adde(int u,int v,int w)
{
    e[++tot].to=v;e[tot].w=w;
    e[tot].nxt=fir[u];
    fir[u]=tot;
}

打一個廣告，我自己的博客中還有使用鄰接表儲存的堆優化Dijkstra算法，有興趣的同學可以瀏覽一下。限於水平，作者所寫的難免有疏忽之處，望大家指正，Thanks！

圖論3——圖的存儲與基本性質