(輪廓線dp)UVA11270-Tiling Dominoes:

　　題意:

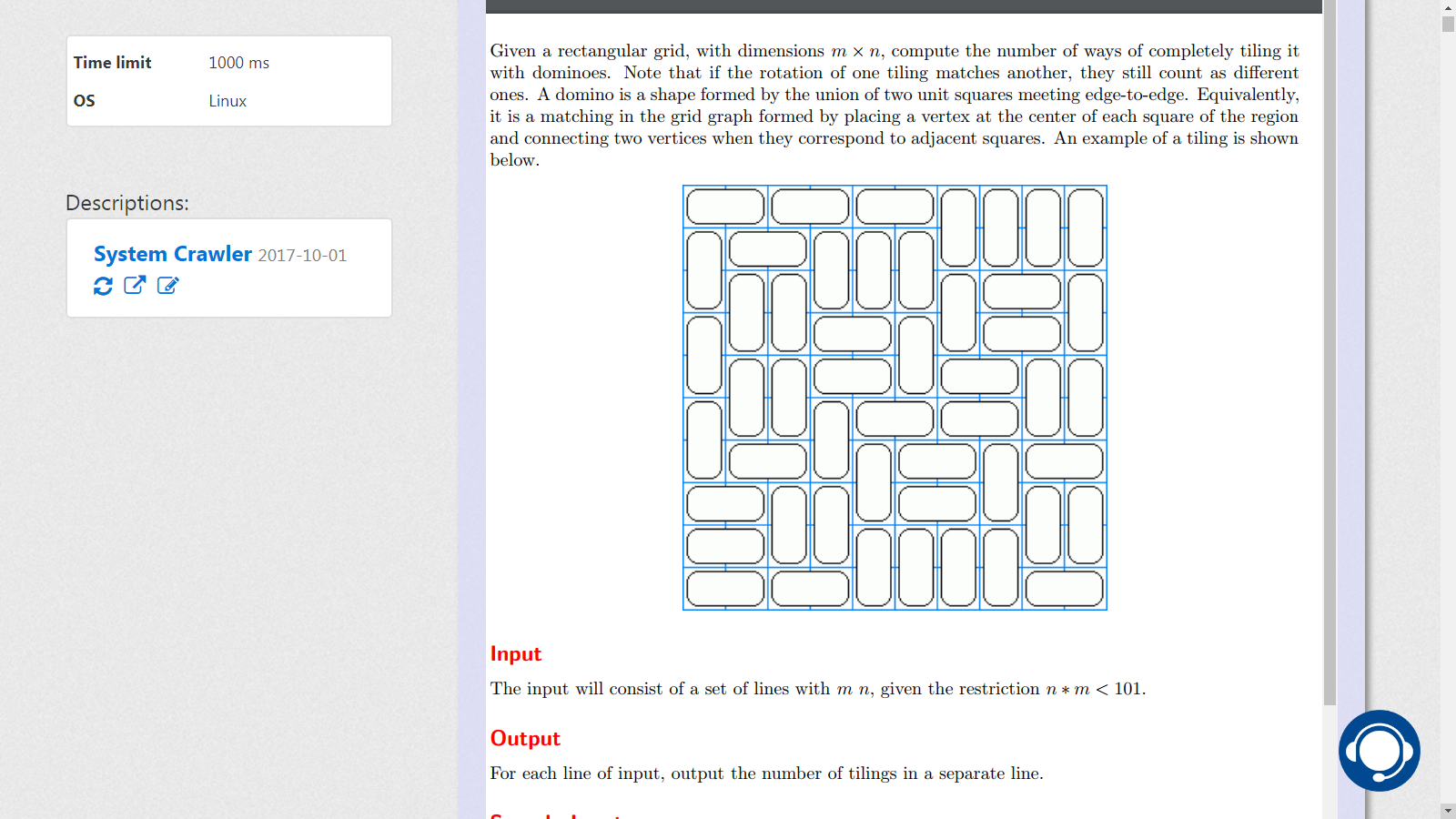
　　題解:

　　　　輪廓線dp.對著lrj書上的題解寫的.如果將所有格子從左到右,從上到下按順序排列,則可以dp,f[i][j][k]表示對於第i行第j列的格子前m個格子的狀態為k的種類數.

　　　　那麽轉移有3種情況:

　　　　1.不放,必須保證當前格子上方的那一個格子不為0,否則會有空位.

　　　　2.在當前的格子和當前上方的格子擺一個骨牌.必須保證當前格子上方的那一個格子為0.

　　　　3.在當前的格子和當前左邊的格子擺一個骨牌,必須保證當前格子左邊的那一個格子為0,且當前格子上方的那一個格子不為0,否則會有空位.

　　　　然後初始化就是把第0個格子的(1<<m)-1設為1,因為你可以假設第0個格子的前m個格子都擺滿了骨牌.

　　　　由於n,m小於等於100,則n,m至少有一個小於等於10,把n,m中較小的一個賦給m就行了.

　　　　由於lrj書上的代碼用了滾動數組,所以我也用了.

　　　　還有,將i的第j為設為0,用位運算實現就是i&((1<<j)^-1),自己感受一下就知道了吧.

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=10
 
;
int n,m,cur; long long f[2][1<<maxn];
void clean(int d){
    for(int i=0;i<(1<<m);++i) f[d][i]=0;
}
int main(){
    for(;scanf("%d%d",&n,&m)!=EOF;){
        if(n<m) swap(n,m); clean(cur); f[cur][(1<<m)-1]=1;
        for(int i=1;i<=n;++i) for(int j=1;j<=m;++j){
            clean(cur
 
^=1);
            for(int k=0;k<(1<<m);++k){
                if((k>>(m-1)&1)) f[cur][(k<<1)&((1<<m)^-1)]+=f[cur^1][k];
                if(i!=1&&!(k>>(m-1)&1)) f[cur][(k<<1)^1]+=f[cur^1][k];
                if(j!=1&&!(k&1)&&(k>>(m-1)&1)) f[cur][((k<<1)&((1<<m)^-1))^3]+=f[cur^1][k];
            }
        }
        printf("%lld\n",f[cur][(1<<m)-1]);
    }
    return 0;
}

(輪廓線dp)UVA11270-Tiling Dominoes