題目描述

給出一棵樹，定義一個點到一條路徑的距離為這個點到這條路徑上所有點的距離的最小值。求一條長度不超過s的路徑，使得所有點到這條路徑的距離的最大值最小。

輸入

包含n行： 第1行，兩個正整數n和s，中間用一個空格隔開。其中n為樹網結點的個數，s為樹網的核的長度的上界。設結點編號依次為1, 2, ..., n。 從第2行到第n行，每行給出3個用空格隔開的正整數，依次表示每一條邊的兩個端點編號和長度。例如，“2 4 7”表示連接結點2與4的邊的長度為7。 所給的數據都是正確的，不必檢驗。

輸出

只有一個非負整數，為指定意義下的最小偏心距。

樣例輸入

5 2

樣例輸出

5

題解

樹的直徑+雙指針法+單調隊列

首先易證路徑一定在樹的直徑上（容易使用反證法證明）。

那麽可以找出樹的直徑，然後考慮答案是怎麽得到的：

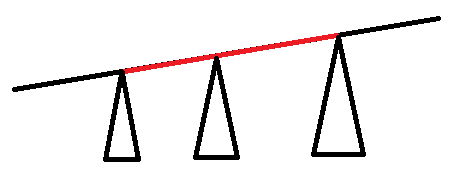
（上邊的直線是直徑，紅色的為選定路徑）

由於保證了是直徑，因此路徑左邊的貢獻只有直徑左端點到路徑左端點，路徑右邊的貢獻只有直徑右端點到路徑右端點；路徑中的貢獻為子樹（圖中三角形）中最遠的點。

那麽可以處理出每個點除直徑的子樹內最遠的點作為每個點的權值。

然後考慮：隨著左端點的移動，右端點的決策位置是單調不降的。因此可以使用雙指針法並用單調隊列維護區間最大值。

時間復雜度$O(n)$

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 500010
using namespace std;
int head[N] , to[N << 1] , len[N << 1] , next[N << 1] , cnt , fa[N] , deep[N] , vis[N] , v[N] , sum[N] , tot , q[N] , l , r;
inline void add(int x , int y , int z)
{
	to[++cnt] = y , len[cnt] = z , next[cnt] = head[x] , head[x] = cnt;
}
void dfs(int x)
{
	int i;
	for(i = head[x] ; i ; i = next[i])
		if(to[i] != fa[x])
			fa[to[i]] = x , deep[to[i]] = deep[x] + len[i] , dfs(to[i]);
}
void getdis(int x , int now , int p)
{
	int i;
	v[p] = max(v[p] , now);
	for(i = head[x] ; i ; i = next[i])
		if(!vis[to[i]])
			vis[to[i]] = 1 , getdis(to[i] , now + len[i] , p);
}
int main()
{
	int n , m , i , x , y , z , mx , p = 0 , ans = 1 << 30;
	scanf("%d%d" , &n , &m);
	for(i = 1 ; i < n ; i ++ ) scanf("%d%d%d" , &x , &y , &z) , add(x , y , z) , add(y , x , z);
	dfs(1) , mx = -1;
	for(i = 1 ; i <= n ; i ++ )
		if(deep[i] > mx)
			x = i , mx = deep[i];
	fa[x] = deep[x] = 0 , dfs(x) , mx = -1;
	for(i = 1 ; i <= n ; i ++ )
		if(deep[i] > mx)
			y = i , mx = deep[i];
	for(i = y ; i ; i = fa[i]) vis[i] = 1;
	for(i = y ; i ; i = fa[i]) getdis(i , 0 , ++tot) , sum[tot + 1] = sum[tot] + deep[i] - deep[fa[i]];
	for(i = 1 ; i <= tot ; i ++ )
	{
		while(p <= tot && sum[p + 1] - sum[i] <= m)
		{
			p ++ ;
			while(l <= r && v[q[r]] <= v[p]) r -- ;
			q[++r] = p;
		}
		ans = min(ans , max(max(sum[i] , sum[tot] - sum[p]) , v[q[l]]));
		if(q[l] <= i) l ++ ;
	}
	printf("%d\n" , ans);
	return 0;
}

【bzoj1999】[Noip2007]Core樹網的核 樹的直徑+雙指針法+單調隊列