微積分第一基本定理

　　如果F’(x) = f(x)，那麽：

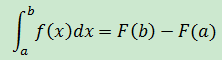
　　如果將F用不定積分表示，F =∫f(x)dx，微積分第一基本定理可以看作為是兩個不定積分賦予特定的值，再用符號連接起來，計算具體的數值。

　　這裏引入一個新符號：

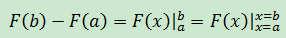
　　於是：

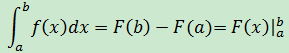
示例1

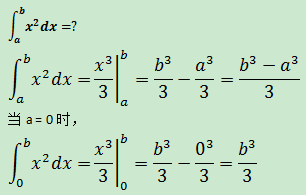
示例2

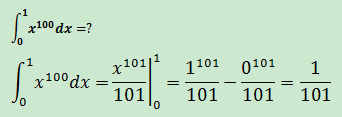
示例3

　　f(x) = sinx，求下圖陰影部分的面積

　　這實際上是積分的幾何意義。

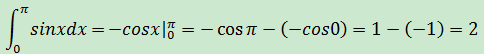
再看積分的幾何意義

　　如果s = S(t)是距離關於時間的函數，那瞬時速度就是S’(t) = ds/dt = V(t)，從時間a到時間b所經過的距離是：

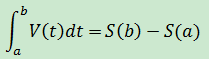
　　dt = 1秒，用黎曼和表示：

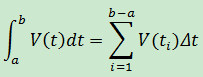
　　V(t)就是汽車儀表盤上的速度，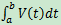

　　如果行駛一段時間後掉頭，再回到出發點，按照黎曼和表示法將會出現相反的速度，最後的結果是0。這樣看來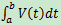， 表示的就是位移而不是行駛裏程，其裏程應當是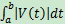

　　再來看一個例子，曲線是sinx，0 ≤ x ≤ 2π，求曲線和x軸間兩個駝峰的面積。

　　這肯定不對了，原因是上篇文章提到的概念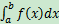：“ 是y=0,x=a,x=b,y=f(X)所圍成圖形的面積”並不完全正確。當曲線在x軸上方是，定積分才是面積；在下方是，面積（積分值）是負的。之前的幾何解釋是不完全的，它掩蓋了某些事實，關於定積分真正的幾何解釋是：定積分是x軸上方的面積減去x軸下方的面積。

定積分的性質

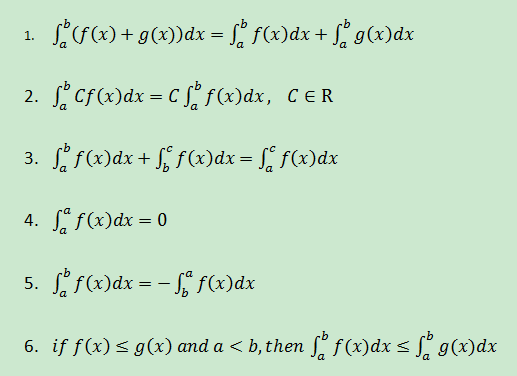
定積分的換元法

　　變量替換是定積分的另一個性質，這個性質結合了不定積分的換元法（關於換元法的描述：數學筆記11——微分和不定積分）。定積分換元法性質：

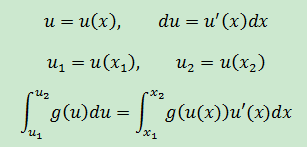
　　這個性質僅在u’在積分限上不變號時才有效，即u’(x)和u(x)在[x₁, x₂]上必須同號。

示例1

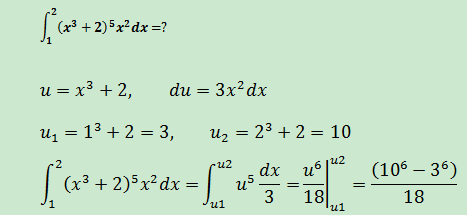
示例2

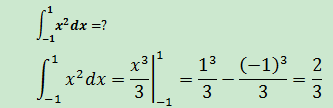
　　這是正確答案。如果使用換元法：

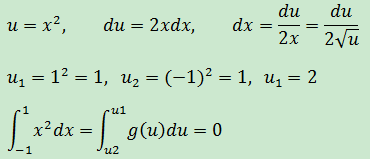
　　答案是錯誤的，其違反了定積分換元法的約束條件，u = x², u’ = 2x，當x = -1時，u’ = -2，當x = 1時， u‘ = 2, u’不同號。對於此例，du = 2xdx實際上應該是 dx =± u^-1/2du/2

綜合示例

示例1

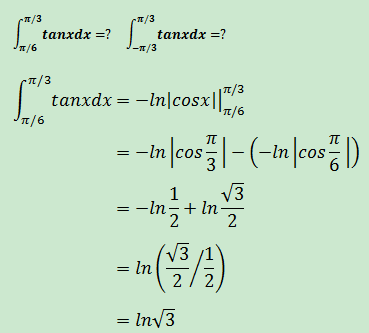
　　第二個式子也可以用上述方法計算，但是可以使用更簡單的方法直接得到答案。

　　如上圖所示，tanx 在[-π/3, π/3]上是關於原點對稱的，根據定積分的幾何意義，x軸上方的面積減去x軸下方的面積，故可以直接得出答案0。

　　註：

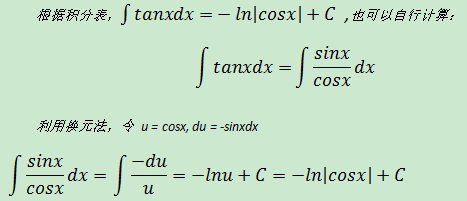
示例2

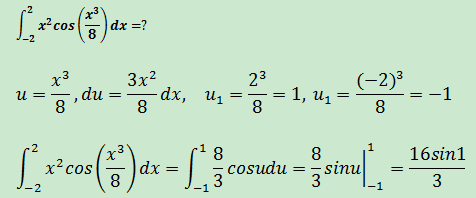
總結

　　1.定積分第一基本定理：如果F’(x) = f(x)，那麽：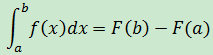

　　2.定積分的幾何意義是x軸上方的面積減去x軸下方的面積。

　　3.定積分的性質：

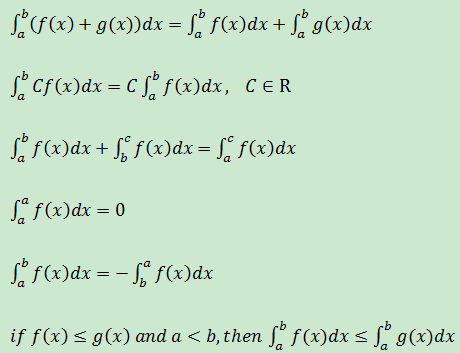　　4.定積分換元法

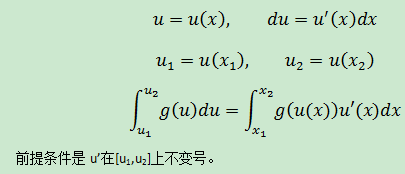
　　作者：我是8位的

　　出處：http://www.cnblogs.com/bigmonkey

　　本文以學習、研究和分享為主，如需轉載，請聯系本人，標明作者和出處，非商業用途！

數學筆記14——微積分第一基本定理