一、第一中值定理

如果函式f(x)在閉區間[a，b]上連續，則在積分割槽間[a，b]上至少存在一個點$\xi $，使得$\int_{a}^{b}f(x)dx=f(\xi )(b-a).(a\leqslant \xi \leqslant b)$

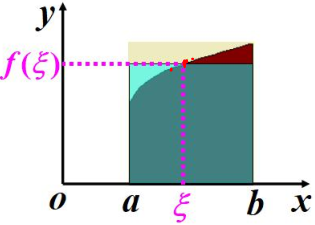
二、微積分基本定理

積分上限函式：函式f(x)在區間[a，b]上連續，對於定積分$\int_{a}^{x}f(x)dx$每一個取值的x都有一個對應的定積分值。記作：$\Phi (x)=\int_{a}^{x}f(t)dt$

定理1：

定理2（原函式存在定理）：

三、牛頓—萊布尼茲公式

牛頓-萊布尼茲公式（Newton-Leibniz formula），通常也被稱為微積分基本公式，它揭示了定積分與被積函式的原函式或者不定積分之間的聯絡。

如果F(x)是連續函式f(x)在區間[a，b]上的一個原函式，則：$\int_{a}^{b}f(x)dx=F(b)-F(a)$

解釋：一個連續函式在區間[a，b]上的定積分等於它的任意一個原函式在區間[a，b]上的增量

幾何解釋：

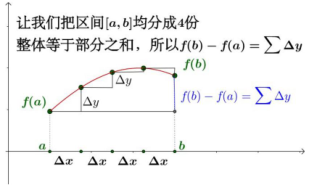
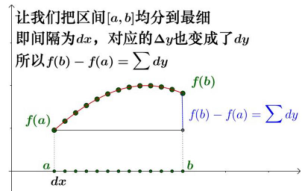
可得：$f(b)-f(a)=\sum dy$，由於$dy={f}'(x)dx$，所以 $f(b)-f(a)=\sum f'(x)dx=\int_{a}^{b}f'(x)dx$

例題：求解$\int_{0}^{\frac{\pi }{2}}(2\cos x+\sin x-1)dx$

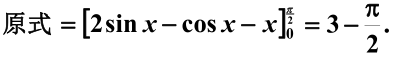
定理3（微積分基本公式）：

有$f(x)\in C[a,b]$，且$F'(x)=f(x)$

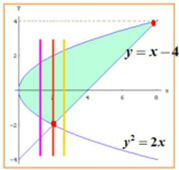
例題：計算由曲線y²=2x和直線y=x-4所圍成的圖形的面積

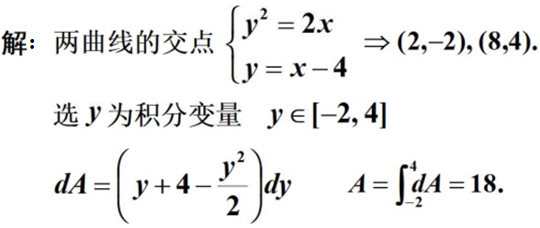
四、泰勒公式

簡單來講就是用一個多項式函式去無限逼近一個給定的函式(即儘量使多項式函式影象擬合給定的函式影象，如sin x，cos x等函式值的近似計算)，注意，逼近的時候一定是從函式影象上的某個點展開。如果一個非常複雜函式，想求其某點的值，直接求無法實現，這時候可以使用泰勒公式去近似的求該值，這是泰勒公式的應用之一。泰勒公式在機器學習中主要應用於梯度迭代。

首先回憶微分 

若$f'(x_{0})$存在，在$x_{0}$附近有$f(x_{0}+\Delta x)-f(x_{0})\approx f'(x_{0})\Delta x$。

由於$\Delta x=x-x_{0}$，可以得到$f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})$，

近似可得$f(x)\approx f(x_{0})+f'(x_{0})(x-x_{0})$。

接著再來引出泰勒公式，如果說我們想要以直線來近似的代替一個曲線，如下圖所示

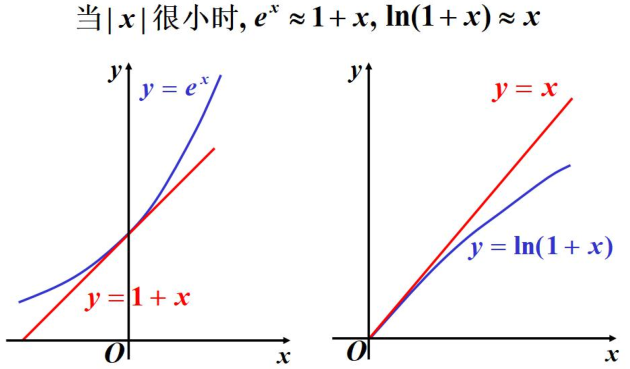
只用一階導數看起來有點不準呀，如上圖所示，能不能在利用一些呢？答案肯定是可以的，一階導數只幫我們定位了下一個點是上升還是下降，然後對之後的趨勢就很難把控了。

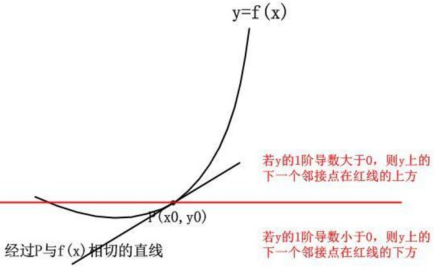
那如何定位的更準確一些呢？如果我們再把二階導數利用上呢？

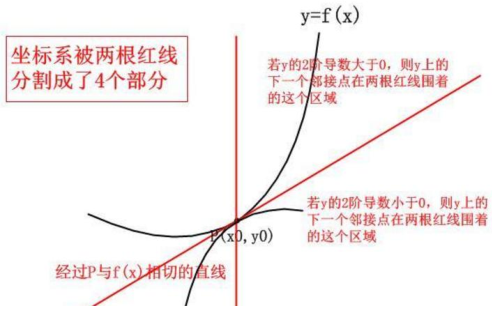
我們可以發現，這樣的方式存在精確度不夠高，誤差不能估計等不足之處。所以，主要的問題就是尋找函式P(x)，使得f(x)≈P(x)，從而使得誤差R(x)=f(x)-P(x)可估計。

分析：如果說要f(x)≈P(x)，且近似程度要好，P_n(x)應該滿足什麼條件？

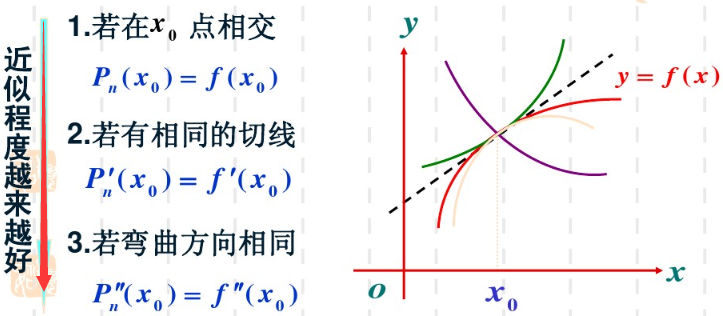
由上圖就可以引出泰勒公式了

$P_{n}(x)=f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+\cdots +\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}$稱為f(x)在點x₀關於(x-x₀)的n階泰勒多項式，這個式子只能說是得到的值能夠無限的逼近真正的函式值，但是其中還存在一個誤差項R(x)，也就是說f(x)=R(x)+P(x)，這裡的誤差項稱為餘項。對於一般的機器學習、深度學習來說，餘項本身也用不上在加上其比較複雜，所以在這裡就不作解釋了。

五、泰勒公式詳細解釋

多項式逼近如下圖所示

公式裡面的階數是什麼意思呢？

階數越高增長速度越快。觀察可發現，越高次項在越偏右側影響越大。對於一個複雜函式，給我們的感覺是在當前點，低階項能更好的描述當前點附近，對於之後的走勢就越來越依靠高階的了。

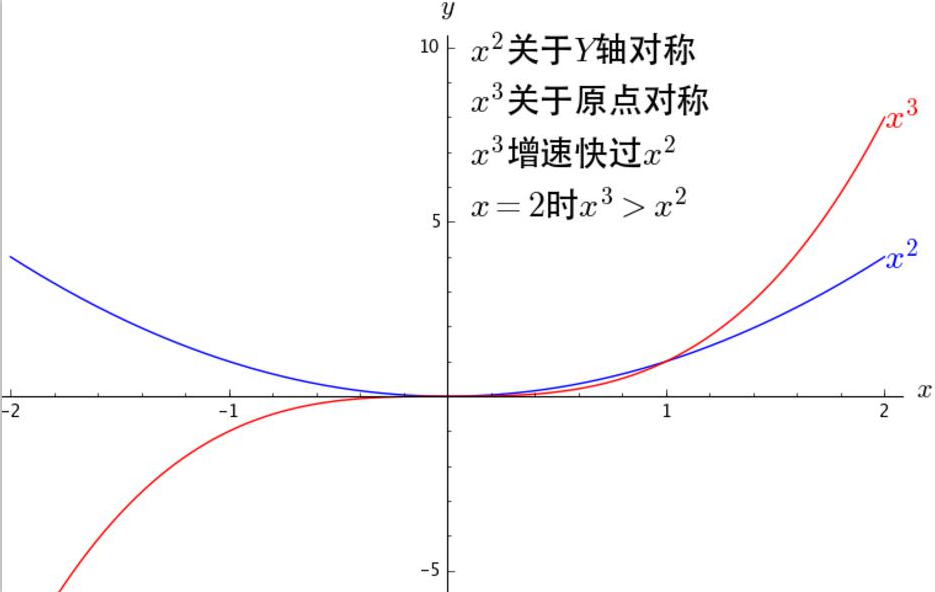
公式裡面的階乘是什麼意思呢？

如果把9次的和2次的直接放在一起，那2次的就直接不用玩了呀，它們之間的差距太大了。但是在開始的時候應該是2次的效果更好，之後才是慢慢輪到9次的。

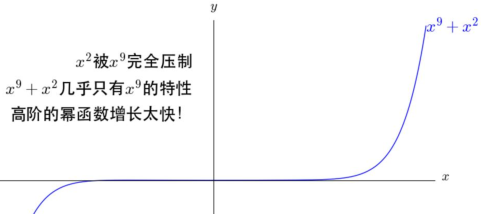
 有了階乘(!)之後，就幫助我們解決了這樣的問題

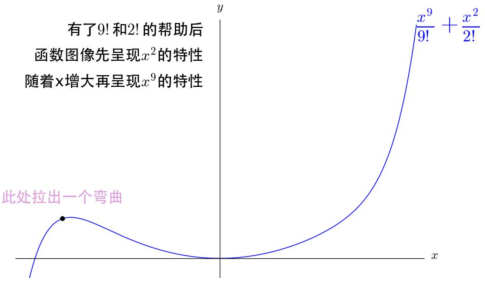
如下圖所示，使用不同階的多項式函式來逼近$y=\sin x$函式

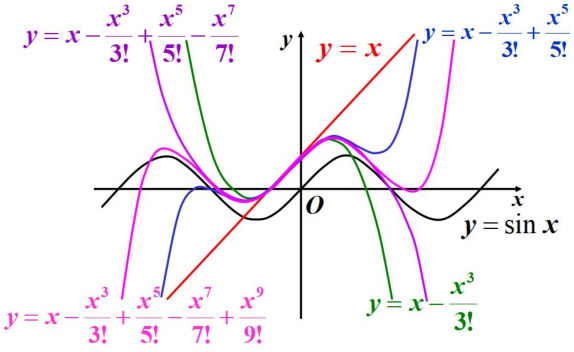
可以看到，階數越高的函式越能擬合$y=\sin x$函式