關於機器學習中數據降維的相關方法
前言
在之前一些文章的討論中，通過一些例子我們可以發現（主要是關於決策樹或隨機森林的相關內容）其實並不是樣本的所有屬性可能都是那麽得重要，只要不是同等重要，特別是在分類問題上可能可以去除一些屬性或特征（一般決策樹需要進行剪枝，其實剪枝的原因就在於此）依然能夠得到較好的結果（盡管在一些場合會損失掉準確性），那麽這個問題的實質其實就是機器學習的降維問題。
對於數據進行降維的處理，不僅可以使得在計算上可能更為簡便或簡單，而且可以更為節省存儲資源，如計算機的硬盤或內存等。數據對象能夠被降維，那麽它的一些可以被去除的特征就一定不是太重要，或者說某些特征和另外一些特征存在一定程度的關聯，而且關聯的程度越深則去除這些特征所導致的結果就和原來問題之間的差別越小。
本文所涉及的降維方法其實也是比較主流的幾種，包括主成分分析（Principal ComponentsAnalysis，簡稱PCA）、奇異值分解（Singular Value Decomposition，簡稱SVD）、局部線性嵌入（Locally Linear Embedding，簡稱LLE）以及多維度尺度分析等，還會涉及到關於多分類情況下的降維方法——Fisher方法，最後還會要簡單地討論下關於降維問題的逆問題，主要是字典學習和稀疏表示，在討論這個方法時，還會涉及到SVD方法，只不過是被稱作KSVD而已。
個人以為數據的降維方法不能完全歸類於機器學習範疇（因為機器學習的本質不完全是優化指令，而是從數據中獲取經驗，從而提升輸出效用），但數據降維的好處是在於可以減少運算量。
主成分分析及奇異值分解
在闡述比較通用的奇異值分解問題之前，本文先討論下關於主成分分析的相關內容。對於主成分分析的定義是（利用數學語言）：一個正交化線性變換，把數據變換到一個新的坐標系統中，使得這一數據的任何投影的第一大方差在第一個坐標（稱為第一主成分）上，第二大方差在第二個坐標（第二主成分）上，依次類推。
從上述定義所涉及的相關內容上看，主成分分析（有的地方被稱為主元分析）根本上就是找到一組正交向量把在高維坐標系下的點相應地變換到低維坐標系上，其變換依據其實就是特征值及其特征向量，在變換的過程中會舍棄一些特征值及其特征向量，而被舍棄的這些東西是對最終變換所形成的結果沒有特別大的影響（因為就其表現而言，相關方差較小），所以這種方法才被成為主成分
在較為形式化地闡述這個問題之前，先對一些符號的使用進行約束。本文默認的認為具有較高維度數據或對象的維度為p，而具有較低維度的數據或對象的維度是d（網上絕大多數文章使用的分別是m和r），而對象的數量（樣本的數量）依舊是N。
對於正交化的向量（也被稱作正交化的基）定義（因為我們討論的是降維情形，故假設有p個）如下：
而我們還引入x0作為原坐標的原點，在後面的推導過程中可以看出這個原點其實就是原樣本的均值。
對於相關變換，我們希望其盡量不存在差異或者差異越小越好，故有如下目標函數：
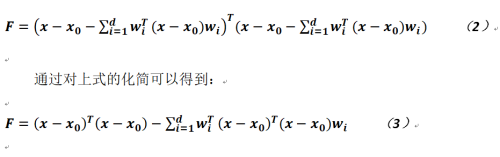
如果上式的結果為零，就可以認為降維的任務被完美地完成，但這幾乎是不可能的事情，故只要足夠小就可以了，所以我們在上式的基礎上加入約束，利用拉格朗日乘數法能夠對如下函數計算相關參數的取值（對於所有樣本點）：
由公式6可以看出
就是相關特征值，而且由於上式的左半部分是一個半正定矩陣，故其特征值一定是大於等於0的，所以我們能夠得到一個化簡後的函數：
至此我們就得到了一個主成分分析在數學上的解釋。需要註意的是，為了使得公式8最小，則需要將這些特征值由大至小地進行排列方能獲得正確的結果。
以上的推導過程可能與網上的相關文章介紹多少有些區別，因為大多數文章的描述主要是針對樣本的協方差進行的，這個其實和本文沒有太大的不同，只不過角度上略有差異。而且本文所使用的方法和SVD算法幾乎是一樣的，所以以下只簡單的再描述下主流方法的相關內容。
關於主成分分析，一般的過程如下：
對於樣本矩陣X，求解其協方差矩陣Σ；
對於協方差矩陣Σ,求解其特征值
（共p個）；對於這些特征值計算特征向量ξi，根據降維的需要及其大小排列組成變換矩陣Q（保留d個特征值最大的特征向量）；
利用變換陣Q，計算降維的樣本矩陣Y中每一個樣本
：。
從上面的求解步驟可以看出，這個和之前的推導沒有區別，只不過之前的方法可能在原理上更為清晰和明確，因為它體現了在機器學習理論中對於一致性（錯誤越少越好）和緊致性（類內差異越小越好）的要求，而其它的一般性的對於主成分分析法並沒有在原理上講述的那麽清楚（一般沒有交代為什麽需要在p個協方差中獲取值最大的d個方差）。
順便說一下，其實很多工具都提供了計算相關工具，比如說計算矩陣的特征值、特征向量，如在R中，就可以使用函數eigen來計算。
在討論完主成分分析後，我們在來看下關於奇異值分解問題（其實這個問題在討論完主成分分析後再進行論述的意義不是太大，或者我們可以先討論SVD再講述PCA，但考慮到完整性，這裏還是再次簡要的闡述其方法）。
奇異值分解就是基於如下的一個公式：
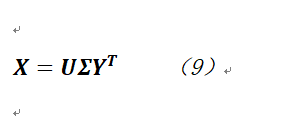
為了與前面保持一致，其中X是樣本矩陣，其維度是p，共有N列（樣本的數量），而U則是一個p*p的正交方陣，其向量被稱作左奇異向量；而Σ是一個p*N的矩陣，其對角線上為奇異值（這些奇異值應被從大到小進行排列），其它元素為0；最後Y則是以一個N*N的正交方陣，其向量被稱作右奇異向量。
那麽有了上述公式，改如何降維？我們可以將公式9改成一個對近似公式的求解：
數據降維的結構性保證
在對數據降維後，如何保證降維後的在結構上一些不變特性，從而達到數據不至於被過多地扭曲或變形，本節主要就是從局部和全局角度來討論這個問題。
局部線性嵌入
局部線性嵌入的目標就是在數據降維後仍然保留原始的高維數據的拓撲結構，這種拓撲結構主要表現在數據點局部的鄰接關系上。
而描述這種鄰接關系，主要是利用數據點局部的鄰接點之間的線性組合，即我們希望最小化如下的目標函數：
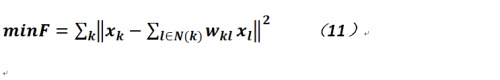
其中N(k)是樣本點的鄰接樣本點，而是連接權值，它們的和等於1。那麽對於公式11的在約束下的求解就能夠得到相關參數的解。
以下令為的K個近鄰所構成的矩陣，而令，為向量系數，則公式11可以改寫為如下形式：
那麽利用上述被求出的相關連接參數，當數據點嵌入到低維空間時，有如下目標函數：
註意公式18所求取的目標函數是一個Frobenius範數，這個範數又被稱作F範數，它和矩陣的1範數、2範數、p範數以及無窮範數均不相同，讀者可以參看相關文檔。
通過對上式求解，我們可以得到相關結論為：
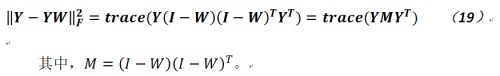
通過推導，可以看出如若想公式19的值盡量得小，則應取矩陣M的最小d個特征值，但其最小值一般非常接近於0，則應取2到d+1個特征值及其對應的特征向量。
不過局部線性嵌入的應用存在一定局限性，主要是將其用於開放式的流型處理，而且對於k緊鄰的選擇需要註意，不能過小也不宜過大（一般認為至少不能超過降維後的維度大小）。目前有多種對於這個算法的改進，主要在於對於鄰接點的選擇，最好是在以嵌入點為中心的超球體的周邊均勻地尋找鄰居樣本（可利用余弦夾角），則這樣的效果更好。
多維度尺度分析及等距映射
上節的局部線性嵌入著重從局部出發，保證降維後的數據仍然保留原始數據的局部鄰接特征，而多維度尺度分析及等距映射乃是從全局角度出發對數據進行降維，也就是說降維後的數據仍能保持在高維坐標下的任意兩點間距離關系。
現令數據在高維下的距離為DX，而數據在低維下的數據為DY，那我們的目標函數就是：
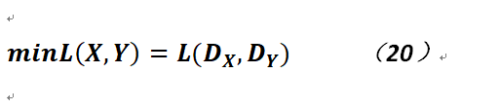
也就是說降維之前的距離和降維之後的距離差異盡量得小，上式也可以寫成如下形式：
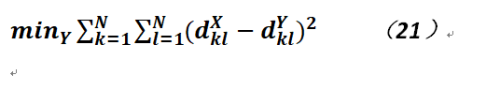
其中，和分別是降維之前點k、l之間的距離以及降維之後兩點之間的距離。這兩點之間的距離可以采用歐式距離。
現定義矩陣T，它是N*N方陣，且矩陣的元素：
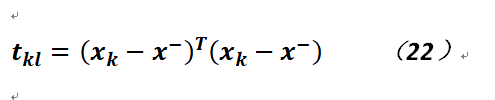
是樣本均值向量，然後展開上式，最終可以得到如下公式：
求解上述問題只要對矩陣T進行特征分解即可，如把數據降到d維，則只需提取前d個特征向量。
多分類數據降維
不知讀者是否註意，本文之前的相關降維討論，除了對於特征及特征向量求取，其實也大都會涉及到均值的計算或使用，而之前我們只是默認這些待降維的樣本都是來自同一類別，而本節會討論下多分類的降維問題。
在推導多分類降維公式前，根據由簡到難的研究思路，首先研究下二分類的數據降維。
以下就是根據Fisher線性判別式進行討論的。
設若樣本集合為，其中是樣本的類標，在二分類的情況下就是1和0，每個樣本表示為p維特征向量。Fisher線性判別分析將N個樣本投影到低維空間而得到。
而分類線性判別分析希望找到一個由d維向量w定義的投影方向，將樣本x投影到向量w上，從而樣本維度由p維降到1維，而在降維後樣本的可分性更好。
假設v1和v2分別是樣本X兩個分類的均值，則我們希望這兩個類中的樣本和其均值具有最小的差異。以下給出兩個類的類內差異：
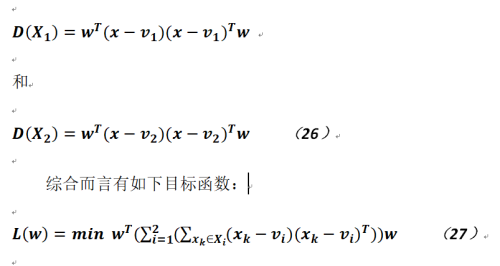
對於公式27而言，在二分類情況下i的取值範圍只是1和2。
根據上式定義類內散布差異矩陣：
通過對於公式28的求解即可得v1和v2分別就是類1和類2的樣本均值。
既然有了類內差異評估公式，很自然的也有類間差異評估，而我們要求這個類間差異越大越好：
在分析了二分類線性判別之後，關於多分類線性判別相關內容就呼之欲出了，其公式與而分類在形式上幾乎沒有太大差別，只不過在分析類間差異時使用了樣本總體均值v。
對於c個類的類內差異定義如下：
在公式33中，v就是樣本總體的均值。
故通過上述推導，可知只要最大化如下函數即可：
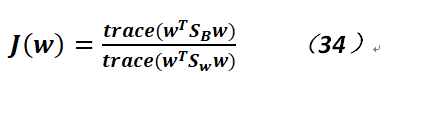
字典學習和稀疏表示
有時我們需要考慮對於稠密的樣本點時，如何在更高維獲取其相對稀疏的表示（這樣做的目的是什麽？），而進行這類變換的矩陣中的向量就被稱作字典。更為形式化的表達就是，對於在維度為d的空間中的若幹樣本組成的矩陣Y，需要尋找字典矩陣W=[w1,w2,...,wp]進行相應地轉換（字典中的向量是d維的，共p個向量），轉換後的相對稀疏的矩陣輸出為X，這個輸出矩陣的維度為p，而且p > d，整個過程被稱作字典學習。
綜上所述，對於結果，我們希望最小化如下目標函數：
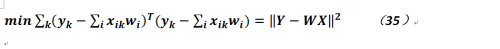
但是能滿足上式的坐標系過多，我們應該選擇一個最為簡單的形式，即在高維空間中向量所含0的個數越多越好（當然不一定是全0，否則沒有任何意義；這裏就看出對於稀疏的要求），而這個要求恰是矩陣的0範數，但由於0範數沒有相關的解析式，也無法直接求解，故我們轉而求其次使用1範數，所以公式35被寫作如下形式：
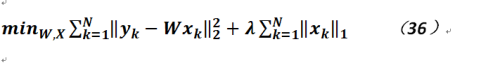
在公式36中，可以看出需要最小的參數實際上包含了字典和Y在高維空間稀疏的表示形式X。而如何求解此公式中的？因為其中包含了1範數，故公式不可導，只能使用和LASSO回歸類似的方式求解（即FIST方法）。
對於如何求解公式36中的字典？這裏需要使用所謂的KSVD方法，如下：
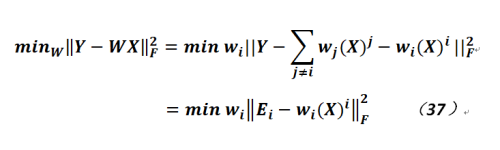
是X的第i行（不是i列，否則就是一個樣本了），而是字典向量。那麽，該如何理解上式？實際上就是評估待求字典的第i列對於輸出的相關影響。
KSVD的運作過程如下：
將矩陣Ei進行SVD分解；
使用分解後的第一個左奇異向量（列向量）更新字典
；使用分解後的第一個右奇異向量（列向量）乘以第一個特征值更新
；選取下一個進行分解。
這樣交叉更新和字典，直至整體收斂為止。
註意在更新字典和時，應只更新對應的非0元素（故其實對於也應進行收縮，即刪去元素為0的部分，重新組織成一個新的矩陣），否則無法保證矩陣X的稀疏性質。對於這個算法而言，筆者的理解就是評估最為顯著部分對於升維的影響，因為對於矩陣進行SVD分解後，其第一個特征值是最大的（相應的，其特征向量也是最為顯著或可以說其顯著水平最高）。
關於機器學習中數據降維的相關方法