洛谷P3941入陣曲

【題目描述】

　　丹青千秋釀，一醉解愁腸。 無悔少年枉，只願壯誌狂。

小 F 很喜歡數學，但是到了高中以後數學總是考不好。 有一天，他在數學課上發起了呆；他想起了過去的一年。一年前，當他初識算法競賽的 時候，覺得整個世界都煥然一新。這世界上怎麽會有這麽多奇妙的東西？曾經自己覺得難以 解決的問題，被一個又一個算法輕松解決。 小 F 當時暗自覺得，與自己的幼稚相比起來，還有好多要學習的呢。 一年過去了，想想都還有點恍惚。 他至今還能記得，某天晚上聽著入陣曲，激動地睡不著覺，寫題寫到雞鳴時分都興奮不 已。也許，這就是熱血吧。

也就是在那個時候，小 F 學會了矩陣乘法。讓兩個矩陣乘幾次就能算出斐波那契數列的 第 10^100 項，真是奇妙無比呢。 不過，小 F 現在可不想手算矩陣乘法——他覺得好麻煩。取而代之的，是一個簡單的小 問題。他寫寫畫畫，畫出了一個 ?? × ?? 的矩陣，每個格子裏都有一個不超過 ?? 的正整數。 小 F 想問問你，這個矩陣裏有多少個不同的子矩形中的數字之和是 ?? 的倍數？ 如果把一個子矩形用它的左上角和右下角描述為 (??1,??1,??2,??2)，其中??1 ≤ ??2,??1 ≤ ??2； 那麽，我們認為兩個子矩形是不同的，當且僅當他們以 (??1,??1,??2,??2) 表示時不同；也就是 說，只要兩個矩形以 (??1,??1,??2,??2) 表示時相同，就認為這兩個矩形是同一個矩形，你應該 在你的答案裏只算一次。

【輸入格式】

　　 從文件 rally.in 中讀入數據。 輸入第一行，包含三個正整數 ??,??,??。 輸入接下來 ?? 行，每行包含 ?? 個正整數，第 ?? 行第 ?? 列表示矩陣中第 ?? 行第 ?? 列 中所填的正整數 ????,??。

【輸出格式】

　　輸出到文件 rally.out 中。 輸入一行一個非負整數，表示你的答案。

【樣例 1 輸入】

　　2 3 2

　　1 2 1

　　2 1 2

【樣例 1 輸出】

　　 6
【樣例 1 說明】

　　 這些矩形是符合要求的： (1, 1, 1, 3)，(1, 1, 2, 2)，(1, 2, 1, 2)，(1, 2, 2, 3)，(2, 1, 2, 1)，(2, 3, 2, 3)。

【樣例 2】

　　 見選手目錄下的 rally/rally2.in 與 rally/rally2.ans 。


【數據範圍與約定】

　　子任務會給出部分測試數據的特點。如果你在解決題目中遇到了困難，可以嘗試只解 決一部分測試數據。 每個測試點的數據規模及特點如下表：

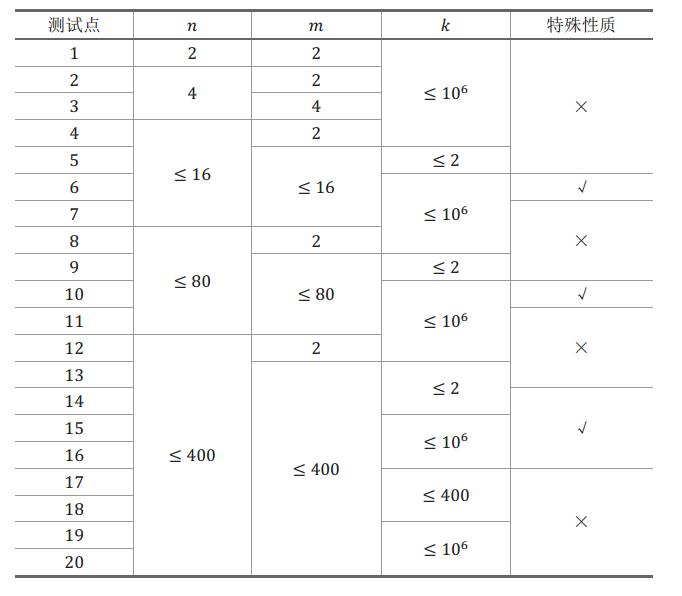
特殊性質：保證所有 ????,?? 均相同。

看到這道題，我想到了前幾天做的牛宮，給定寬的上下界，再枚舉長，看該矩陣和是否為k的倍數（當然不可能暴枚舉），

易發現，若有兩個矩陣和除以k的余數相同，那麽這兩個矩陣和相減必定為k的倍數。

也就是說，只要子矩陣模k下的余數出現兩次，那麽該矩陣必定包含一個為k的倍數的矩陣。

所以處理出前綴和模k，統計情況即可。

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 using namespace std;
 5 int n,m,mod;
 6 long long a[401][401];
 7 int s[4010][4010],f[2222222],sum[2222222];
 8 long long ans;
 9 int main()
10 {
11    scanf("%d%d%d",&n,&m,&mod);
12    for(int i=1;i<=n;i++)
13    for(int j=1;j<=m;j++)
14    {
15      scanf("%lld",&a[i][j]);
16      s[i][j]=(s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j])%mod;
17    }
18    for(int i=0;i<n;++i)
19    for(int j=i+1;j<=n;++j)
20    {
21      f[0]=1;
22      for(int k=1;k<=m;++k)
23      {
24          sum[k]=((s[j][k]-s[i][k])%mod+mod)%mod;//防止出現負數 
25          ans+=f[sum[k]]; 
26          f[sum[k]]++; 
27      }
28      for(int k=1;k<=m;++k)
29      f[sum[k]]=0;
30    }
31   cout<<ans<<endl;
32   return 0;
33 }

洛谷P3941入陣曲