四中矩陣相乘方法對比
阿新 • • 發佈:2017-11-04
mage idt -128 img ear char ras 隨機 元素
在公茂果老師的課件中,給出了三種矩陣相乘的方法:
1. 利用矩陣定義,對矩陣進行運算。即C(i,j)=A(i,k)*B(k,j),時間復雜度為:
- 每一個元素需時間n
- C矩陣共有n2個元素
- 因此,總的時間復雜度為n3
其實現代碼為:
tic;
C2=zeros(n(m));
for i=1:n(m)
for j=1:n(m)
for k=1:n(m)
C2(i,j)=C2(i,j)+A(i,k)*B(k,j);
end
end
end
t2(m)=toc;
2.利用分治法進行計算。分治法的核心,在於將原問題切割,這裏將原矩陣A與B,分別切割成四個子矩陣,分別得到C11,C12,C21,C22,在矩陣相乘階段,利用的是MATLAB自帶的矩陣相乘函數。
對於C11為例,其時間復雜度為:
- 每一個元素需要時間為n/2
- 共有(n/2)2個這樣的元素
- 因此,其時間復雜度為(n/2)3
- 總時間為上一個的1/8
期實代碼為
A11=A(1:n(m)/2,1:n(m)/2);
A12=A(1:n(m)/2,n(m)/2+1:n(m));
A21=A(n(m)/2+1:n(m),1:n(m)/2);
A22=A(n(m)/2+1:n(m),n(m)/2+1:n(m));
B11=B(1:n(m)/2,1:n(m)/2);
B12=B(1:n(m)/2,n(m)/2+1:n(m));
B21=B(n(m)/2+1:n(m),1:n(m)/2);
B22=B(n(m)/2+1:n(m),n(m)/2+1:n(m));
%矩陣計算,開始計時
tic;
C3=zeros(n(m));
C11=A11*B11+A12*B21;
C12=A11*B12+A12*B22;
C21=A21*B11+A22*B21;
C22=A21*B12+A22*B22;
C3=[C11 C12;C21 C22];
t3(m)=toc;
3.利用Strassen方法

上面的圖片,已經給的非常的清楚,其時間復雜度為n2.81
下面貼出完整的代碼
clc;
close all;
clear all;
n=[2^2 2^3 2^4 2^5 2^6 2^7 2^8 2^9 2^10 2^11 2^12];
for m=1:11
%%%%采用MATLAB自帶函數進行矩陣相乘
A=round(rand(n(m)));%生成隨機矩陣A
B=round(rand(n(m)));%生成隨機矩陣B
%自帶函數計時
tic;
C1=A*B;
t1(m)=toc;
%按照矩陣相乘的定義進行計算
tic;
C2=zeros(n(m));
for i=1:n(m)
for j=1:n(m)
for k=1:n(m)
C2(i,j)=C2(i,j)+A(i,k)*B(k,j);
end
end
end
t2(m)=toc;
%分治法,思路,對AB矩陣進行切割後,仍使用MATLAB自帶的函數進行
%步驟一,將原來的矩陣分塊切割成四個,這四個子矩陣,還會用到Strassen的方法中
A11=A(1:n(m)/2,1:n(m)/2);
A12=A(1:n(m)/2,n(m)/2+1:n(m));
A21=A(n(m)/2+1:n(m),1:n(m)/2);
A22=A(n(m)/2+1:n(m),n(m)/2+1:n(m));
B11=B(1:n(m)/2,1:n(m)/2);
B12=B(1:n(m)/2,n(m)/2+1:n(m));
B21=B(n(m)/2+1:n(m),1:n(m)/2);
B22=B(n(m)/2+1:n(m),n(m)/2+1:n(m));
%矩陣計算,開始計時
tic;
C3=zeros(n(m));
C11=A11*B11+A12*B21;
C12=A11*B12+A12*B22;
C21=A21*B11+A22*B21;
C22=A21*B12+A22*B22;
C3=[C11 C12;C21 C22];
t3(m)=toc;
%Strassen方法,公茂果老師的課件中,已經給出了初始化方法
tic;
C4=zeros(n(m));
M1=A11*(B12-B22);
M2=(A11+A12)*B22;
M3=(A21+A22)*B11;
M4=A22*(B21-B11);
M5=(A11+A22)*(B11+B22);
M6=(A12-A22)*(B21+B22);
M7=(A11-A21)*(B11+B12);
C11=M5+M4-M2+M6;
C12=M1+M2;
C21=M3+M4;
C22=M5+M1-M3-M7;
C4=[C11 C12;C21 C22];
t4(m)=toc;
end
%這裏四個方法已經全部結束,接下來就是輸出圖片
x=log(n)/log(2)%橫軸取對數
plot(x,t1,x,t2,x,t3,x,t4);
xlabel(‘log(n)/log(2)‘);
ylabel(‘time‘);
title(‘The comparison chart of four different methods for Matrix multiplication‘)
運行時間比較長,請耐心等待。其結果為:
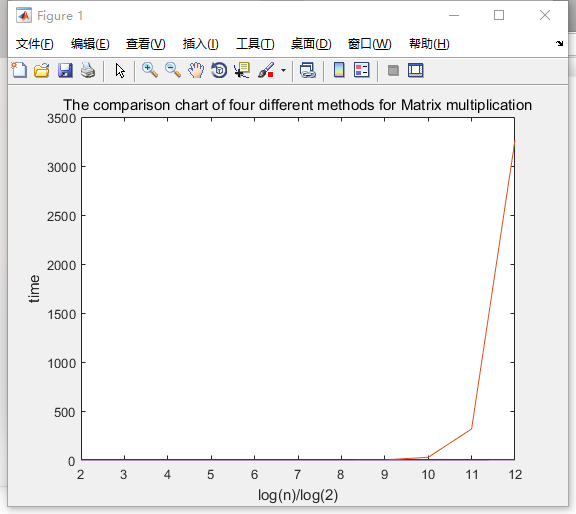
沒設置好,所以,看著不是特別清楚,可以在關鍵的節點處,設置*等,特別現實一下。
四中矩陣相乘方法對比
