定積分除了計算面積外，還可以應用在計算體積上。

圓盤法

　　一條曲線y = f(x)，如果曲線繞x軸旋轉，則曲線經過的區域將形成一個橄欖球形狀的體積，如下圖所示：

曲線繞x軸旋轉一周

　　現在要計算體積。我們依然按照黎曼和切片的思路去計算，只不過這回需要一點想象力。

　　將上圖的矩形繞x軸旋轉一周將得到一個半徑為y，高度為dx的圓盤：

矩形框繞x軸旋轉一周

　　該圓盤的面積S(x)≈π(f(x))²，體積： Δv ≈ S(x)Δx，如果將整個圖形的體積切成n個圓盤：

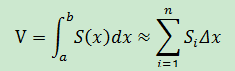
　　這就是圓盤法。

示例

　　求半徑為a的球的體積。

　　通過球體的公式可知，V =πa³(4/3)，假設我們不知道這個公式，使用圓盤法求解。

　　先將球體的最大橫截面投影到直角坐標系上，在對圓的上半部分切割，旋轉，如下圖所示：

　　圓盤的底面積≈πy²dx，由此可以得到球體體積：

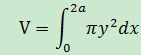
　　還需要將y轉換為x。根據上圖中圓的公式(x – a)² + y² = a²，可得出y² = 2ax - x²，於是：

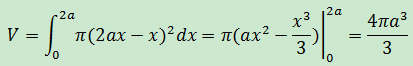
　　實際上我們得到了更多的信息，如果僅計算部分球體的體積，依然可以使用上面的結論，僅改變積分上限即可，如下圖所示：

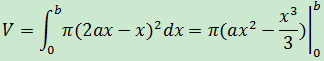
　　實際上可以把V = π(ax² – x³/3)看作球體切片的公式。

殼層法

　　假設坩堝內壁的橫截面曲線是y = x²，深度是a，計算坩堝的容積。

計算坩堝的容積

　　我們依舊可以使用圓盤法計算，這是這次是繞y軸旋轉：

圓盤法

　　圓盤的高度是Δy，所以需要將原函數轉換成y關於x的函數，在正半軸上，x = y^1/2

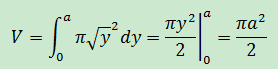
　　對於本例來說，圓盤法沒有問題，如果曲線的公式再復雜一點，就需要在反函數的轉換上耗費時間，如果我們直接縱向切割，使用dx代替dy，就無需對原函數進行轉換：

　　矩形繞y軸旋轉一周將得到一個圓環，其厚度是dx，半徑是x，高度是a – x²，如下圖所示：

　　如果展開圓環，將得到一個底面積是圓環周長，高度是dx的長方體，其體積：

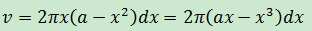
　　由此，坩堝的容積是：

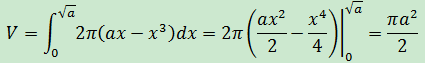
單位產生的悖論

　　在計算坩堝的容積時，我們最終得到V = πa²/2，如果坩堝深度是1m，代入公式得到π/2（m³）；現在將1m換成100cm，因為高度是一樣的，所以我們期待得到同樣的結果，但是代入公式後，最終得到10000π/2（cm³

　　問題出在哪呢？仔細觀察最終結果的積分形式：

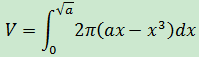
　　積分的上限是a^1/2，1^1/2 = 1，100^1/2 = 10，因此單位不同將得到不同的結果。實際上這個公式違背了比例原則，將所有問題數學化的同時並沒有考慮到物理學中的量綱。這就好比重力加速度是9.8，但這個9.8是有單位的，單位是米每二次方秒，如果長度單位采用厘米，這個常數9.8也需要相應變化才能適用。

示例

示例1

　　求y = 5和y=x² + 1所圍圖形繞y軸旋轉後得到的體積。

　　用圓盤法計算，圓盤繞y軸旋轉，如下圖所示：

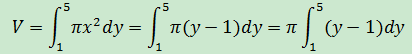
示例2

　　求x=4和y=x^1/2，x軸所圍圖形繞x=6旋轉後得到的體積。

　　本例根據殼層法計算，如下圖所示：

　　殼層（或圓環）的高是x^1/2，半徑是6 – x，厚度是dx：

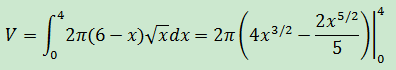
　　作者：我是8位的

　　出處：http://www.cnblogs.com/bigmonkey

　　本文以學習、研究和分享為主，如需轉載，請聯系本人，標明作者和出處，非商業用途！

數學筆記17——定積分的應用2（體積）