簡介：

割邊和割點的定義僅限於無向圖中。我們可以通過定義以蠻力方式求解出無向圖的所有割點和割邊,但這樣的求解方式效率低。Tarjan提出了一種快速求解的方式，通過一次DFS就求解出圖中所有的割點和割邊。

歡迎探討，如有錯誤敬請指正

如需轉載，請註明出處 http://www.cnblogs.com/nullzx/

1. 割點與橋（割邊）的定義

在無向圖中才有割邊和割點的定義

割點：無向連通圖中，去掉一個頂點及和它相鄰的所有邊，圖中的連通分量數增加，則該頂點稱為割點。

橋（割邊）：無向聯通圖中，去掉一條邊，圖中的連通分量數增加，則這條邊，稱為橋或者割邊。

割點與橋（割邊）的關系：

1）有割點不一定有橋,有橋一定存在割點

2）橋一定是割點依附的邊。

下圖中頂點C為割點，但和C相連的邊都不是橋。

2. 暴力解決辦法解決求解割點集和割邊集

暴力法的原理就是通過定義求解割點和割邊。在圖中去掉某個頂點，然後進行DFS遍歷，如果連通分量增加，那麽該頂點就是割點。如果在圖中去掉某條邊，然後進行DFS遍歷，如果連通分量增加，那麽該邊就是割邊。對每個頂點或者每個邊進行一次上述操作，就可以求出這個圖的所有割點和割邊，我們稱之為這個圖的割點集和割邊集。

在具體的代碼實現中，並不需要真正刪除該頂點和刪除依附於該頂點所有邊。對於割點，我們只需要在DFS前，將該頂點對應是否已訪問的標記置為ture，然後從其它頂點為根進行DFS即可。對於割邊，我們只需要禁止從這條邊進行DFS後，如果聯通分量增加了，那麽這條邊就是割邊。

3. Tarjan算法的原理

判斷一個頂點是不是割點除了從定義，還可以從DFS（深度優先遍歷）的角度出發。我們先通過DFS定義兩個概念。

假設DFS中我們從頂點U訪問到了頂點V（此時頂點V還未被訪問過），那麽我們稱頂點U為頂點V的父頂點，V為U的孩子頂點。在頂點U之前被訪問過的頂點，我們就稱之為U的祖先頂點。

顯然如果頂點U的所有孩子頂點可以不通過父頂點U而訪問到U的祖先頂點，那麽說明此時去掉頂點U不影響圖的連通性，U就不是割點。相反，如果頂點U至少存在一個孩子頂點，必須通過父頂點U才能訪問到U的祖先頂點，那麽去掉頂點U後，頂點U的祖先頂點和孩子頂點就不連通了，說明U是一個割點。

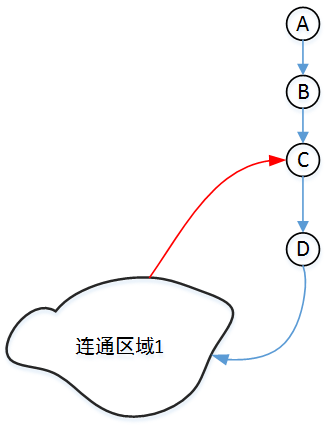
上圖中的箭頭表示DFS訪問的順序（而不表示有向圖），對於頂點D而言，D的孩子頂點可以通過連通區域1紅色的邊回到D的祖先頂點C（此時C已被訪問過），所以此時D不是割點。

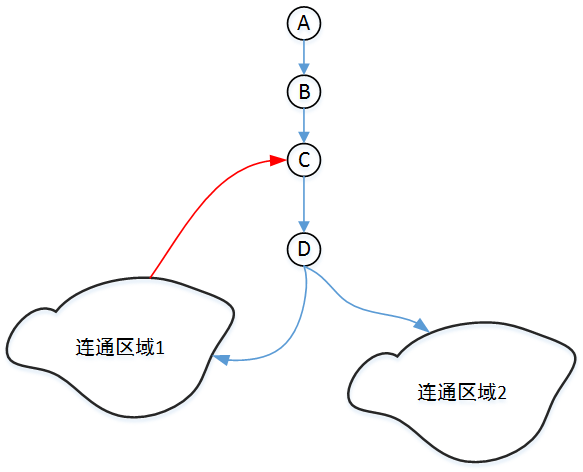
上圖中的連通區域2中的頂點，必須通過D才能訪問到D的祖先頂點，所以說此時D為割點。再次強調一遍，箭頭僅僅表示DFS的訪問順序，而不是表示該圖是有向圖。

這裏我們還需要考慮一個特殊情況，就是DFS的根頂點（一般情況下是編號為0的頂點），因為根頂點沒有祖先頂點。其實根頂點是不是割點也很好判斷，如果從根頂點出發，一次DFS就能訪問到所有的頂點，那麽根頂點就不是割點。反之，如果回溯到根頂點後，還有未訪問過的頂點，需要在鄰接頂點上再次進行DFS，根頂點就是割點。

4. Tarjan算法的實現細節

在具體實現Tarjan算法上，我們需要在DFS（深度優先遍歷）中，額外定義三個數組dfn[]，low[]，parent[]

1）dfn數組的下標表示頂點的編號，數組中的值表示該頂點在DFS中的遍歷順序(或者說時間戳)，每訪問到一個未訪問過的頂點，訪問順序的值（時間戳）就增加1。子頂點的dfn值一定比父頂點的dfn值大（但不一定恰好大1，比如父頂點有兩個及兩個以上分支的情況）。在訪問一個頂點後，它的dfn的值就確定下來了，不會再改變。

2） low數組的下標表示頂點的編號，數組中的值表示DFS中該頂點不通過父頂點能訪問到的祖先頂點中最小的順序值（或者說時間戳）。

每個頂點初始的low值和dfn值應該一樣，在DFS中，我們根據情況不斷更新low的值。

假設由頂點U訪問到頂點V。當從頂點V回溯到頂點U時，

如果

dfn[v] < low[u]

那麽

low[u] = dfn[v]

如果頂點U還有它分支，每個分支回溯時都進行上述操作，那麽頂點low[u]就表示了不通過頂點U的父節點所能訪問到的最早祖先節點。

現在我們來看一個例子，模仿程序計算各個頂點的dfn值和low值。下圖中藍色實線箭頭表示已訪問過的路徑，無箭頭虛線表示未訪問路徑。已訪問過的頂點用黃色標記，未訪問的頂點用白色標記，DFS當前正在處理的頂點用綠色表示。帶箭頭的藍色虛線表示DFS回溯時的返回路徑。

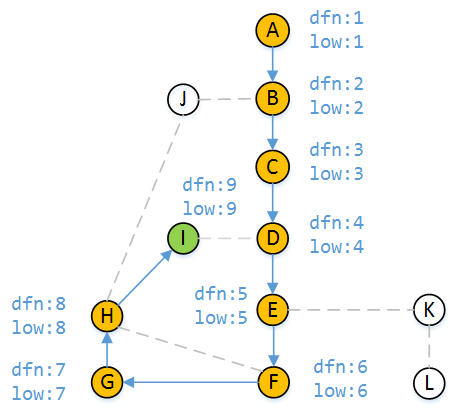
當DFS走到頂點H時，有三個分支，我們假設我們先走H-I，然後走H-F，最後走H-J。從H訪問I時，頂點I未被訪問過，所以I的dfn和low都為9。根據DFS的遍歷順序，我們應該從頂點I繼續訪問。

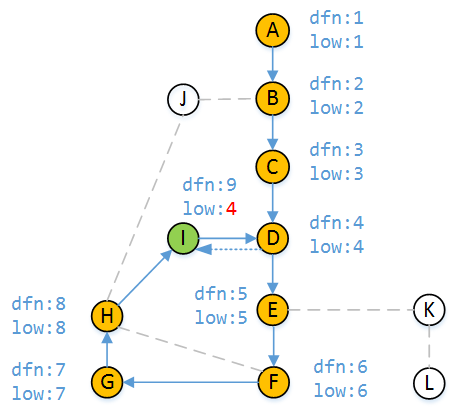
上圖表示由頂點I訪問頂點D，而此時發現D已被訪問，當從D回溯到I時，由於

dfn[D] < dfn[I]

說明D是I的祖先頂點，所以到現在為止，頂點I不經過父頂點H能訪問到的小時間戳為4。

Tarjan算法：求解圖的割點與橋（割邊）