什麽是排序穩定性？　　

　　通俗地講就是在排序前A的位置是 i ，B的位置是 j，此時 i < j，則如果在排序後A的位置還是在B之前，那麽稱它是穩定的。

它的好處是，如果排序算法是穩定的，那麽第一個排序結果可以為另一個排序所用。比如基數排序，先按低位排序，逐次按高位排序，低位相同的元素其順序在高位也相同時是不會改變的。

首先給出一張在前一個博客“時間復雜度入門理解”中出現過的一副圖，給出相關排序的穩定性：

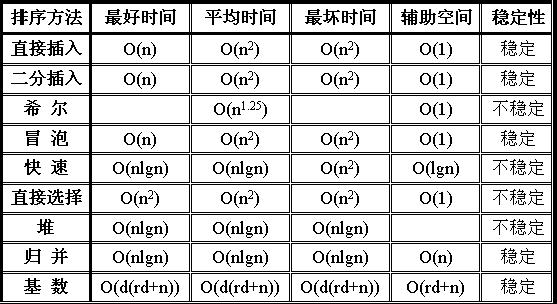
接下來，將解釋圖中某些排序是不穩定的的原因。

I）為什麽希爾排序不穩定？

A：首先要知道 Shell 排序是基於插入排序的優化排序，插入排序每次本身只能插入一位數據，希爾排序按照步長對多個元素進行插入排序。我們知道一次插入排序是穩定的，但是同時對多組數據進行插入排序，很明顯就穩定了，舉例：

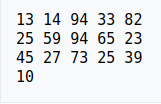
有這樣一組數：[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]

以第一輪是步長為5的希爾排序為例：

Before Shell Sort：

After Shell Sort：

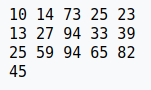
很明顯，之前 94 相對於 33 的位置就變了，這就是同時進行多次插入排序所導致的不穩定性。

II）為什麽快速排序不穩定？

A：快排的思想是先設一個中樞元素(也稱是基準數，對照用)，對兩遍進行排列，需要滿足左邊的元素都比中樞元素小，右邊元素都比中樞元素大，隨後對左和右的子序列也進行這樣的操作（分治）。而該排序不穩定的關鍵就是中樞元素在調換到序列中間的時候，會破壞了原來位於中央的元素的穩定性，比如有一個序列：

6 1 2 7 9 3 4 5 10 8 ,我們定義 6 為中樞元素

進行第一輪快排後，得3 1 2 5 4 6 9 7 10 8

這樣操作就會把 3 的穩定性破壞。所以快排是一個不穩定的排序算法，不穩定發生在中樞元素的交換時刻。

III）為什麽選擇排序是不穩定的？

A：選擇排序的操作是這樣：先在未排序的序列中選擇最小的元素（或最大的元素），把它放入第一個位置，再在剩余未排序序列中選擇第二小的，放在第二個位置...以此類推，直到所有序列排序完畢。但是，這樣直接讓最小元素與第一個位置上的元素進行交換，會破壞第一個元素的穩定性。

舉個例子：6 2 1 7 9 3 4 5 10 8

在6 和 1 的交換同時，6 與 2的穩定性就被破壞了。

IV）為什麽堆排序是不穩定的？

A：堆的結構是第 i 個結點的左子結點為 2i ，右子結點為2i + 1，子結點 i 的父結點的位置在 floor( (i-1)/2 ),最大堆要求父結點要大於它的兩個子結點，最小堆要求父結點要小於它的兩個子結點。而堆排序就是移除位於第一個數據的根結點，並做做大堆調整的遞歸運算。

在一個長為n的序列中，首先從第 n/2 個結點和其子結點一共三個結點開始選擇是最大堆還是最小堆，這三個元素的選擇當然並不會影響穩定性。但是之後第n/2 -1 ，n/2 -2， ... 2， 1 個結點開始選擇就會影響穩定性了。因為有可能第 n/2 -2 個父結點把其後的一個元素交換了，而第 n/2 -3 個父結點的後一個結點卻沒有被交換，那麽它們之間的穩定性就被破壞了。

註意

　　排序算法是否為穩定的是由具體算法決定的，不穩定的算法在某種條件下可以變為穩定的算法，而穩定的算法在某種條件下也可以變為不穩定的算法。比如冒泡，若讓交換的條件改成 r[j] >= r[j+1],兩個相等的記錄就會交換位置，從而變成不穩定的算法。

排序的穩定性