並查集 - 知乎專欄

POJ 1611(並查集+知識)

POJ 2524（並查集）

這個時候我們就希望重新設計一種數據結構，能夠高效的處理這三種操作，分別是

• MAKE-SET(x)，創建一個只有元素x的集合，且x不應出現在其他的集合中
• UNION(x, y)，將元素x所在集合Sx和元素y所在的集合Sy合並，這裏我們假定Sx不等於Sy
• FIND-SET(x)，查找元素x所在集合的代表

並查集的具體實現。

對於有根樹或者說森林的表示，可以用一個數組parent來實現。

parent[i]記錄元素i的父節點的編號，如果節點i本身就是根節點，那麽parent[i]就是-1。

MAKE-SET操作就是將parent數組賦值為-1，代碼比較簡單就不貼了。

UNION操作需要找到兩個元素的根，並把其中一個元素的根節點設置為另一個元素的根節點，其實就是調用了兩次FIND-SET，代碼如下

下面講一講並查集的具體實現。對於有根樹或者說森林的表示，可以用一個數組parent來實現。parent[i]記錄元素i的父節點的編號，如果節點i本身就是根節點，那麽parent[i]就是-1。MAKE-SET操作就是將parent數組賦值為-1，代碼比較簡單就不貼了。UNION操作需要找到兩個元素的根，並把其中一個元素的根節點設置為另一個元素的根節點，其實就是調用了兩次FIND-SET，代碼如下

再來說下FIND-SET這個操作的實現。首先有個很樸素的算法，對父節點遞歸調用FIND-SET，直到找到根為止。如果父節點是-1，那麽返回當前節點，否則遞歸調用查詢父親的根節點。代碼如下

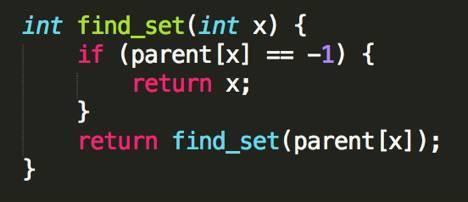
細心的同學會發現，如果我們這棵樹很深，那麽每次調用FIND-SET可能會需要O(n)的時間，總的復雜度在最壞情況下就是O(nQ)了，那不是更差了嗎？

這時候，我們就要引入路徑壓縮這個概念。什麽是路徑壓縮呢？就是在遞歸找到根節點的時候，把當前節點到根節點間所有節點的父節點都設置為根節點。舉個例子

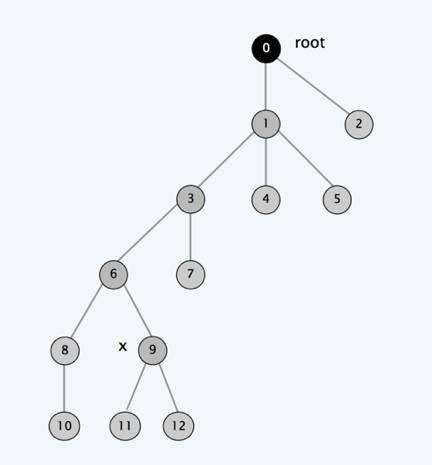
我們來看下圖，首先我們有個這樣的一棵樹，現在要找到元素9所在樹的根節點，在找根節點的過程中使用路徑壓縮，也就是說9到根的路徑上的節點9，6，3，1的父節點都設置成為根節點0，所以呢，在FIND-SET(9)之後，樹的形態就變成了下面的樣子

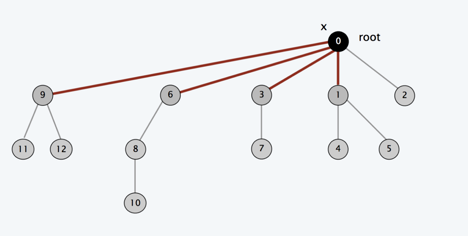
我們可以看到經過路徑壓縮的節點及其子樹到根節點的深度減小了很多，所以在以後的操作中，查找根節點的速度會快很多，平攤下來每次FIND-SET的操作幾乎是常數級別的。代碼也相當簡單，就只多了一句話

剛剛在合並的過程中，並沒有提到說到如何選取根，一般情況下兩個根節點隨意選取一個，如果需要更優的算法，可以按秩合並。除此以外，並查集還能處理帶權的情況，因為時間的關系就不在線上分享了。

算法 - 並查集