題目描述

「恒逸，你相信靈魂的存在嗎？」 郭恒逸和姚楓茜漫步在楓音鄉的街道上。望著漫天飛舞的紅楓，楓茜突然問出這樣一個問題。

「相信吧。不然我們是什麽，一團肉嗎？要不是有靈魂......我們也不可能再見到你姐姐吧。」 恒逸給出了一個略微無厘頭的回答。楓茜聽後笑了笑。 「那你仔細觀察過楓葉嗎？」 說罷，楓茜伸手，接住了一片飄落的楓葉。

「其實每一片楓葉都是有靈魂的。你看，楓葉上不是有這麽多脈絡嗎？我聽說，楓葉上有一些特殊的位置，就和人的穴位一樣。脈絡都是連接在這些穴位之間的。楓樹的靈魂流過每片楓葉的根部，沿著這些脈絡，慢慢漫進穴位，沁入整片楓葉。也是因為這個原因，脈絡才都是單向的，靈魂可不能倒著溜回來呢。」 恒逸似懂非懂地點了點頭。楓茜接著說了下去。

「正是因為有了靈魂，每片楓葉才會與眾不同。也正是因為有了靈魂，每片楓葉也都神似其源本的楓樹，就連脈絡也形成了一棵樹的樣子。但如果仔細看的話，會發現，在脈絡樹之外，還存在其它的非常細的脈絡。雖然這些脈絡並不在樹上，但他們的方向也同樣順著靈魂流淌的方向，絕不會出現可能使靈魂倒流的回路。」 恒逸好像突然想到了什麽。 「那這些脈絡豈不是可以取代已有的脈絡，出現在脈絡樹上？」 楓茜閉上了眼睛。

「是啊，就是這樣。脈絡樹並不是唯一的。只要有一些微小的偏差，脈絡樹就可能差之萬裏，哪怕是在這同一片楓葉上。就像我們的故事，結局也不是唯一的。只要改變一個小小的選項，故事流程可能就會被徹底扭轉。」

「真是深奧啊......」 恒逸盯著這片紅楓，若有所思地說。楓茜繼續說道。

「還不止如此呢。所有的脈絡都不會永恒存在，也不會永恒消失。不管是脈絡樹上的脈絡，還是之外的細小脈絡，都是如此。存在的脈絡可能斷開消失，消失的脈絡也可能再次連接。萬物皆處在永恒的變化之中，人與人之間的羈絆也是。或許有一天，我們與大家的羈絆也會如同脈絡一樣，被無情地斬斷。或許我們也終將成為”楓音鄉的過客“。或許這一切都會是必然，是楓樹的靈魂所決定的......」

楓茜的眼角泛起了幾滴晶瑩剔透的淚珠。恒逸看著這樣的楓茜，將她抱入懷中。

「別這樣想，楓茜。就算脈絡斷開，也有可能還會有新的脈絡樹，也還會與楓樹的根相連。這樣的話，我們的羈絆仍然存在，只是稍微繞了一些遠路而已。無論如何，我都不會離開你的。因為你是我窮盡一生所尋找的，我的真戀啊！」

兩人的目光對上了。楓茜幸福地笑了，把頭埋進了恒逸的懷抱。從遠方山上的楓林中，傳來了楓的聲音。

【問題描述】 不妨假設楓葉上有 n個穴位，穴位的編號為 1 ~ n。有若幹條有向的脈絡連接著這些穴位。穴位和脈絡組成一個有向無環圖——稱之為脈絡圖（例如圖 1），穴位的編號使得穴位 1 沒有從其他穴位連向它的脈絡，即穴位 1 只有連出去的脈絡；由上面的故事可知，這個有向無環圖存在一個樹形子圖，它是以穴位 1為根的包含全部n個穴位的一棵樹——稱之為脈絡樹（例如圖 2和圖 3給出的樹都是圖1給出的脈絡圖的子圖）；值得註意的是，脈絡圖中的脈絡樹方案可能有多種可能性，例如圖2和圖 3就是圖 1給出的脈絡圖的兩個脈絡樹方案。

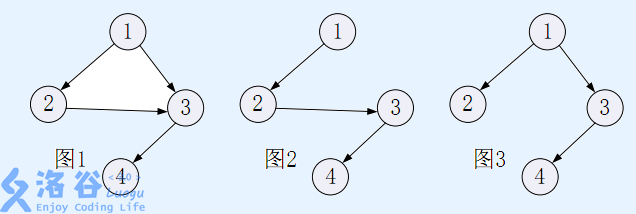
脈絡樹的形式化定義為：以穴位 r 為根的脈絡樹由楓葉上全部 n個穴位以及 n- 1 條脈絡組成，脈絡樹裏沒有環，亦不存在從一個穴位連向自身的脈絡，且對於楓葉上的每個穴位 s，都存在一條唯一的包含於脈絡樹內的脈絡路徑，使得從穴位r 出發沿著這條路徑可以到達穴位 s。 現在向脈絡圖添加一條與已有脈絡不同的脈絡（註意：連接 2個穴位但方向不同的脈絡是不同的脈絡，例如從穴位3到4的脈絡與從4到3的脈絡是不同的脈絡，因此，圖 1 中不能添加從 3 到 4 的脈絡，但可添加從 4 到 3 的脈絡），這條新脈絡可以是從一個穴位連向自身的（例如，圖 1 中可添加從 4 到 4 的脈絡）。原脈絡圖添加這條新脈絡後得到的新脈絡圖可能會出現脈絡構成的環。 請你求出添加了這一條脈絡之後的新脈絡圖的以穴位 1 為根的脈絡樹方案數。

由於方案可能有太多太多，請輸出方案數對 1,000,000,007 取模得到的結果。

輸入輸出格式

輸入格式：

輸入文件的第一行包含四個整數 n、m、x和y，依次代表楓葉上的穴位數、脈絡數，以及要添加的脈絡是從穴位 x連向穴位y的。 接下來 m行，每行兩個整數，由空格隔開，代表一條脈絡。第 i 行的兩個整數為ui和vi，代表第 i 條脈絡是從穴位 ui連向穴位vi的。

輸出格式：

輸出一行，為添加了從穴位 x連向穴位 y的脈絡後，楓葉上以穴位 1 為根的脈絡樹的方案數對 1,000,000,007取模得到的結果。

輸入輸出樣例

4 4 4 3
1 2
1 3
2 4
3 2

3

說明

對於所有測試數據，1 <= n <= 100000，n - 1 <= m <= min(200000, n(n -1) / 2)，

1 <= x, y, ui, vi <= n。

先不考慮圖中的環，讓每個點都選它的入點中的一個當爸爸，顯然答案是π indegree[i] 其中i>1。

然後特判一下如果y==1的話直接輸出就好了，因為在計算式裏這條邊對答案已經沒有貢獻了，並且在合法方案中這條邊肯定不能存在。

然後不合法的方案就是y到x的路徑上每一個點選的爸爸都是路徑上上一個點(y除外)，而且y的父親是x（這個是選附加邊帶來的效應）。

這樣的不合法的方案數就是除了這些節點的其他節點的入度的乘積(1除外)

所以在dag上dp就行了。。

#include<bits/stdc++.h>
#define ll long long
#define maxn 100005
#define ha 1000000007
using namespace std;
int n,m,to[maxn<<1|1],num;
int ne[maxn<<1|1],hd[maxn];
int S,T,id[maxn],ans=0;
int inv[maxn],cnt=1,f[maxn];
bool v[maxn];

inline void init(){
	inv[1]=1;
	for(int i=2;i<n;i++) inv[i]=-inv[ha%i]*(ll)(ha/i)%ha+ha;
}

inline int add(int x,int y){
	x+=y;
	return x>=ha?x-ha:x;
}

int dp(int x){
	if(v[x]) return f[x];
	v[x]=1;
	
	for(int i=hd[x];i;i=ne[i]) f[x]=add(f[x],dp(to[i]));
	f[x]=f[x]*(ll)inv[id[x]]%ha;
	return f[x];
}

int main(){
	scanf("%d%d%d%d",&n,&m,&S,&T);
	id[T]++,init();
	int uu,vv;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&uu,&vv);
		to[i]=vv,ne[i]=hd[uu],hd[uu]=i;
		id[vv]++;
	}
	
	for(int i=2;i<=n;i++) cnt=cnt*(ll)id[i]%ha;
	ans=cnt;
	
	if(S==T||T==1){
		printf("%d\n",ans);
		return 0;
	}
	
	v[S]=1,f[S]=inv[id[S]];
	dp(T);
	
    ans=add(ans,ha-cnt*(ll)f[T]%ha);
	
	printf("%d\n",ans);
	return 0;
}

[HNOI2015] 落憶楓音