1 貝葉斯方法

長久以來，人們對一件事情發生或不發生的概率，只有固定的0和1，即要麽發生，要麽不發生，從來不會去考慮某件事情發生的概率有多大，不發生的概率又是多大。而且概率雖然未知，但最起碼是一個確定的值。比如如果問那時的人們一個問題：“有一個袋子，裏面裝著若幹個白球和黑球，請問從袋子中取得白球的概率是多少？”他們會想都不用想，會立馬告訴你，取出白球的概率就是1/2，要麽取到白球，要麽取不到白球，即θ只能有一個值，而且不論你取了多少次，取得白球的概率θ始終都是1/2，即不隨觀察結果X 的變化而變化。

這種頻率派的觀點長期統治著人們的觀念，但是：

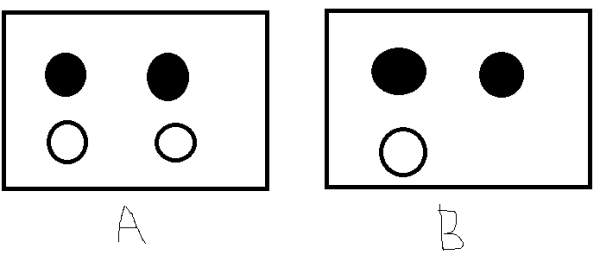
假設我們有如下的7個球在A,B兩個框中，如果我們隨便取一個球，已知取到的球來自B框中，那麽這個球是白球的概率是多少呢？或者問去除的球是白色，那麽取自B框的概率是多少呢？這個問題不是很好解決，直到後來一個名叫Thomas Bayes

1.1 貝葉斯方法的提出

托馬斯·貝葉斯Thomas Bayes（1702-1763）在世時，並不為當時的人們所熟知，很少發表論文或出版著作，與當時學術界的人溝通交流也很少，用現在的話來說，貝葉斯就是活生生一民間學術“屌絲”，可這個“屌絲”最終發表了一篇名為“An essay towards solving a problem in the doctrine of chances”，翻譯過來則是：機遇理論中一個問題的解。你可能覺得我要說：這篇論文的發表隨機產生轟動效應，從而奠定貝葉斯在學術史上的地位。

事實上，上篇論文發表後，在當時並未產生多少影響，在20世紀後，這篇論文才逐漸被人們所重視。對此，與梵高何其類似，畫的畫生前一文不值，死後價值連城。

回到上面的例子：“有一個袋子，裏面裝著若幹個白球和黑球，請問從袋子中取得白球的概率θ是多少？”貝葉斯認為取得白球的概率是個不確定的值，因為其中含有機遇的成分。比如，一個朋友創業，你明明知道創業的結果就兩種，即要麽成功要麽失敗，但你依然會忍不住去估計他創業成功的幾率有多大？你如果對他為人比較了解，而且有方法、思路清晰、有毅力、且能團結周圍的人，你會不由自主的估計他創業成功的幾率可能在80%以上。這種不同於最開始的“非黑即白、非0即1”的思考方式，便是貝葉斯式的思考方式。

繼續深入講解貝葉斯方法之前，先簡單總結下頻率派與貝葉斯派各自不同的思考方式：

• 頻率派把需要推斷的參數θ看做是固定的未知常數，即概率θ雖然是未知的，但最起碼是確定的一個值，同時，樣本X 是隨機的，所以頻率派重點研究樣本空間，大部分的概率計算都是針對樣本X 的分布；

• 而貝葉斯派的觀點則截然相反，他們認為參數θ是隨機變量，而樣本X 是固定的，由於樣本是固定的，所以他們重點研究的是參數θ的分布。

相對來說，頻率派的觀點容易理解，所以下文重點闡述貝葉斯派的觀點。

貝葉斯派既然把θ看做是一個隨機變量，所以要計算θ的分布，便得事先知道θ的無條件分布，即在有樣本之前（或觀察到X之前），θ有著怎樣的分布呢？

比如往臺球桌上扔一個球，這個球落會落在何處呢？如果是不偏不倚的把球拋出去，那麽此球落在臺球桌上的任一位置都有著相同的機會，即球落在臺球桌上某一位置的概率服從均勻分布。這種在實驗之前定下的屬於基本前提性質的分布稱為先驗分布，或的無條件分布。

至此，貝葉斯及貝葉斯派提出了一個思考問題的固定模式：

先驗分布 π(θ)+ 樣本信息χ? 後驗分布^π(θ|x)

上述思考模式意味著，新觀察到的樣本信息將修正人們以前對事物的認知。換言之，在得到新的樣本信息之前，人們對的認知是先驗分布 ^π(θ)，在得到新的樣本信息後χ，人們對θ的認知為^π(θ|x)。

而後驗分布^π(θ|x)一般也認為是在給定樣本χ的情況下θ的條件分布，而使達到最大的值稱為最大後^θMD驗估計，類似於經典統計學中的極大似然估計。

綜合起來看，則好比是人類剛開始時對大自然只有少得可憐的先驗知識，但隨著不斷是觀察、實驗獲得更多的樣本、結果，使得人們對自然界的規律摸得越來越透徹。所以，貝葉斯方法既符合人們日常生活的思考方式，也符合人們認識自然的規律，經過不斷的發展，最終占據統計學領域的半壁江山，與經典統計學分庭抗禮。

此外，貝葉斯除了提出上述思考模式之外，還特別提出了舉世聞名的貝葉斯定理。

1.2 貝葉斯定理

在引出貝葉斯定理之前，先學習幾個定義：

• 邊緣概率（又稱先驗概率）：某個事件發生的概率。邊緣概率是這樣得到的：在聯合概率中，把最終結果中那些不需要的事件通過合並成它們的全概率，而消去它們（對離散隨機變量用求和得全概率，對連續隨機變量用積分得全概率），這稱為邊緣化（marginalization），比如A的邊緣概率表示為P(A)，B的邊緣概率表示為P(B)。

• 聯合概率表示兩個事件共同發生的概率。A與B的聯合概率表示為P(A∩B)或者P(A,B)。

• 條件概率（又稱後驗概率）：事件A在另外一個事件B已經發生條件下的發生概率。條件概率表示為P(A|B)，讀作“在B條件下A的概率”,。

接著，考慮一個問題：P(A|B)是在B發生的情況下A發生的可能性。

• 首先，事件B發生之前，我們對事件A的發生有一個基本的概率判斷，稱為A的先驗概率，用P(A)表示；

• 其次，事件B發生之後，我們對事件A的發生概率重新評估，稱為A的後驗概率，用P(A|B)表示；

• 類似的，事件A發生之前，我們對事件B的發生有一個基本的概率判斷，稱為B的先驗概率，用P(B)表示；

• 同樣，事件A發生之後，我們對事件B的發生概率重新評估，稱為B的後驗概率，用P(B|A)表示。

貝葉斯定理便是基於下述貝葉斯公式：

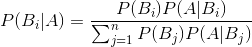
P(A|B)=P(B|A)P(A)/P(B)

上述公式的推導其實非常簡單，就是從條件概率推出。

根據條件概率的定義，在事件B發生的條件下事件A發生的概率是

P(A|B)=P(A∩B)/P(B)

同樣地，在事件A發生的條件下事件B發生的概率

P(B|A)=P(A∩B)/P(A)

整理與合並上述兩個方程式，便可以得到：

P(A|B)P(B)=P(A∩B)=P(B|A)P(A)

接著，上式兩邊同除以P(B)，若P(B)是非零的，我們便可以得到貝葉斯定理的公式表達式：

P(A|B)=P(B|A)*P(A)/P(B)

筆者在看《從貝葉斯方法談到貝葉斯網絡》的時候，看到這裏，其實已經暈暈的了。

P(A|B) 和 P(B|A) 之類的經常讓人混淆，@待字閨中的陳老師給出了理解的一個關鍵點，區分出規律和現象，就是將A看成“規律”，B看成“現象”，那麽貝葉斯公式看成：

陳老師在《這的理解貝葉斯公式嗎》和《又一個生活中的貝葉斯應用》給出了幾個通俗易懂的例子，這裏不再贅述。

貝葉斯推斷的含義

然後搜下，發現其實還有更好闡釋，比如

對條件概率公式進行變形，可以得到如下形式：

我們把P(A)稱為"先驗概率"（Prior probability），即在B事件發生之前，我們對A事件概率的一個判斷。P(A|B)稱為"後驗概率"（Posterior probability），即在B事件發生之後，我們對A事件概率的重新評估。P(B|A)/P(B)稱為"可能性函數"（Likelyhood），這是一個調整因子，使得預估概率更接近真實概率。

所以，條件概率可以理解成下面的式子：

後驗概率　＝　先驗概率 ｘ 調整因子

這就是貝葉斯推斷的含義。我們先預估一個"先驗概率"，然後加入實驗結果，看這個實驗到底是增強還是削弱了"先驗概率"，由此得到更接近事實的"後驗概率"。

在這裏，如果"可能性函數"P(B|A)/P(B)>1，意味著"先驗概率"被增強，事件A的發生的可能性變大；如果"可能性函數"=1，意味著B事件無助於判斷事件A的可能性；如果"可能性函數"<1，意味著"先驗概率"被削弱，事件A的可能性變小。

貝葉斯定理應用示例:

已知某種疾病的發病率是0.001，即1000人中會有1個人得病。現有一種試劑可以檢驗患者是否得病，它的準確率是0.99，即在患者確實得病的情況下，它有99%的可能呈現陽性。它的誤報率是5%，即在患者沒有得病的情況下，它有5%的可能呈現陽性。現有一個病人的檢驗結果為陽性，請問他確實得病的可能性有多大？

假定A事件表示得病，那麽P(A)為0.001。這就是"先驗概率"，即沒有做試驗之前，我們預計的發病率。再假定B事件表示陽性，那麽要計算的就是P(A|B)。這就是"後驗概率"，即做了試驗以後，對發病率的估計。

根據條件概率公式，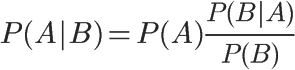

用全概率公式改寫分母，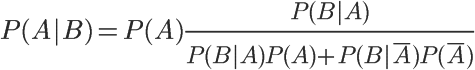

將數字代入，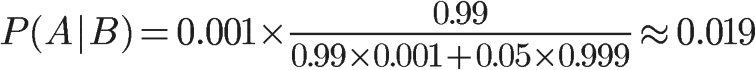

我們得到了一個驚人的結果，P(A|B)約等於0.019。也就是說，即使檢驗呈現陽性，病人得病的概率，也只是從0.1%增加到了2%左右。這就是所謂的"假陽性"，即陽性結果完全不足以說明病人得病。

或許換成這個公式 P(A|B)=P(A∩B)/B，看起來更加直白寫：

闡釋：

如果沒有誤報，那麽得病率：.001*.99

如果是誤報，那麽得病率為：.05*(1-.0001)，

所以：

p(A|B)=.001*.99/[.99*.001+.05*(1-.0001)]=.019

為什麽會這樣？為什麽這種檢驗的準確率高達99%，但是可信度卻不到2%？答案是與它的誤報率太高有關。

（【習題】如果誤報率從5%降為1%，請問病人得病的概率會變成多少？）

有興趣的朋友，還可以算一下"假陰性"問題，即檢驗結果為陰性，但是病人確實得病的概率有多大。然後問自己，"假陽性"和"假陰性"，哪一個才是醫學檢驗的主要風險？

再來一個類似案例：https://www.zhihu.com/question/21134457/answer/169523403

一種癌癥，得了這個癌癥的人被檢測出為陽性的幾率為90%，未得這種癌癥的人被檢測出陰性的幾率為90%，而人群中得這種癌癥的幾率為1%，一個人被檢測出陽性，問這個人得癌癥的幾率為多少？

猛地一看，被檢查出陽性，而且得癌癥的話陽性的概率是90%，那想必這個人應該是難以幸免了。那我們接下來就算算看。

我們用 A 表示事件 “測出為陽性”, 用 B1 表示“得癌癥”, B2表示“未得癌癥”。根據題目，我們知道如下信息:

P(B1)=.01

P(B2)=.99

P(A|B1)=.9

P(A|B2)=.1

那麽我們現在想得到的是陽性的情況下，得癌癥的幾率

P(B1,A)=P(B1)*P(A|B1)=.01*.09=0.009;

這裏P(B1,A)表示的是聯合概率，得癌癥且檢測出陽性的概率是人群中得癌癥的概率乘上得癌癥時測出是陽性的幾率，是0.009。同理可得得癌癥且檢測出陽性的概率：

P(B2,A)=P(B2)*P(A|B2)=.99*.1=.099;

這個概率是什麽意思呢？其實是指如果人群中有1000個人，檢測出陽性並且得癌癥的人有9個，檢測出陽性但未得癌癥的人有99個。可以看出，檢測出陽性並不可怕，不得癌癥的是絕大多數的，這跟我們一開始的直覺判斷是不同的！可直到現在，我們並沒有得到所謂的“在檢測出陽性的前提下得癌癥的 概率 ”，怎麽得到呢？很簡單，就是看被測出為陽性的這108(9+99)人裏，9人和99人分別占的比例就是我們要的,也就是說我們只需要添加一個歸一化因子(normalization)就可以了。

所以陽性得癌癥的概率 P(B1|A)= .009/(.099+.009)≈.083,

陽性未得癌癥的概率 P(B2|A)= .099/(.099+.009)≈.917 。

這裏 P(B1|A),P(B2|A)中間多了這一豎線 成為了條件概率，而這個概率就是貝葉斯統計中的 後驗概率！而人群中患癌癥與否的概率 P(B1),P(B2) 就是 先驗概率！我們知道了先驗概率，根據觀測值(observation)，也可稱為test evidence：是否為陽性，來判斷得癌癥的後驗概率，這就是基本的貝葉斯思想，我們現在就能得出本題的後驗概率的公式為：

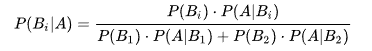
由此就能得到如下的貝葉斯公式的一般形式。

我們把上面例題中的 A 變成樣本(sample) x , 把 B 變成參數(parameter) \theta , 我們便得到我們的貝葉斯公式：

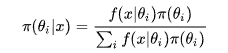
可以看出上面這個例子中，B 事件的分布是離散的，所以在分母用的是求和符號 Σ 。那如果我們的參數θ的分布是連續的呢？沒錯，那就要用積分，於是我們終於得到了真正的 貝葉斯公式 ：

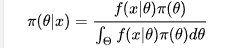
其中π指的是參數的概率分布，π(θ)指的是先驗概率，π(θ|x)指的是後驗概率， 指的是我們觀測到的樣本的分布，也就是似然函數(likelihood)，記住豎線 | 左邊的才是我們需要的。其中積分求的區間Θ指的是參數 θ 所有可能取到的值的域，所以可以看出後驗概率π(θ|x) 是在知道 X的前提下在 Θ域內的一個關於 θ 的概率密度分布，每一個θ都有一個對應的可能性(也就是概率)。

作者：徐炎琨

鏈接：https://www.zhihu.com/question/21134457/answer/169523403

來源：知乎

著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請註明出處。

一個更好理解的例子：

鏈接：https://www.zhihu.com/question/51448623/answer/175907274

假設你是一個領導者，或者說，山寨的頭目好了。

你是遠近聞名的土匪頭子。哈哈

聽聞最近官兵換統領了，可能要來剿匪了。這裏駐紮的軍兵每5年都會換一屆統領，新官上任三把火，都想拿你們來開刀。不過每次，你都帶領兄弟們打退了官兵的圍剿。

這次不同了，聽說換的是個厲害的角色。因此，你讓二頭領派人下山去打探消息，看看是不是要來攻山。

打探的人回來了，支支吾吾地說：官兵不會來，因為新來統領他媽生病了，回家探病去了。

你這個時候，信不信他的話？

你看這個回報的人，變毛變色的，說話吞吞吐吐。但是，他也有可能是因為沒見過你大頭領，回話的時候，有些緊張害怕。

你作為一個受過高等教育的人（學過概率論，貝葉斯定理的人），心理開始盤算：

1. 官兵每5年來一次，那麽今年來的概率就是

1/5=20%

2. 派出去打探的這小子，說官兵不會來，那麽今年來的概率是：

0

3. 嗯？派出去這小子，是不是可靠，不會說的是假話吧？

於是，你向旁人了解了一下：

1. 三頭領勸你好好考慮下，說這個小子雖然人機靈，但是經常是十句話裏面有七八句是假的，嘴裏沒實話。

於是你心理又開始盤算：

1. 十之七八都假話？能嗎？

2.姑且認為三當家的話是真的。

3.那麽派出去這小子，說假話的概率就是 70%~80%：

就按75%算把，

說真話的概率就是25%

4.那麽如果他說的真話：

他說官兵不來，官兵就不來的概率是：25%*80%=20%

他說官兵來 ， 官兵就來的概率是 ：25%*20%=5%

5. 如果他說的假話:

他說官兵不來，官兵 來的概率是：75%*20%=15%

他說官兵來 ，官兵不來的概率是：75%*80%=60%

6. 那麽他這次口口聲聲說了：官兵不來

那麽根據5.的結果：

官兵來的概率是 15%

官兵不來的概率是 20%

比率是： 來/不來=15/20=3/4

也就是說，來的概率是3/7 =42.86% 不來的概率是4/7=57.14%

【註意】：貝葉斯定律是直接將 15%+20%做分母，兩個概率做分子，分別重新計算其條件概率。

對你一個決策者來說，這樣的比率，太高，顯然沒有什麽意義：

於是你決定再派一個自己的親信兄弟下去打探：

三天後回來，回報結果還和剛才結果一樣：官兵不會來，統領回家了。

這次是你的親信。應該將概率一下子修正為：

官兵來：0 官兵不來 100%

但是，這個親信，雖然忠誠，明顯不夠機靈。他在打探時，可能被欺騙。他雖然不會騙你，但難保他被別人騙。因此，他的話只能做參考，也不可完全相信：

0.參照之前那個兄弟的結果：

3/7來，4/7不來

1.考慮你的親信被欺騙的概率為 30%

2.那麽同樣：

他被騙：

他說官兵不來，官兵不來的概率是：3/7*30%=12.86%（實際官兵會來）

他說官兵來， 官兵來的概率是 ：4/7*30%=17.14%

他沒被騙：

他說官兵不來，官兵不來的概率是：4/7*70%=40%（實際官兵不會來）

他說官兵來， 官兵來的概率是 ：3/7*70%=30%

3. 於是他向你報告官兵不來，那麽：

來/不來=12.86/40

於是官兵來的概率就是

12.86/（12.86+40）=20.46%

看到20.46%？這個概率還是太大，你還是不放心，決定帶上二當家，自己親自下山一趟。

於是你門分頭走街串巷，茶館酒肆裏轉悠，四處打探。

最後，還是得出相同的結果。

於是你將結果修正為：

官兵來的概率：0，不來的概率：100%

最後你和二當家在一家酒館碰頭：

你說，官兵不來

二當家說：我看不一定，我摸到了官兵駐紮的地方，看到了官兵在演習調動。

聽了這個消息，你大驚失色。你感覺自己可能也被騙了，但是憑自己的經驗，被騙的可能性很小只有5%的可能性。

於是，你和二當家，約定今晚，趁著月色又摸來了一趟軍營。發現確實在調動軍隊。

你心裏想：我的乖乖，幸虧過來看了看，否則都沒準備，就被官兵包餃子了。

你一下子，又將概率修正為：

官兵來：100%，官兵不來：0

仔細觀察了一下動靜，聽了聽。軍營裏有人小聲說話，你和二當家趴在外面聽：

士兵甲：哎？老四，你知道這回咱們要調哪裏去？

士兵乙：那我哪裏知道，那是上頭的事情。

士兵甲：嘿！我勸你，把你那點銀子趁早寄回家去吧。再晚，怕是沒機會了。

士兵乙：老三，你瞎說啥，你知道啥，又要打清風寨？

士兵甲：嘿，打啥清風寨啊。要打打仗了。

你心裏想，不打你們山寨？打什麽打仗？最近有啥大事？於是你又將那個心理的概率修正為：

官兵來：0%，官兵不來：100%

這個時候，你突然意識到，自己的思維好像不太對。這後面幾次，信息全是壓倒性的修正，一次一次，不是0%就是100%，完全不像一個受過高等教育的山寨頭領。

於是，你默默地多計算了兩步。假設這個士兵說真話的概率為50%，那麽他說官兵不去，

那麽，結合剛剛的概率（來的概率：20.46%，不來的概率：79.54%）

1. 他說真話 ：

他說官兵不來，官兵不來的概率是：79.54%*50%=39.77%（實際官兵會來）

他說官兵來， 官兵來的概率是 ：20.46%*50%=10.23%

2.他說假話：

他說官兵來，官兵不來的概率是：20.46*50%=10.23%（實際官兵不會來）

他說官兵不來，官兵來的概率是 ：79.54%*50%=39.77%

3.最終算出來，官兵來的概率是：

20.46%

你發現，概率居然沒變？你明白了，你假設說真話的概率為50%，那相當於沒有任何信息量，等於他什麽也沒說。媽*的！你作為受過高等教育的土匪頭子，還是情不自禁地罵了一句。

於是你接著聽

士兵甲接著說：嘿嘿，皇帝老子要打臺灣了。收拾了三藩，接下來收拾臺灣了，我們都歸施瑯統領。

士兵乙：真的假的，這你清楚？瞎掰吧？

士兵甲：嗨，我騙你做啥？今天我聽李二嘎子說的，他說他二叔在施瑯手下，他二叔告訴他的。

士兵乙：呵呵，李二嘎子的話你也信，那家夥，十句有兩句是假話，你信他？

.....

你聽到這裏，已經敏銳的覺察到事情的原理了，朝著二當家使了個眼色，你們悄悄撤了。

為什麽？因為你算了一下，李二嘎子的話可信嗎？根據士兵乙的估計這個人，話裏80%真話，20%假話，於是你開始計算了：

1.李二嘎子說真話：

他說官兵要打臺灣不來，那麽官兵真不來： 80%*79.54%=63.63%

他說官兵不打臺灣要來，那麽官兵要來 ：80%*20.46%=16.37%

2.李二嘎子說假話

他說官兵要打臺灣不來，那麽官兵要來 ： 20%*20.46%=4.09%

他說官兵不打臺灣要來，那麽官兵不來 ：20%*79.54%=15.91%

3.綜合下來，官兵要來的概率是

4.09%/（4.09%+63.63%）=6.04%

看樣子，官兵不來的概率很大。但是也不能掉以輕心。所以，你決定，回去之後，不必過份緊張，但要提高警戒，並不斷派兄弟下來打探情況。

這樣看來，應該是可以決策了把。。。

而做決策，就是根據貝葉斯定律，不斷用後驗概率來修正先驗概率的吧。

轉載請註明來處，文章首發：貝葉斯公式由淺入深大講解-AI基礎算法入門 - math，數學專欄 - 周陸軍的個人網站

參考文章：

從貝葉斯方法談到貝葉斯網絡

Chapter 1 貝葉斯推斷的思想

全棧必備 貝葉斯方法

真的理解貝葉斯公式嗎？

全概公式和貝葉斯公式的理解

貝葉斯推斷及其互聯網應用（一）：定理簡介

機器學習(一) —— 淺談貝葉斯和MCMC（推薦閱讀）

貝葉斯公式由淺入深大講解—AI基礎算法入門