本文介紹了線性混合效應模型的新型貝葉斯分析。該分析基於部分折疊的方法，該方法允許某些組件從模型中部分折疊。得到的部分折疊的Gibbs（PCG）采樣器被構造成適合線性混合效應模型，預計會比相應的Gibbs采樣器表現出更好的收斂特性。為了構建PCG采樣器而不使組件更新復雜化，我們考慮通過在線性混合效應模型中根據組內方差表示組間方差來重新參數化模型組件。

簡介

已經開發出混合效應模型來處理相關響應數據並考慮多種變化來源。為了解釋響應變量的依賴結構，混合效應模型不僅包含固定效應，還包含將某些協變量視為隨機變量的隨機效應。混合效應模型在一段時間內對受試者進行重復測量的環境中特別方便。與傳統的縱向數據方法相比，混合效應模型也可以處理缺失值。

方法 具有適當先驗分布的混合效應模型考慮一般的混合效應模型

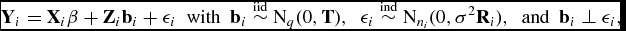（1）

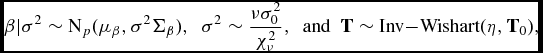（2）

其中b=（b1，b2，...，bk）是隨機效應的q×k矩陣，Y= {Yi}ki= 1是觀測數據的集合，代表逆Wishart分布，和

默頓的跳躍擴散模型

考慮默頓的跳躍擴散模型其目的是模型跳躍由於罕見的經濟事件或新聞突然資產價格。該模型由。給出

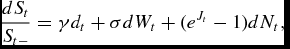（3）

其中St代表時間t的資產價格，γ是資產的瞬時預期收益，σ是資產收益的瞬時標準差，Wt是維納過程，對數跳躍大小Jt是均值μ高斯隨機變量?和方差σ2?，和?噸是一個泊松過程與到達速率λ。在沒有跳躍過程的情況下，（3）中的模型被稱為幾何布朗運動過程，並且{St}Tt= 1的連續對數比率與平均γ和方差σ獨立高斯隨機變量2。然而，當在時間t發生跳躍時，該過程不再是連續的; S t -明確表示跳轉之間的不連續性。此外，我們考慮基於日常的資產價格，因此假設在每個時間間隔內最多發生一次跳躍，即

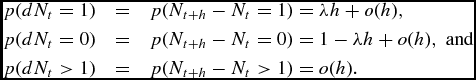
模擬

為了說明PCG采樣器相對於Gibbs采樣器的改進收斂特性，對具有適當先驗分布的混合效應模型和Merton的跳躍擴散模型進行了仿真研究。首先，在（7）中具有適當先驗分布的混合效應模型中，我們假設存在k = 100個組，並且每個組具有相同的大小n i = 2.模型參數的真實值被設置為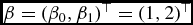，σ 2 = 1，並且

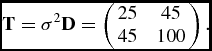
圖1由具有適當先驗分布的混合效應模型構建的Gibbs采樣器模擬的每個模型參數的混合圖，自相關圖和邊際後驗概率分布函數。

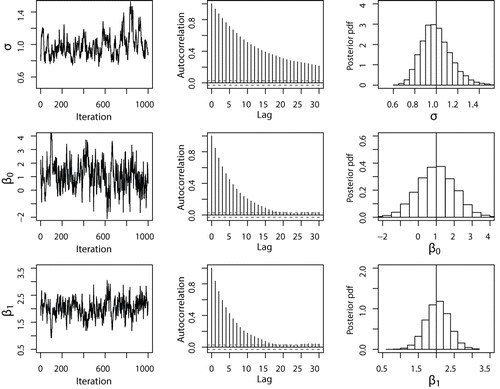
圖2由具有適當先驗分布的混合效應模型構建的PCG采樣器模擬的每個模型參數的混合圖，自相關圖和邊際後驗概率分布函數。

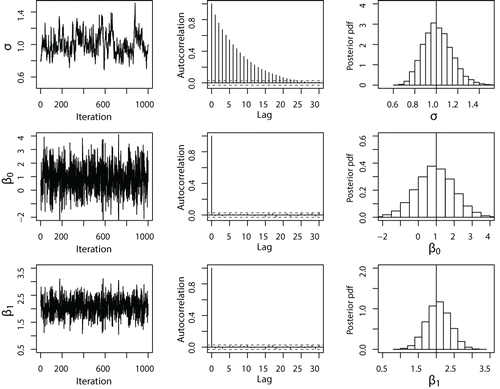
圖3由具有適當先驗分布的Merton跳躍擴散模型構建的Gibbs采樣器模擬的每個模型參數的混合圖，自相關圖和邊際後驗概率分布函數。

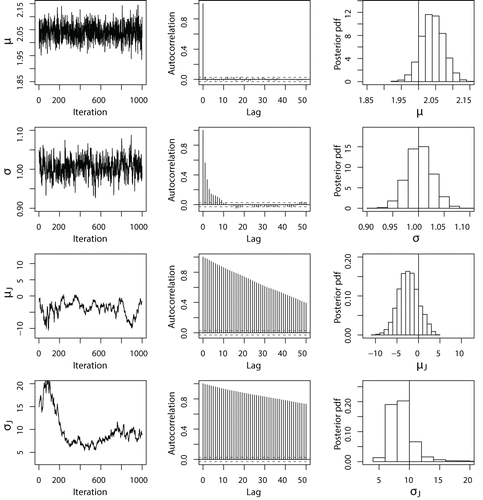
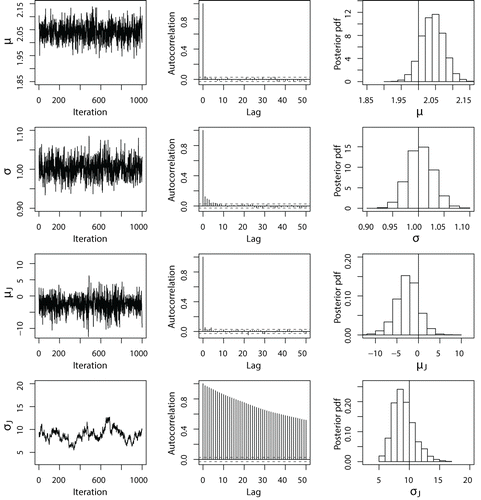
圖4由具有適當先驗分布的Merton跳躍擴散模型構建的PCG采樣器模擬的每個模型參數的混合圖，自相關圖和邊際後驗概率分布函數。

適用於睡眠剝奪研究為了說明所提方法在實際數據問題中的優勢，混合效應模型適用於睡眠剝奪的縱向數據。睡眠限制和隨後恢復期間性能退化和恢復的模式：睡眠劑量 - 反應研究。。在睡眠剝奪研究中，對18名長途卡車司機進行了一系列測試的平均反應時間（以毫秒為單位），從第1天到第9天，他們被限制為每晚3小時的睡眠。在第0天，平均在從23:00到07:00睡眠8小時後測量反應時間。圖5主體內系數和混合效應系數的比較。空心圓圈表示固定效應系數的估計值，實心圓圈表示受試者內系數的估計值，閉合三角形表示由R包lme4計算的混合效應估計值，實心方塊表示由PCG采樣器計算的混合效應估計值，以及箭頭表示受試者內固定效應和混合效應模型之間估計值的變化。

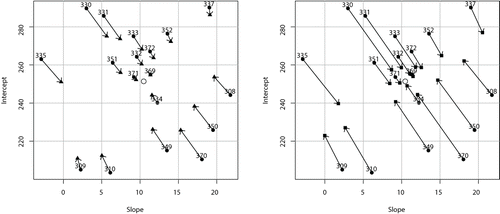
圖6混合效應系數的後驗分布。閉環表示受試者內固定效應系數的估計，閉合三角表示由R包lme4計算的混合效應估計，而閉合正方形表示由PCG采樣器計算的混合效應估計。

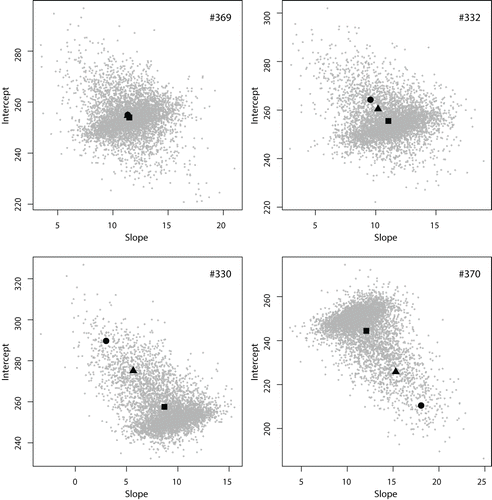
圖7帶有觀測數據的擬合線性線。

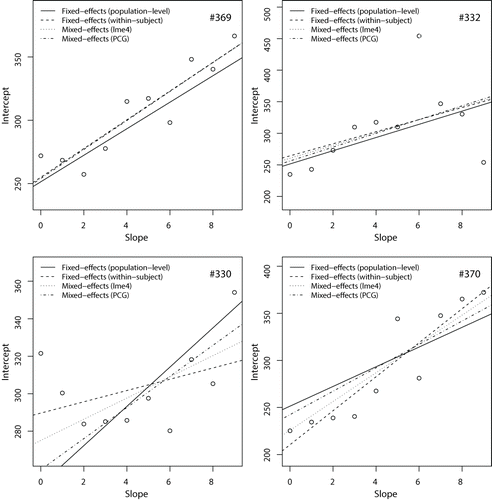
討論

本文提出了線性混合效應模型的有效貝葉斯分析的部分折疊方法。這種方法的核心是混合效應模型的新參數化的公式，它可以應用部分折疊，而不會使得到的PCG采樣器中的組件更新復雜化。結果表明，一般混合效應模型和默頓跳躍擴散模型的PCG采樣大大提高了相應Gibbs采樣器的收斂性。

線性混合效應模型Linear Mixed-Effects Models的部分折疊Gibbs采樣