verilog乘法器的設計
阿新 • • 發佈:2018-08-16
一個 http 乘法 代碼 pos 判斷 大於 初始 inpu
在verilog編程中,常數與寄存器變量的乘法綜合出來的電路不同於寄存器變量乘以寄存器變量的綜合電路。知乎裏的解釋非常好https://www.zhihu.com/question/45554104,總結乘法器模塊的實現https://blog.csdn.net/yf210yf/article/details/70156855
乘法的實現是移位求和的過程
乘法器模塊的實現主要有以下三種方法
1.串行實現方法
占用資源最多,需要的時鐘頻率高些,但是數據吞吐量卻不大
兩個N位二進制數x、y的乘積用簡單的方法計算就是利用移位操作來實現。
其框圖如下:
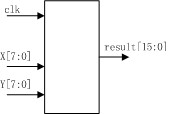
其狀態圖如下:
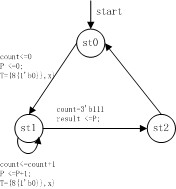
代碼:
module multi_CX(clk, x, y, result);02 03 input clk; 04 input [7:0] x, y; 05 output [15:0] result; 06 07 reg [15:0] result; 08 09 parameter s0 = 0, s1 = 1, s2 = 2; 10 reg [2:0] count = 0; 11 reg [1:0] state = 0; 12 reg [15:0] P, T; 13 reg [7:0] y_reg; 14 15 always @(posedge clk) begin 16 case (state)17 s0: begin 18 count <= 0; 19 P <= 0; 20 y_reg <= y; 21 T <= {{8{1‘b0}}, x}; 22 state <= s1; 23 end 24 s1: begin 25 if(count == 3‘b111) 26 state<= s2; 27 else begin 28 if(y_reg[0] == 1‘b1) 29 P <= P + T; 30 else 31 P <= P; 32 y_reg <= y_reg >> 1; 33 T <= T << 1; 34 count <= count + 1; 35 state <= s1; 36 end 37 end 38 s2: begin 39 result <= P; 40 state <= s0; 41 end 42 default: ; 43 endcase 44 end 45 46 endmodule
慢速信號處理中常用到的。
2.並行流水線實現方法
將操作數的N位並行提交給乘法器,這種方法並不是最優的實現架構,在FPGA中進位的速度遠大於加法的速度,因此將相臨的寄存器相加,相當於一個二叉樹的結構,實際上對於n位的乘法處理,需要logn級流水來實現。
一個8位乘法器,其原理圖如下圖所示:
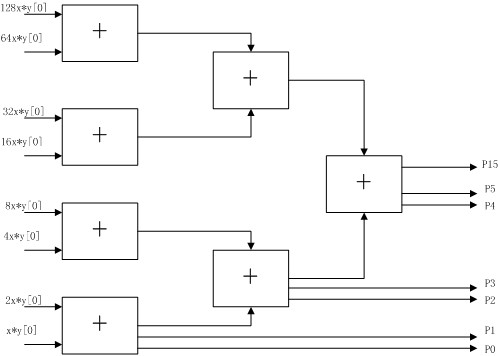
其實現的代碼如下:
module multi_4bits_pipelining(mul_a, mul_b, clk, rst_n, mul_out); input [3:0] mul_a, mul_b; input clk; input rst_n; output [15:0] mul_out; reg [15:0] mul_out; reg [15:0] stored0; reg [15:0] stored1; reg [15:0] stored2; reg [15:0] stored3; reg [15:0] stored4; reg [15:0] stored5; reg [15:0] stored6; reg [15:0] stored7; reg [15:0] mul_out01; reg [15:0] mul_out23; reg [15:0] add01; reg [15:0] add23; reg [15:0] add45; reg [15:0] add67; always @(posedge clk or negedge rst_n) begin if(!rst_n) begin mul_out <= 0; stored0 <= 0; stored1 <= 0; stored2 <= 0; stored3 <= 0; stored4 <= 0; stored5 <= 0; stored6 <= 0; stored7 <= 0; add01 <= 0; add23 <= 0; add45 <= 0; add67 <= 0; end else begin stored0 <= mul_b[0]? {8‘b0, mul_a} : 16‘b0; stored1 <= mul_b[1]? {7‘b0, mul_a, 1‘b0} : 16‘b0; stored2 <= mul_b[2]? {6‘b0, mul_a, 2‘b0} : 16‘b0; stored3 <= mul_b[3]? {5‘b0, mul_a, 3‘b0} : 16‘b0; stored4 <= mul_b[0]? {4‘b0, mul_a, 4‘b0} : 16‘b0; stored5 <= mul_b[1]? {3‘b0, mul_a, 5‘b0} : 16‘b0; stored6 <= mul_b[2]? {2‘b0, mul_a, 6‘b0} : 16‘b0; stored7 <= mul_b[3]? {1‘b0, mul_a, 7‘b0} : 16‘b0; add01 <= stored1 + stored0; add23 <= stored3 + stored2; add45 <= stored5 + stored4; add67 <= stored7 + stored6; mul_out01 <= add01 + add23; mul_out23 <= add45 + add67; mul_out <= mul_out01 + mul_out23; end end endmodule
流水線乘法器比串行乘法器的速度快很多很多,在非高速的信號處理中有廣泛的應用。至於高速信號的乘法一般需要利用FPGA芯片中內嵌的硬核DSP單元來實現。
3.booth算法
看了原文獻,有基2和基4兩種實現
最常用的主要還是基2實現也就是用被除數的每兩位做編碼,Booth算法對乘數從低位開始判斷,根據兩個數據位的情況決定進行加法、減法還是僅僅移位操作。判斷的兩個數據位為當前位及其右邊的位(初始時需要增加一個輔助位0),移位操作是向右移動。
在Booth算法中,操作的方式取決於表達式(y【i+1】-y【i】)的值,這個表達式的值所代表的操作為: 0 無操作 +1 加x -1 減x Booth算法操作表示 yi yi+1 操作 說明 0 0 無 處於0串中,不需要操作 0 1 加x 1串的結尾 1 0 減x 1串的開始 1 1 無 處於1串中,不需要操作 乘法過程中,被乘數相對於乘積的左移操作可表示為乘以2,每次循環中的運算可表示為對於x(y(i+1)-yi)2^31-i項的加法運算(i=3l,30,…,1,0)。這樣,Booth算法所計算的結果 可表示為: x×(0-y31)×2^0 +x×(y31-y30)×2^1 +x×(y30-y29)×2^2 … +x×(y1-y0)×2^31 [1] =x×(-y0×2^31 +y1×2^30 +y2×2^29+.......+y31×2^0) =x×y代碼
module booth( start_sig, a, b, done_sig , product) wire [1:0] start_sig; wire [7:0] a; wire [7:0] b; wire [15:0] product; /********************************/ reg[3:0] i; reg[7:0] ra; reg[7:0] rs; reg[16:0] rp; reg[3:0] x; reg isdone; always @(posedge clk or negedge rst_n) if(!rst_n) begin i<=4‘d0; ra<=8‘d0; rs<=8‘d0; rp<=17‘d0; x<=4‘d0; isdone<=1‘b0; end else if(start_sig) case(i) 0: begin ra<=a; rs<=(~a+1); rp<={8‘d0,b,1‘b0}; i<=i+1; end 1: if(x==8) begin x<=4‘d0; i<=i+2; end else if(rp[1:0]==2‘b01) begin rp<={rp[16:9]+ra,rp[8:0]}; i<=i+1; end else if(rp[1:0]==2‘b10) begin rp<={rp[16:9]+rs,rp[8:0]}; i<=i+1; end else i<=i+1; 2: begin rp<={rp[16],rp[16:1]}; x<=x+1;//返回去檢測對應寄存器值的方法 i<=i-1; end 3: begin isdone<=1‘b1; i<=i+1; end 4: begin isdone<=1‘b0; i<=4‘d0; end endcase assign product=rp[16:1]; assign done_sig=isdone; endmodule例1.38 設被乘數M=0111(7),乘數Q=1101(-3),相乘過程如下:A為開始補加的零, A Q Q-1 0000 1101 0 初始值 1001 1101 0 A=A-M=0000-0111=1001 1100 1110 1 右移(第1次循環)/2 0011 1110 1 A=A + M=1100+0111=0011 0001 1111 0 右移(第2次循環)/2 1010 1111 0 A=A-M=0001-0111=1010 1101 0111 1 右移(第3次循環)/2 1110 1011 1 右移(第4次循環)/2 乘積=11101011=(-21)(十進制) 其中的移位是算數移位. 被乘數n位要移位3次.
verilog乘法器的設計
