題目描述-->p2700 逐個擊破

題意概括

花費最小的代價,使得一些有標記的節點不連通.

分析

我們需要花費最小代價使得原來連通的圖中一些節點之間不相互連通.

貪心顯然是可行的(一點也不顯然

看到其他人寫了dp,寫了貪心.

但我感覺可以排序+並查集做啊.

排序

考慮我們要花費最小代價刪邊,但是並查集不支持刪除操作.

(貌似有一種東西叫分治線段樹可以維護這種操作.

因此,我們根據容斥原理(這玩意是叫容斥吧.

花費最小代價刪邊,等價於花最大代價建邊,最後剩下不建的邊,就是我們的答案.

所以說,我們需要按照邊權從大到小建圖。sort！

我們需要保證的是兩個敵人節點不互相連通.

這就是我們並查集的作用!

並查集

首先明確：

並查集要初始化,一定要初始化!

下面的圖中,紅色代表敵人節點,綠色代表我方節點.

如果某兩個節點是我們的敵人節點,我們一定不會去建邊.(為虎作倀? 像這樣↓.

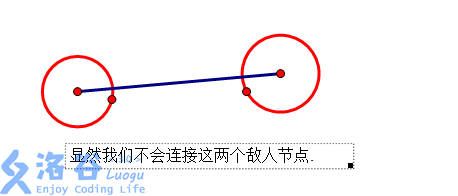
如果你連接,那你就違背了題目要求,你也不是一個

秉承偉大軍事家的戰略思想，一個有智慧的軍長了

還有,如果我們已經將敵人包圍建出下面這樣的圖這時,還有一個敵人節點.↓

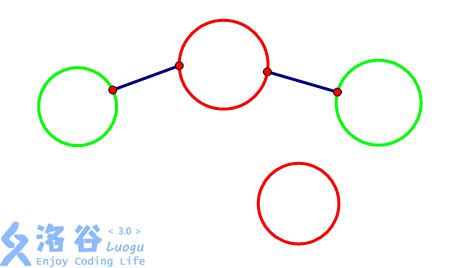
如果我們連接某一個我方節點,不連接敵方節點,那敵人也會互相連接(翻過屋後的山

所以說我們需要考慮一下如何解決這種情況.

如果,我方節點已經連接了敵方節點,則需要標記我方節點,使得敵方節點無法通過我方節點連接敵方節點.

因此說,我們可以把連接到敵人節點的我方節點變成敵人節點.

從而使得其他敵人節點與其無法連接.

那我們上面的圖就變成這樣↓

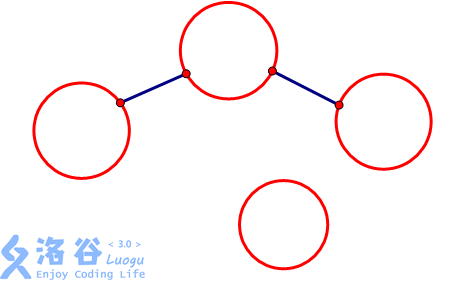
這樣我們的程序就可以實現我們所想了.

最後我們會將邊權大的邊加入到並查集中.

則最後沒有加入到並查集中的點,就會是被孤立的敵方節點.

所以我們把總邊權減去我們加入到圖中的邊權就是我們的ans啦！

關於樣例

樣例建的原圖↓

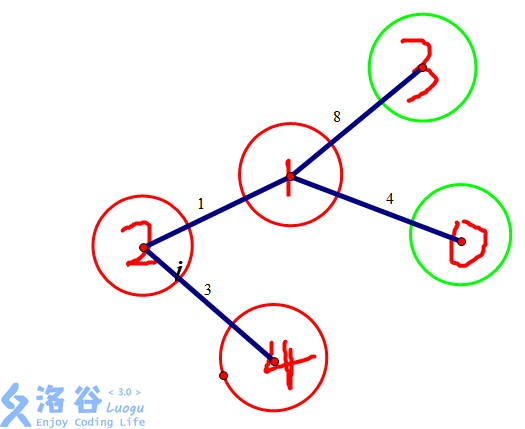
最終是這樣的↓

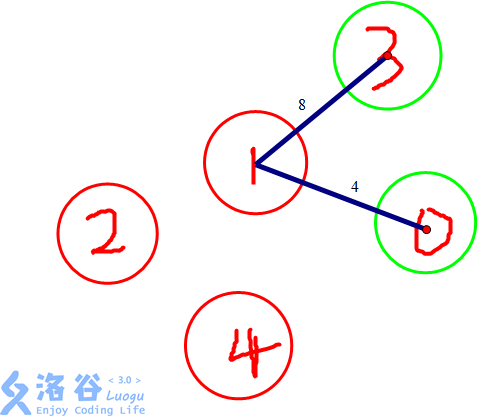
因此我們在樣例的答案是4.

--------------------代碼---------------------

#include<bits/stdc++.h>
#define IL inline
#define RI register int
IL void in(int &x)
{
    int f=1;x=0;char s=getchar();
    while(s>‘9‘ or s<‘0‘){if(s==‘-‘)f=-1;s=getchar();}
    while(s>=‘0‘ and s<=‘9‘){x=x*10+s-‘0‘;s=getchar();}
    x*=f;
}
int n,k,f[100008],tot;
bool init[1000008];
long long ans;
struct cod{int u,v,w;}edge[100008];
IL int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
IL bool ccp(const cod&a,const cod&b){return a.w>b.w;}
int main(void)
{
    in(n),in(k);
    for(RI i=1;i<=n;i++)f[i]=i;//一定要初始化!
    for(RI i=1,x;i<=k;i++)in(x),init[x]=true;
    for(RI i=1;i<=n-1;i++)
        in(edge[i].u),in(edge[i].v),in(edge[i].w),ans+=edge[i].w;
    std::sort(edge+1,edge+n,ccp);//從大到小sort.
    for(RI i=1;i<=n-1;i++)
    {
        int u=edge[i].u,v=edge[i].v,w=edge[i].w;
        int fu=find(u),fv=find(v);
        if(init[fu] and init[fv])continue;
        f[fu]=fv;
        ans-=w;//減去邊
        if(init[fu])init[fv]=true;
        else if(init[fv])init[fu]=true;
    }
    printf("%lld",ans);
}
 

p2700 逐個擊破